Развитие теории программ и систем в СССР: История и современные теории
Лаврищева Екатерина Михайловна
Введение
Более двадцати лет назад А.П. Ершов писал, что теоретическое программирование является разделом математической науки, объектом изучения которой является абстрактная программа, выраженная логической структурой и информацией, подлежащая выполнению на компьютере. Теория программирования основывается на математических дисциплинах (логика, алгебра, комбинаторика) и отражает математический метод мышления специалиста при проведении анализа предметной области, осмыслении постановок задач, описании программ для получения на машине математического результата. Теория программирования ориентирована на специалистов, обладающих математическими знаниями и способностью применять их к логике описания алгоритмов программ.
На начальном этапе создания ЭВМ в СССР сформировались теории построения программ (А.А. Ляпунова, А.П. Ершова, Ю.И. Янова, Е.Л. Ющенко, Э.Х. Тыугу, Г. Буча, К. Джекобсона и др.) и систем АС, АСУ, АСНИ, АСУ ТП (В.М.Глушкова) [1-9]. Системы разрабатывались с помощью готовых элементов – программ и модулей, которые накапливались в Фондах алгоритмов и программ (1976-1992), а позднее в библиотеках и репозиториях систем международного сообщества.
Модулем считался программный элемент, который преобразует множество исходных данных X во множество выходных данных Y методом отображения M: X → Y. Система из модулей - это пара S = (T, χ), где Т – модель системы; χ – характеристическая функция, определяется на множестве вершин X графа модулей G. Две модульные системы S1 = (Т1, χ1) и S2 = (Т2, χ2) тождественны, если Т1 = Т2 и χ1 = χ2, а S1 и S2 являются изоморфными, если Т1 изоморфна Т2 и χ1 = χ2 [10].
Процесс разработки программ и систем из модулей
постепенно становился регламентированным с помощью моделей жизненного цикла
(ЖЦ) (водопадная, спиральная, интеграционная и др.) и стандартов ISO/IEC 12207
Life Cycle 1996 (2007), ISO/IEC 11404 – GDT 2007, ISO/IEC 9000 Quality SW и др.
За рубежом сформировались новые формальные методы спецификации программ (VDM,
RSL, Z, B и др.) [11, 12] и их доказательства (Флойд, Хоар, Дейкстра, Грисс и
др.) [39, 40]. После модуля новым элементом программирования стал объект в ООП
Г.Буча [13] и связанные с ним такие математические понятия, как класс,
наследование, полиморфизм, инкапсуляция и др. Разработаны CASE-средства
моделирования объектных систем (Rational Rose, UML, MDA, MDD, PIM, PSM, SOA и
др.) [21].
Системы разрабатывались на основе характеристических моделей и готовых программных ресурсов (объектов, компонентов, сервисов и др.). Первые вариабельные модели систем и продуктов определены в Product Line/Product Family, GDM, Grid и др. [17-19]. Их основу составляет модель характеристик (Feature Model) и конфигурационная модель (CM) для сборки базовых артефактов и готовых ресурсов (reuses, assets, services и др.). В рамках Software Engineering Methods and Theory (SEMAT-2009) дана классификация дисциплин SE [20] и предложены перспективные теории и методы определения научных основ программирования для повышения уровня знаний и компетенции специалистов и магистрантов ВУЗов, готовящихся к производству программных, информационных и прикладных систем (http://www.semat.org).
В данной работе дается краткое описание первых теорий программ и систем и новых перспективных теорий математического моделирования систем из готовых ресурсов.
1. История развития теории программ и систем в СССР
1.1. Первые теории программ и программных технологий
Теория программ (по А.П. Ершову) образует новый раздел математической науки, объектом изучения которой являются математические абстракции программ, предписания, выраженные на специальных языках с заданной информационной и логической структурой для исполнения на ЭВМ. Основу теории составляла схема программы, которую впервые ввел А.А. Ляпунов и которую развивали Ю.И. Янов, А.П. Ершов и др. [1-9].
Схема программы – это конечный ориентированный граф, описывающий схему связи отдельных функций программ с помощью сигнатур операций и математических символов.
Схема Янова – это модель операторной схемы на сигнатуре одноместных операций, допускающих использовать одну переменную. Для схемы определена полная система преобразований, отображенная в протоколе последовательности выполняемых операций и значений их переменных.
Андрей Петрович Ершов развил понятие схемы программы и сформулировал идею сведения вычислимой функции к понятию детерминанта, инвариантного к различным способам задания процесса вычисления программ. Автомат, воспринимающий этот детерминант, рассматривается как конечный автомат, допускающий формальную эквивалентность, совпадающую с функциональной интерпретацией алгоритма программы. Формальная нотация программ дается в лексиконе и содержит описание семантики в виде совокупности нетривиальных фактов о вычисляемых ею функциях. Теория схем программ и вычислимости алгоритмов развивалась учениками Ершова и др.
А.П. Ершов в докладе на звание академика СССР (1986) и на Всесоюзной конференции «Технология программирования» (1987) [22, 23] определил элементы теории технологии программирования (ТП), включая методы синтеза, сборки и конкретизации. Синтезирующее программирование базируется на методе доказательного рассуждения о правильности программы. Сборочное программирование осуществляет построение программы из уже существующих (проверенных на правильность) готовых фрагментов программ (reuses) и сборку их в сложную структуру. Конкретизирующее программирование обеспечивает построение системы по универсальной модели для некоторой предметной области.
Основные положения теории ТП А.П. Ершов сформулировал так [23].
«Следует различать ТП как технологическую теорию и как конкретный способ организации, создания, распространения и сопровождения программного продукта (ПП) и как процедуру индивидуальной деятельности профессионала, разрабатывающего ПП. Технология и методология – это всегда наука, в то время как метод входит в них составной частью. Технология профессионального, производственного программирования имеет принципиальную важность - отчуждаемость и тиражирование ПП. Технология начинается тогда, когда она охватывает ЖЦ ПП. ТП – это совокупность методологических положений, организационно-административных и инструментально-технических средств, их информационного и программного обеспечения (ПО), регламентирующего деятельность людей, вовлеченных в процесс создания, распространения и сопровождения ПП. Конечная ТП должна:
- охватывать весь жизненный цикл ПП;
- способствовать применению методологии, повышающей уровень достоверности, надежности и доказательности программирования на современные технические средства в виде автоматизированных рабочих мест, объединенных в локальную сеть;
- обеспечивать управляемость и контролируемость производственных процессов;
- обеспечивать устойчивость ПП по отношению к смене технических средств;
- обеспечивать развитие ПП в связи с изменением условий функционирования целевой системы, использующий этот продукт в других условиях среды».
Таким образом, А.П. Ершов сделал ориентир для развития ТП в советских условиях. В [23] определено три направления развития ТП и ее перспективы.
«Первое направление (организационное программирование) 1975–1985 гг.
Язык программирования не формализован. Переход от прототипа к программной версии не формализован…
Языки программирования – ФОРТРАН, КОБОЛ, ПЛ/1, Ассемблер.
База знаний отсутствует, развитие продукта – версионное.
Второе направление (сборочное программирование) 1985–1995 гг.
Язык спецификации регламентирован.
Переход от прототипа к промышленной версии регламентирован. Язык разработки – этот формализованный язык высокого уровня со средствами модуляризации и комплексирования …».
Третье направление (доказательное программирование) 1995–2005 гг.
Язык разработки формализован и содержит систему формальных преобразований, необходимых для доказательства программ…
Язык программирования объединен с языком разработки…
База данных проекта машинизирована.
Развитие продукта – эволюционное – адаптивное…».
В заключительной части статьи А.П. Ершов отметил: «Было бы полезно выработать норматив по технологии второго поколения, который, не затрагивая конкретного методологического или языкового наполнения, унифицировал бы: общую этапность разработки ПП; нормативы производительности и надежности; документационную структуру и вычислительную среду; межмодульный интерфейс поддержки сборочного программирования…».
Все указанные фундаментальные основы ТП Ершова развивались в СССР в работах автора до 2016 года [24-27].
Впоследствии метод сборки модулей и интерфейсов (1982) [16, 24-27] стал всеобщим для всех общесистемных сред (IBM, MS, Intel, Linux и др.) и был определен как стандарт конфигурационной сборки - ISO/IEC JTC 1/SC-7 Configuration и др.
Следует отметить, что была разработана система программирования ПРИЗ (Э.Х. Тыугу) для синтеза программ на основе семантической модели предметной области и описания отдельных программ в PL/1, Fortran, Assembler и др. Метод синтеза реализован путем подстановки семантики их реализации в синтезируемую программу. (Кахро М.И., Тыугу Э.Х. Инструментальная система программирования на ЕС ЭВМ (ПРИЗ) – Финансы и статистика, 1981; Тыугу Э.Х. Концептуальное программирование – Наука, 1984).
Композиция программ (Редько В.Н.) – это операции объединения функций и данных типа: «данные–функция–имя» и «функции-композиция-дескрипция» на множестве именованных данных, дескрипций и денотатов (значений). Операции композиции – это подкласс стандартных композиций и композиционных функций. Они обеспечивают композицию функций на уровне ЯП. (Редько В.Н. Композиции программ и композиционное программирование // Программирование. – 1978. – № 5. –с. 17– 26).
1.2 Теория дискретных систем
Дискретные преобразователи
Другим видом теории программирования является теория алгебраического и алгоритмического программирования (В.М. Глушков), основанная на алгебраическом математическом аппарате для задания операций над элементами программ.
Академик Виктор Михайлович Глушков развил аппарат операторных схем программ в направлении теории эквивалентности дискретных преобразователей компьютеров. Основу этой теории составляет: χ – конечный автомат Мили с входным алфавитом X и выходным алфавитом Y, с заданными начальным и заключительным состояниями. В.М. Глушковым рассмотрен автомат Мура Gm (бесконечный) с множествами состояний G, входов X, выходов Y, начальным состоянием е, функцией выхода m(g) и функцией перехода q(g, y) = gy [3, 28-32].
Автомат χ, работающий совместно с Gm, получил название дискретного преобразователя. Если автомат χ в качестве входа воспринимает выход Gm, то в качестве выхода определен χ. Выходу автомата χ соответствует состояние Gm в момент остановки χ. Дискретные преобразователи эквивалентны относительно полугруппы G, если для каждого отображения m из G в Y оба не останавливаются при работе Gm либо оба останавливаются и имеют одинаковый выход.
Проблема эквивалентности дискретных преобразователей разрешима относительно полугруппы с левым сокращением и неразрешимой единицей, в которой разрешима проблема тождества слов. В ней допускаются все разрешимые и неразрешимые случаи эквивалентности дискретных преобразователей относительно коммутативной полугруппы. Данная теория применялась при построении серии машин Мир 1-3 [31].
Теория дискретных систем
При решении сложных математических задач дискретных систем возник новый общематематический язык, получивший название концепторного языка (КЯ) [33, 34]. Он позволял давать формальное описание: суммирования бесконечных рядов, выполнять множественные операции с бесконечными множествами, гильбертов оператор и др. КЯ – это многосортный логико-математический язык выражений Х, задаваемых с помощью объектов и типов. Тип – это средство построения выражений и структуризации множества значений денотатов. Выражение состоят из термов и формул. Термы – это объекты предметной области, а формулы – это утверждения об объектах и отношениях между ними. Формулы описываются с помощью четырех категорий понятий: функторов, предикатов, конекторов и субнекторов.
Функтор – это конструктор, преобразующий термы в термы (арифметические и алгебраические операции над числовыми множествами).
Предикаты превращают термы в формулы.
Конекторы включают в себя логические связи и кванторы для преобразования одной формулы в другую.
Субнектор (дескриптор) – это конструктор формул из термов и выражений, которые содержат формулы над числовыми множествами и вещественными функциями (кортежи, отношения, семейства, произведения множеств и др.).
В КЯ практически задавалась логико-алгебраическая спецификация задач распознавания динамических обстановок в гидроакустике, радиолокации и других дискретных систем. В частности КЯ использовался при создании ПО технических объектов новой техники. Дискретная система (S) содержит конечный набор входов, выходов и состояний. Ее функционирование определяется набором частичных отображений, которые входят в состав сигнатуры и образуют частичную алгебру состояния S системы. Если спецификации заменить булевыми функциями, то получается характеристическая функция отношений. Семантика логико-алгебраических спецификаций КЯ основана на переписывании термов и теории доказательства теорем. Данный язык использовался при разработке новой машины «Украина» в ИК АН СССР в 80-х годах ХХ столетия.
Алгебра алгоритмов
В.М. Глушков (1957-1964) определил алгебру и математический анализ как средство моделирования параметров и свойств программы решения дифференциальных и интегральных уравнений и систем [28-32]. Основу алгебры составляли:
- физическая модель, включающая свойства и характеристики отдельных элементов;
- математическая модель, в которой уточнялись размерность, параметры и операции работы с данными;
- формальное описание математической модели и численной модели;
- описание математических задач с помощью Адресного языка [32] и языка Аналитик [31], которые включали математические операции (+, х, ⋃, ∩, /, ◊, ⊕, – … ), десятичные исла, рациональные числа и операции тождественных преобразований.
Утверждение: если выражения Q1 и Q2 принадлежат некоторой подалгебре Q, в которой задана каноническая форма F и F(Q1) и F(Q2) полностью совпадают, то Q1 и Q2 – эквивалентны.
Язык Аналитик – это язык математического моделирования инженерных задач на машинах серии Мир1-3 [31]. Описание инженерных и математических задач проводится с помощью математических операций и логических операторов, а также конструкций математического анализа и операции тождественного преобразования канонических форм с применением стандартных функций (тригонометрических, логарифмических, экспоненциальных и др.). В этом языке содержатся средства отладки, трассировки и выполнения численных задач вычислительной математики. В него вошли элементы адресного языка Е.Л. Ющенко (1957) [32], а именно операции теории множеств и отношений. Переменные обозначались буквами, им соответствовали ячейки машины. Содержимое некоторого адреса отмечалось указателем, адресом второго ранга (эта концепция вошла в зарубежные языки). Более всего этот язык применялся для описания программ трансляторов для машин УМШН, Урал, Днепр и др.
Развитием этого языка являются: универсальные алгебры (подалгебры, логики, многоосновные алгебры и др.); САА - системы алгоритмических алгебр (алгебра Поста, тождественные преобразования схем адресных алгоритмов), формальные языки и грамматики; теория синтеза автоматов, методы анализа и СМ-формализмы описания анализа языков программирования [30].
Теория информационных систем
В книге «Основы безбумажной информатики» (1982). В.М. Глушков определил для ИС, АСУ и АСУ ТП принципы [35, 36]:
- Системного подхода к анализу систем управления, структуризации и выделения их целей и критериев.
- Декомпозиции систем по функциональным признакам и свойствам подсистем разного назначения (кадрового обеспечения, делопроизводства, мониторинга, управления и т.п.).
- Моделирования элементов системы, типизации функций и задач системы, а также создания экономико-математической модели поиска проектных решений и построения вариантов системы.
- Добавления новых задач для улучшении деятельности организации, усовершенствования и введения новых функций управления. (мониторинг ИС, деловая графика, обмен электронными документами и т.п.).
- Определения внешних задач (анализ, учет, контроль) и внутренних (сбор, регистрация, хранение, поиск и др.) с целью принятия управленческих решений.
На основе сформулированных принципов строилась система электронного документооборота и управления правительством с учетом моделей документов, их размеров и характеристик.
Модель документов ИС [37]включает:
1). Характеристики объема, включающие регулярную часть из последовательности повторяемых групп полей данных и нерегулярную часть без повторяемых структур данных. Объем документов определялся по формулам:
- V=lh +nsks lsmax - средний;
- Vmax=lh+ nsmaxks lsmax - максимальный,
где lh – размер нерегулярной части документа; ns – количество строк данного типа документов; ks – коэффициент заполнения; lsmax – максимальный размер регулярной части документа.
2). Характеристики времени выполнения, включающие в себя:
- суммарные значения времени обработки разных типов документов в соответствии с их маршрутом;
- время выполнения отдельных операций над документами в разных узлах системы;
- время передачи документов между разными узлами ИС.
Данная теория апробирована в [37] и применяется в системе образования Украины.
Графический P-стиль описания программ
Р-стиль – это графическое описание процессов построения программ (Вельбицкий И.В.). Перевод графической Р-схемы программы в линейную форму записи для представления в ЭВМ осуществлялся соответствующими программами трансляторов комплекса РТК. Р-схемы изображались с помощью знаков >, -, | и буквы «о». Но так как в 70-годах прошлого столетия не было графических дисплеев, то описание схемы проводилось с помощью знаков алфавита, что затрудняло просмотр и их анализ. Технологические комплексы РТК созданы были на машинах БЭСМ-6, ЕС ЭВМ и СМ ЭВМ. Они использовались в различных организациях СССР для обработки текстовой информации и создания интерфейса с уже существующими программными системами. В рамках Единой системы программной документации (ЕСПД, ГОСТ 19) представлен стандарт ГОСТ на Р-технологию. Однако после распада СССР эти средства используются редко, так как не реализованы в классе новых компьютеров.
Теория модульных структур программ
Модуль – это элементарный программный элемент, имеющий свойства [10]:
- логической завершенности функции;
- независимости одного модуля от других;
- замены отдельного модуля без нарушения структуры программы;
- вызова других модулей и возврат данных вызвавшему модулю и др.
Модуль преобразует множество исходных данных X во множество выходных данных Y и задается в виде отображения M : X →Y.
Виды связи между модулями:
- связь по управлению (СР = К1 + К2);
- связь по данным.
Граф модульной структуры G = (X, Г), где X – конечное множество вершин, а Г – конечное подмножество прямого произведения Х х Х х Z на множестве дуг графа.
Модульной структурой называется пара S = (T, χ), где Т – модель модульной структуры; χ – характеристическая функция, определенная на множестве вершин X графа модулей G.
Значение функции χ определяется так:
χ(х) = 1, если модуль с вершиной х∈X включен в состав ПС;
χ(х) = 0, если модуль с вершиной х∈X не включен в состав ПС и к нему нет обращения из других модулей.
Определение 1. Две модели модульных структур Т1 = (Gl, Y1, F1) и Т2 = (G2, Y2, F2) тождественны, если G1 = G2, Y1 = Y2, F1 = F2. Модель Т1 изоморфна модели Т2, если G1 = G2 между множествами Y1 и Y2 существует изоморфизм φ, а для любого х∈X F2(x)=φ(f1(x)).
Определение 2. Две модульные структуры S1 = (Т1, χ1) и S2 = (Т2, χ2) тождественны, если Т1 = Т2, χ1 = χ2 и модульные структуры S1 и S2 изоморфны, если Т1 изоморфна Т2 и χ1 = χ2.
Модуль описывается в ЯП и имеет раздел описания паспорта, в котором задаются внешние и внутренние параметры. Для передачи параметров другому модулю используется оператор Call (...). Параметры могут преобразовываться к виду вызывающего модуля и обратно в случае неодинаковости их типов. Разработана библиотека примитивных функций преобразования разнородных типов данных ЯП [16].
1.3 Доказательство правильности программ
Формальное математическое доказательство программ основывается на спецификациях алгоритмов, аксиомах, утверждениях и условиях, называемых предусловия и постусловия, определяющих получение правильного результата некоторой специфицированной программой [38-41].
Предусловия – это ограничения на совокупности входных параметров и постусловий на выходных параметрах. Пред- и постусловие задаются предикатом, результатом которого будет булева величина (true/false). Предусловие истинно тогда, когда входные параметры входят в область допустимых значений данной функции. Постусловие задает формальное определение критерия правильности получения результата. Оно истинно тогда, когда совокупность значений удовлетворяет требованиям, задающим функциональность. Доказательство проводится с помощью набора утверждений для проверки правильности программ в заданных точках. Если утверждение соответствует конечному оператору программы, т.е. является заключительным утверждением и с помощью постусловия делается окончательный вывод о частичной или полной правильности программы.
Наиболее известные методы доказательства – это метод Флойда, Наура и др.
Метод рекурсивной индукции Флойда применяется для программ, которые разрабатываются путем декомпозиции задачи на несколько подзадач и для каждой из них формулируются утверждение с учетом условий ввода и вывода в точках программы, расположенных между входными и выходными утверждениями. Суть доказательства – это истинность выполнения условий и утверждений в заданной программе.
Метод структурной индукции Хоара основан на аксиоматическом описании семантики исходных программ в виде аксиом. Для каждой метки программы строится правило вывода, которое выводит полученные значения переменных.
Пример доказательства расположения элементов массива array Т[1:N] в порядке их возрастания в Т' [1:N] [10].
Входное условие задается начальным утверждением:
Анач: (Т [1:N] – массив целых) & (Т' [1:N] массив целых).
Выходное утверждение Акон - это конъюнкция (2, 3) условий:
(1) (Т– массив целых ) & (Т' – массив целых ),
(2) ∀i , если i ≤ N, то ∃ j (T'( i ) ≤ T' ( j )),
(3) ∀i , если i < N, то (T' ( i ) ≤ T' (i+1) ),
Если утверждение (1) - истинно, то истинно и (2). То есть,если (1) утверждение – А1 преобразуется к А2, то теоремой является: А1 → А2. Если А3 – следующая точка преобразования, то теоремой будет: А2 → А3 . И так до конца Анач→ Акон.
Конечная теорема формулируется так: условие истинно в последней точке, если оно отвечает истинности выходного утверждения: Анач→ Акон .
2. Современные теории и методы
2.1 Методы математической спецификации программ VDM, Z, CLEAR
Венский метод - VDM
К формальным методам спецификации относятся: Венский метод VDM D. Biorner, Z-метод (I.R. Abrial, B. Meyer), RSL и др. [12, 38]. Эти методы начали использоваться в реальных проектах, а также в университетских и академических организациях. VDM – язык формальной спецификации программ и данных с использованием математической символики и следующих типов данных: Х – натуральные числа с нулем, N – натуральные числа без нуля, Int – целые числа, Bool – булевы, Qout – строки символов, Token – знаки и специальные обозначения операций.
Функция в VDM задает определение свойств структур данных и операций над ними, аппликативно или императивно. В первом случае функция специфицируется через комбинацию других функций и базовых операций (через выражения), что соответствует синониму функциональный. Во втором случае значение определяется описанием алгоритма, что соответствует синониму алгоритмический. Например, спецификация функции вычисления минимального значения из двух переменных имеет вид: min N1 N2 → N3. Описание значения этой функции имеет вид: min (x, y) = if x < y then x else y.
Объекты языка VDM. Это элементы данных, которыми оперируют функции, которые могут образовывать множества, деревья, последовательности, отображения, а также формировать новые более крупные объекты.
Множество может быть конечное и обозначаться X-set. Используются операции ∈, ⊆, ⋃, ⋂ и др. для проверки правильности задания этих операций. Дистрибутивное объединение подмножеств имеет вид: union {(1, 2), (0, 2), (3, 1) } = (0, 1, 2, 3).
Списки (последовательности) – это цепочки элементов одинакового типа из множества Х. Операция len задает длину списка, а inds – номер элемента списка. Могут использоваться также операция конкатенации и дистрибутивной конкатенации.
Дерево – это конструкция mk, позволяющая объединять в комплекс объекты разной природы (последовательности, множества и отображения). Например, let mk – время (h, m) = t tin определяет значение h = 10, а m = 30.
Отображение – это конструкция map, позволяющая создавать абстрактную таблицу из двух столбцов: ключей и значений. Все объекты таблицы принадлежат одному типу данных – множеству.
При спецификации программ средствами VDM задаются пред- и постусловия, аксиомы и утверждения, необходимые для проведения доказательства правильности программы. Метод VDM ориентирован на пошаговую детализацию спецификации программ. Вначале строится грубая спецификация – модель программы в языке VDM, которая постепенно уточняется, пока не получится окончательный текст в ЯП.
Алгебраические спецификации языков Z, CLEA
Язык спецификации Z-схем задает описание обобщенной модели VM программы в виде узлов управления моделью; меток в узлах графовой модели; внешних характеристик и внешних параметров модулей модели. Эта модель представляется совокупностью Z-схем с набором деклараций и ограничений, способствующих образованию состояния. По этой модели осуществляется:
- выбор модулей из библиотеки шаблонов, их переименование и конкретизация в узлах графа;
- каждый модуль имеет интерфейс для некоторого порта, отмеченного меткой в Z-схеме;
- верификация связей модулей через описание интерфейсов;
- создание нового шаблона и его интерфейса для задания новых событий в схеме.
Интерфейс способствует образованию последовательности событий при наблюдении за поведением исполняемых модулей.
При спецификации модуля M проводится описание разных ситуаций, которые формируют конкретные события, их анализ и определение новых событий и условий выполнения событий.
Обобщенная модель VM состоит из двух модулей: модулей управления CONT и распределения памяти STOR и имеет вид: VM = (CONT || STOR) \ {reguest, response} = (coin → choc → VM)..
В нем модуль CONT задает следующую спецификацию:
CONT = ( coin → reguest → response → choc → cont)
Общее назначение этой спецификации состоит в том, чтобы потребитель мог вставлять данные в coin для отправки запроса (reguest ) модулю памяти. Этот модуль дает ответ (response) на запросы согласно следующей спецификации:
STOR = (reguest → response → stor ).
Модель VM определяет параллельную обработку модулей CONT, STOR, а также связь со средой обработки модели.
Спецификация CLEAR включает функции и отношения, которые задают поведение и отношение эквивалентности свойства объектов и операции над ними.
Особенностями таких спецификаций является наличие описаний функций, поддержка абстракции данных специальными средствами.
2.2. Теория оценки качества программ
Основным свойством военно-промышленных программ и программ бортовых систем являлась надежность и качество. Этим вопросам большое внимание уделял Владимир Васильевич Липаев. Он один из первых в СССР разработал методы обеспечения надежности и качества таких систем (Липаев В.В. Надежность программного обеспечения АСУ, Энергоиздат, 1981; Липаев В.В. Качество программного обеспечения, Финансы и статистика, 1983).
Под его руководством создан ГОСТ 2844-87 «Качество программных средств». В нем определена система управления качеством, включающая совокупность орга¬низационных методов управления процессом проектирования комплексов программ (КП) на этапах ЖЦ и методику учета технических показате¬лей качества в ходе ЖЦ для последующего их использования при оценке полученных показателей надежности и качества в соответствии с требованиями к ним.
Качество – это совокупность технических, технологических и эксплуатационных характеристик КП, которые входят в состав эталонной модели качества, представленной шестью базовыми характеристиками, значения которых могут быть определены количественно или качественно.
На этапах ЖЦ КП проводится контроль отдельных показателей качества специальной службой качества и устранение возникающих угроз качеству в связи с обнаруженными дефектами в КП. В задачи службы качества входит планирование и слежение за процессом достижения качества программ и систем на этапах ЖЦ, квалификационное тестирование, испытание пробной версии КП и оценка базовых показателей качества на основе собранных технических данных процесса проектирования КП.
После появления американских стандартов качества ISO/IEC 9000 (1-4) и ISO/IEC 9126 В.В. Липаев создает «Методическое пособие по программной инженерии» (2006) и учебное пособие «Программная инженерия сложных заказных программных продуктов» (2014).
В них описана методология проектирования качественных ПС с учетом стандартов ЖЦ ISO/IEC 12207-2007 и теории оценки качества. Эти пособия могут применяться при обучении курса «Программная инженерия».
2.3. Теория объектно-ориентированного проектирования Г. Буча
Г.Буч ввел новый стиль программирования, названный ООП [11, 13-16]. В нем определены базовые математические понятия - объект, класс, полиморфизм, наследование, изоморфизм и др. Объекты группируются в классы.
Класс - это множество объектов, имеющих общие переменные, структуру и поведение. Объект является экземпляром класса. Поведение экземпляра определяется операциями его создания, уничтожения и сериализации. Совокупность внешних переменных и методов класса определяет интерфейс, с помощью которого экземпляры классов взаимодействуют между собой. Для каждой внешней переменной существуют методы выбора значения (get-метод) и присвоение нового значение (set-метод). С общей точки зрения, интерфейс экземпляра объекта состоит из совокупности методов. Каждый объект может иметь сколько интерфейсов, которые определяют его функциональные свойства. Объект может иметь специальный интерфейс, методы которого работают с экземплярами (Home-интерфейс в модели EJB Java). То есть объект класса имеет: специальный интерфейс или один или несколько интерфейсов, которые реализуются в экземплярах компонентов. На абстрактном уровне интерфейс может рассматриваться как частичный вид класса.
Утверждение: Любой экземпляр определенного класса обладает всеми методами, которые определены в этом классе.
Экземпляр класса может быть приведен в соответствии с одним из суперклассов в соответствии с интерфейсом, который реализуется в этом классе.
Теория Г.Буча позволяет проектировать предметную область, исходя из утверждения, что весь материальный мир состоит из объектов. Любая предметная область – это совокупность объектов, связанных между собой некоторым множеством отношений и поведения в течение некоторого времени:
< объектная ориентация> = <обьекты> + <наследование>.
Каждое понятие предметной области, вместе с его свойствами и особенностями поведения является отдельным объектом, а вся область - это совокупность объектов со связями, которые устанавливаются на базе отношений между этими объектами. В качестве объекта выступают как абстрактные образы, так и конкретные физические предметы или группы предметов с указанными общими характеристиками и функциями.
Развитием ООП является UML [15]. В нем процесс построения системы проводится на этапе анализа предметной области и проектирования. В процессе анализа создается концептуальная объектная модель (ОМ) в виде диаграмм прецедентов. Она уточняет внешнее функциональное поведение системы. Создается каркас проектируемой системы. Для определения поведения классов объектов используются диаграммы состояний и деятельности. Размещение объектов в ОМ фиксируется компонентными диаграммами в узлах компьютеров сети, которые развертываются для выполнения.
Таким образом, теория Г. Буча - базис моделирования систем в UML [15], MDA, MDD, SOA и др. Она вошла в ЯП (С++, С,Basic, Java и др. ) [21].
2.4 Unified Modelling language
UML является языком проектирования систем с помощью визуальных диаграмм [15]:
- вариантов использования;
- классов;
- поведения, состояний, деятельности, взаимодействия;
- последовательности и кооперации;
- реализации (диаграммы компонентов и развертывания).
Размещение объектов в среде разработки задается компонентными диаграммами, а расположение программных модулей в узлах (компьютерах) сети — диаграммами развертывания.
Приведенные прецеденты (use case) или диаграммы применяются для проектирования следующих объектных моделей системы:
- структурная (статическая) модель, которая задает структуру понятий системы, включая классы, интерфейсы, отношения, атрибуты;
- модель поведения (динамическая), которая задает поведение объектов системы с помощью диаграмм взаимодействие и изменения состояний компонентов и системы;
- модель функционирования задает операции управления вычислением ПС.
Данные модели задаются в UML и реализуются Этот язык используется при создании современных систем и сайтов.
2.5. Теория моделирования систем из готовых ресурсов
Моделирование основывается на математических операциях построения моделей систем и модели MF, отображающих функциональные свойства элементов системы и возможность их изменять, удалять и заменять новыми. Элементы модели MF могут отмечаться точками вариантности для формирования версий систем в семействе систем и доказательства архитектуры системы средствами математического аппарата матриц смежности и достижимости [10, 14-19].
Теория моделирования изменяемых систем и их семейств основывается на конфигурационной сборке готовых ПП фирмы SEI (Product Lines/ProductFamilies) и теории управления вариантами систем с учетом требований заказчика. На основе этой теории проводится анализ моделей действующих операционных систем (Linux, Intel и др.), систем реального времени и моделей Веб-систем (SOA, SCA) путем извлечения базовых элементов и генерации вариантов ОС и Веб-систем. Разработаны методы верификации, трансформации и Variability Minning готовых Legacy Systems. Для описания интерфейсов отдельных элементов системы предложены языки IDL, SDL и др., позволяющие производить отображение неэквивалентных сложных данных к более простым данным. Эти механизмы составляют фундамент трансформации неструктурированных видов данных в современных Больших хранилищах (Big Data) и решения задач в Cloud Computing [21].
При создании ИС и ПС используются методы генерации готовых ресурсов (reuses, services, assets, artifacts, objects, components и др.), накопленных во многих библиотеках реализаций и интерфейсов серверов Интернет в языках IDL и WSDL стандарта WWW3C. Разнородные готовые ресурсы методом конфигурационной сборки объединяются в требуемые варианты систем и семейств систем для решения конкретных задач предметной области.
2.6. Базовые основы программной инженерии
Программная инженерия (Software Engineering – SE, 1968) – это систематический подход к разработке, эксплуатации, сопровождению и прекращению использования программных средств (www.swebok.com). Ядро SWEBOK (Software Engineering Body of Rnowledge) разработан международным комитетами ASM и IEEE и предназначен для обучения программной инженерии – Curricula 2001 (2004, 2007, 20014). В состав SE входят методы, средства и инструменты, которые обеспечивают качественный и производительней труд программистов при создании ПО и ПС [10, 13-19, 44].
Появлению термина ПИ в СССР предшествовал термин технология пpoграммирования, который обозначал методы, средства и инструменты, обеспечивающие процесс создания ПС. Эти определения настолько близки, что фактически ПИ можно трактовать как дальнейшее развитие ТП в плане обеспечения программистского труда инженерными методами (планирование, учёт, контроль). Такое развитие, по существу, означает переход от одиночного создания программ отдельными лицами к промышленному их производству.
В SE разработан стандарт ЖЦ ISO/IEC 12207-1996, 2007 для регламентации процессов разработки ПП с заданными свойствами (функциями и качеством). В сфере SE существуют другие виды работ: копирование программ и документации; настройка и генерация программ; ввод и контроль данных и др. Эти виды работ наиболее близки к производству. Многие из них стандартизированы. Применяются также специализированные операции (отладка, верификация, тестирование и др.) в рамках стандарта ISO/IEC 12207. Они могут выполняться в соответствии с технологией создания ПО, основу которой составляет ядро SWEBOK с 10 областями знаний, которые задают наколенные знания в области реализации ПО различного назначения.
Для управления качеством ПП создан стандарт ISO/IEC 2844–89 «Оценка качества программных средств» (1987). Он предусматривает большой объем рутинных работ по оценки отдельных свойств и характеристик ПС с учетом 50 критериев и 6 факторов стандарта измерения качественных и количественных показателей ПО систем.
Новые дисциплины программной инженерии
Сформулированы (2008) новые дисциплин Software Engineering (рис.1) [16, 20, 41]:
- научное программирование – совокупность теоретических и формальных основ программирования и автоматизации проектирования разных программных и прикладных систем;
- инженерная дисциплина – совокупность средств и методов проектирования на основе ЖЦ стандарта отдельных приложений систем, их тестирования и оценки качества выходного кода, интероперабельного до платформ и сред;
- дисциплина управления – методы управления и организации планирования работ по изготовлению коллективом отдельных элементов систем, анализа рисков срыва планов, верификации и генерации варианта продукта;
- экономическая дисциплина – совокупность методов экспертного, качественного и количественного оценивания результатов создания с необходимыми расчетами общего времени, объема, трудоемкости и стоимости изготовления готового продукта;
- индустриальная дисциплина – это промышленная технология конвейерного сборочного производства систем из готовых программных ресурсов (КПИ, ГОР) из библиотек и репозиториев по заказу продукта пользователем;
- дисциплина обучения SE по международным программам Education -2000, 2010, 2025 (http://www.teachingbox, http://www.microsoft.com и др.), а также обучения SE на отечественном сайте http://7dragons.ru/ru.
Данные дисциплины вошли в Международные программе обучения - Curricula SE and Computer Science (2007, 2013).
SEMAT – Software Engineering Methods and Theory (2009)
В SEMAT (I. Jacobson, B. Мeyеr и Р. Soley) поставлена цель – развивать SE так, чтобы разработка ПО квалифицировалась как строгая математическая дисциплина (идея, близкая идеи А.П.Ершова 1986 [22, 23]. Цель состоит в том, чтобы продолжить многолетнюю работу по созданию теории и методов SE и преодолеть разрыв между теорией академических специалистов и сообществом разработчиков конкретных видов ПО. Работы в SEMAT структурированы по четырем областям: Практика, Образование, Теория и Сообщество.
Практика развивает прикладные и практические работы. Образование затрагивает вопросы, связанные с обучением разработчиков, студентов и специалистов ПО. Теория занимается созданием общей теории для разработки ПО и систем. Сообщество - это специалисты, которые создают веб-сайты и развивают их для потребностей пользователей. Со временем Практика, Образование и Теория будут интегрироваться. Теория должна будет направлять исследования и создавать научные теории в SE для разработчиков ПО. Образование должно внедрять новые теории при преподавании в ВУЗах. В SEMAT будут разработаны новые теории применительно к системам на кластерах и суперкомпьютерах.
2.7. Новый объектно-компонентный метод (ОКМ)
ОКМ создан для логико-математического моделирования систем на четырех уровнях (обобщенном, структурном, характеристическом и поведенческом) [26, 27, 41-45]. Каждый уровень позволяет детализировать и уточнять объекты системы в виде графа и их отношений на множестве объектов предметной области с постепенным уточнением их денотатов и концептов по теории Фреге и их отображением в модели MF. Задание структуры системы и действий над объектами (объединение, удаление, замена и др.) осуществляется с помощью математических и логических операций (È, Ç, /, à, Å , –, &, V…). На первом уровне проводится декомпозиция предметной области системы с помощью объектов. На следующих уровнях определяются их внешние характеристики MF и создается графовая ОМ G (рис.1), в вершинах которой находятся объекты, а дуги задают их интерфейс для передачи данных между ними. На последнем уровне проектирования для объектов определяется поведение их функций в определенной среде.
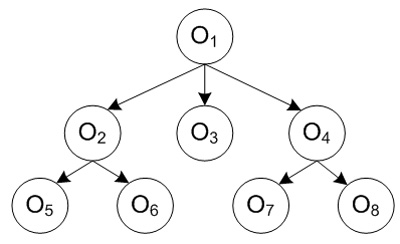
Рис.1. Структурный граф G
Граф ОМ обладает свойствами:
- вершины графа задают взаимно однозначное отображение на множества объектов;
- каждая вершина имеет хотя бы одну связь с другими вершинами графа;
- существует одна вершина О1 графа G, которая отображает предметную область в целом.
Построенный граф G корректируется, реструктурируется с помощью новых объектов и интерфейсов и получается расширенный граф.
Таким образом, формируется граф G ={О, I, R}, в котором О — множество объектов (функций); I - множество интерфейсов и отношений R (relations, заданных стрелками на графе) между объектами (рис.2).
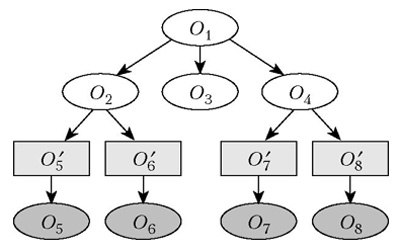
Рис.2. Граф G на множестве объектов и интерфейсов
Объекты расширенного графа G переводятся к программным компонентам, которые погружаются в компонентную среду. Объекты и компоненты этих моделей собираются в репозитории компонентной среды и могут конфигурироваться в разные варианты ПП ПС.
В вершинах графа G находятся функциональные объекты — О1, О2, О3, О4, О5, О6, О7, О8 и интерфейсные объекты — 0’5, O’6, O’7, O’8 . Все объекты размещаются в репозитории, а дуги соответствуют отношениям между всеми видами объектов. Элементы графа О1—О8 описываются в ЯП, а интерфейсные объекты O’5—O’8 в языке IDL (Interface Definition Language). Параметры внешних характеристик интерфейсных объектов передаются между объектами через интерфейсы и помечаются в них in (входной), out (выходной), inout (входной и выходной) в языке IDL.
Для графа G на рис. 2 сформирован набор программ P0 — P5 , заданных с помощью математической операции объединения (сборки) link:
- P1 = О2 ⋃ О5 , link P1 =In O’5 (О2 ⋃ О5);
- P2 = О2 ⋃ О6, link P2 =In O’6 (О2 ⋃ О8);
- P3 ;
- P4 = О4 ⋃ О7, link P4 =In O’7 (О4 ⋃ О7);
- P5 = О4 ⋃ О8, link P4 =In O’8 (О4 ⋃ О8);
- P0 = (P1 ⋃ P2 ⋃ P3 ⋃ P4⋃ P5).
Результатом связи двух объектов графа (например, 025 и 047) является интерфейсный объект O’5 , O’7 в котором множество входных интерфейсов совпадает с множеством интерфейсов объекта-приемника, а множество исходных интерфейсов — с множеством исходных интерфейсов объекта-передатчика.
Аксиома. Расширенный граф G с интерфейсными объектами струк¬турно упорядочен (наверх), проконтролирован на полноту, избыточность и отсутствие дублирующих элементов.
Модель вариабельности и конфигурации
Объекты графа G образуют модель системы, по которой проводится конфигурация системы. Измененяемые элементы графа помечаются точками вариантности (или вариабельности) [26, 27].
Точка вариантности – место в модели системы ПС, с помощью которой осуществляется выбор варианта системы. По этим точкам задаются варианты системы. Точки вариантности обрабатываются конфигуратором и позволяет трансформировать готовую систему путем замены одних используемых компонентов повторного использования (КПИ) другими, более функциональными или корректными.
Вариабельность – свойство продукта (системы) к расширению, изменению, приспособлению или конфигурированию с целью использования в определенном контексте и обеспечения последующей его эволюции ( ISO/IEC FDIS 24765- 2009 (E).
Модели с вариабельными элементами используется при конфигурации продукта (Product Configuration) из готовых КПИ или взятых из библиотек reuses.
Модель вариабельности ПС:
MFvar = (SV, AV), где
SV – подмодель вариабельности артефактов структуры ПС;
AV – подмодель вариабельности разработанного продукта ПС.
Модель MFvar обеспечивает уровень изменяемости артефактов и продуктов ПС, снижает затраты и уменьшает сроки разработки продукта ПС.
Подмодель SV = ((Gt, TRt ), Con, Dep),
где Gt = (Ft, LFt ) – граф артефактов типа t (требования, компоненты, тесты и др.);
TRt – двусторонние связи артефактов типа t;
Con і Dep – предикаты на декартовом произведении множеств артефактов, которые задают ограничения и зависимости между функциями и показателями качества ПС.
Подмодель AV определяет структуру ПС из КПИ, которые имеют паспорта и сохраняются в репозитории. Подмодель SV отображает функциональные и вариантные характеристики КПИ и продукта, а также аспекты отношения между ними.
Модель SV конкретизируется в линию разработки и сборки в ПС.
Приведенные модели используют артефакты (reuses, object, services, components), которые трансформируются к программному виду с помощью модели конфигурации [21] вида:
Мkonf = (ОМ, MПрО , Мпс, MFvar , Mвз),
где Mвз – модель взаимодействия отдельных элементов создаваемой системы.
На основании модели Мkonf осуществляется:
- подбор артефактов и ресурсов ПС в базе конфигурации заданной системы;
- выделение общих и вариантных характеристик ПС в модели FM и модели ПС;
- планирование многократного использования ресурсов для ПС в точках вариантности и их фиксация для их удаления или замены;
- сборка ресурсов в ПС и их адаптация к новым условиям среды функционирования;
- управление вариантами ПС с заменой отдельных функций в ПС;
- управление взаимодействием артефактов в гетерогенной среде.
Метод ОКМ представлен на сайте http://7dragons.ru/ru. Базу данных сайта образует репозиторий готовых ресурсов, модели ПС, вариабельности и взаимодействия общесистемных средств - Visual Studio, Eclipse, CORBA, WSphere [46, 47]:
- Visual Studio.Net«Eclipse определяет среду взаимодействия отдельных элементов в языке С# и интерфейса. Модель устанавливает связь элементов с заданной средой через конфигурационный файл.
- CORBA«JAVA«MS.Net обеспечивает связь между этими средами с помощью заданных в этих языках элементов с целью доступа к ним других разработчиков.
- IBM WSphere«Eclipse обеспечивает связь между программами в ЯП этих сред.
Верификация и тестирование вариабельных систем
Вариабельность модели MF может быть проверена на правильность с помощью решателей и инструментов автоматического доказательства различных видов моделей (SAT, BDD и пр.), описанных в формальных языках Alloy, B или Ζ [21, 41], а также с помощью Model Checking, применимой к модели MF с конечным числом состояний, описанных с помощью формальных спецификаций. При этом в методе Крипке модель MF формально задается в виде: M = (S, S0, R, L), где S — множество состояний, S0 — множество начальных состояний, R — отношение переходов, L : S → 2 AP
x0 — функция разметки. Эта модель описывается с помощью языка темпоральной логики с помощью утверждений, истинность которых проверяется верификацией. Подход в ограничениях (Constraint Satisfaction Problem) применяется к модели вариабельности, если в ней заданы условия выполнения в ограничениях . Еще одним способом верификации являются онтология, основанная на трансляции модели вариабельности MF в модель онтологии, описанной в языке OWL DL (Ontology Web Language Description Logic). После трансляции описания в этом языке используется автоматизированный инструмент RACER [45].
Тестирование готового продукта, созданного методом конфигурирования, проводится с помощью набора тестов для отдельных элементов ПП. Метод Дж. МакГрегора (McGregor) [48] «от требований» (requirements-based testing) проводится с помощью тестов, проверяющих функциональные и интерфейсные объекты. В качестве инструмента тестирования используется фреймворк Visual Studio 2010 со средствами проверки правильности тестирования разных видов объектов. В него входит компонент Test Manager, который управляет средствами планирования процесса тестирования и выполнения тестовых сценариев. Обращение к фреймворку тестирования производит сайт http://7dragons.ru. При обнаружении ошибок в процессе тестирования вносятся исправления в модели MF и ПС. Затем проводится повторное конфигурирование и получение ПП с добавлением новых объектов или удаления старых.
Заключение
Рассмотрены формальные основы теории и технологии программирования в начальный период развития вычислительной техники в СССР и в последующие годы. Дан обзор основ теории программ Ляпунова, Ершова, Глушкова, Дейкстры, Бьорнера, Буча, Лаврищевой и др. Представлена сущность теории программ, методов разработки и доказательства программ, а также технологии программирования модулей в ЯП и инженерных методов создания ПП в Software Engineering и SEMAT. Определено математическое проектирование систем из готовых ресурсов (объектов, компонентов, сервисов и др.) в ОКМ и рассмотрены модели вариабельности, взаимодействия и конфигурирования систем из этих ресурсов. Определен формальный аппарат трансформации элементов ОМ к компонентной модели с учетом модели вариабельности и взаимодействия, а также реализована конфигурационная сборка готовых элементов заданных моделей и приведения их к выходному коду на сайте http://www.ispras.ru/lavrischeva/7dragons.ru/ru.
Литература
- Янов Ю. И. Схемотология программ. - "Проблемы кибернетики", 1958, в. 1, с. 75-127;
Ляпунов А. А. Схемы программ. - "Проблемы кибернетики", 1958, в. 1, с. 46-74.
Глушков В. М., Летичевский А. А. в кн.: Избранные вопросы алгебры и логики, Новое издание, 1973, с. 5-39;
Ершов А. П. Введение в теоретическое программирование М., 1977.
Котов В. Е. Введение в теорию схем программ, Новосибирск, 1978.
Непейвода Н. Н. Логика программ. - Программирование, 1979, М 1, с.15-25;
Скотт Д. "Кибернетический сборник", 1977, в. 14, с.107-21;
Семантика языков программирования. Сб. статей, пер. с англ., М., 1980;
Manna Z. Mathematical theory of computation, N.Y., - [а. <о.], 1974.
Лаврищева. М. Методы программирования. Теория, Инженерия, Практика. – Наук.Думка. –2006. –451с.
Грис Д. Наука программирования. – М.: Мир. –1984.
Biorner D., Jones C.B. The Vienna Development Methods (VDM): The Meta– Language.– Vol. 61 of Lecture Notes in Computer Science .– Springer Verlag, Heiderberg, Germany, 1978.–215 p.
Буч. Г. Объектно-ориентированный анализ.– М.: Бином, 1998. –560 с.
Jacobson I. Object-Oriented Software Engineering. A use Case Driven Approach, Revised Printing.– New York: Addison-Wesley Publ.Co, 1994.– 529 p.
Рамбо Дж, Джекобсон А., Буч Г. UML: специальный справочник.– СПб.: Питер, 2002.– 656с.
Лавришева Е.М., Грищенко В.Н. Связь разноязыковых модулей в ОС ЕС. – М.: Финансы и статистика.- 1982.- 136с.
Clements P., Northrop L. Software Product Lines: Practices and Patterns. SEI Series in Software Engineering, Addison-Wesley, 2001. ISBN-13: 978-0201703320.
Pohl K., Böckle G., van der Linden F. J. Software Product Line Engineering: Foundations, Principles and Techniques. Springer-Verlag, 2005. DOI: 10.1007/3-540-28901-1.
Bachmann F., Clements P. Variability in software product lines. CMU/SEI Technical Report CMU/SEI-2005-TR-012, 2005.
Classification of software engineering disciplines/ E. M. Lavrischeva.- Cybernetics and Systems Analysis, Vol. 44, No. 6, 2008
Лаврищева Е.М., Петренко Е.М. Моделирование семейства программных систем. - Труды ИСП РАН ю-Том 28, выпуск 6. – с49-65.
Ершов. А.П. Научные основы доказательного программирования.– Доклад АН СССР, 1985.–с.1–14.
Ершов А.П. Отношение методологии и технологии программирования, Конф. «Технология программирования» и ж. Программирование , 1986, № 3. 1986.–с.12–18.
Лаврищева Е.М., Грищенко В.Н. Сборочное программирование, 1991.-Наук.думка.- 213с.
Липаев В.В., Позин Б.А., Штрик А.А. Технология сборочного программирования, М., 1992.-324 с.
Лаврищева Е.М. Теория объектно-компонентного моделирования изменяемых программных систем.-www/ispras.ru/preprints/docs/prep_29_2015.pdf.
Лаврищева Е.М., Слабоспитская О.А. Технология моделирования изменяемых программных продуктов и систем//XII Межд. Научно-практ. конф. «Теоретические и прикладные аспекты построения программных систем».-TAAPSD’2015, 23-26 ноября, 2015.-с.118-128.
Глушков В.М. Теория автоматов и формальные преобразования микропрограмм // Кибернетика. – 1965. – № 5.– С. 1–10.
Капитонова Ю.В., Летичевский А.А. Методы и средства алгебраического программирования // Кибернетика. – 1993.–№ 3. – С. 7–12.
Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра. Языки. Программирование. - Киев, Наук.думка.-1974.- 287с.
Глушков В.М., В.Г.Бондарчук, Т.А.Гринченко и др. АНАЛИТИК-74, 79, 89, 93, 2000. – Кибернетика и системный анализ. –1995. –№5. –с.127–157.
Ющенко Е.Л. Адресный язык. - К.: Кибернетика на транспорте, 1962. - 52с.
Коваль В.Н. Концепторные языки. Доказательное проектирование. - К.: Наук.думка, 2001. - 182 с.
Коваль В.Н., Рабинович З.Л. Логико-алгебраический подход к верификации дискретных систем. - IV межд. Конференция Технология ПО-1995.
Глушков В.М. Основы безбумажной информатики –М.: Наука, 1982,- 281 С.
Глушков В.М. Кибернетика, ВТ, информатика (АСУ). – Избран. труды в 3-х томах. – К.: Наук. думка, 1990, 262 С, 267 С., 281 С.
Н.М.Задорожная, Е.М.Лаврищева. Управление документооборотом в ИС образования, Киев. - 2007. - Пед.Думка.-225 с.
Burstall R., Goguen I. The semantic of Clear, a specification language // Lect.Notes.Comp.Sci.-1980, v.86.-40p.
R. W. Floyd. Assigning meanings to programs, Proc. Symp. Appl. Math., 19; in: J.T.Schwartz (ed.), Mathematical Aspects of Computer Science, pp. 19-32, American Mathematical Society, Providence, R.I., 1967
Hoar К. О Структурной организации данных //Структурное программирование. – М.: Мир, 1975. – с.92 – 197.
Лаврищева Е.М. Software Engineering компьютерных систем. Парадигмы, технологии, CASE-средства программирования. - Наук.думка. -2014. - 284 с. –Изд. Юрайт, М.: 2015, 280 с.
Лаврищева Е.М. Программная инженерия. Теория программирования. –2016. - МФТИ.-51 с.
Лаврищева Е.М. Программная инженерия. Технология программирования. -2016 – МФТИ. - 52 с.
Лаврищева Е.М. Программная инженерия. Базовые основы ПИ. -2016 – МФТИ. - 52 с.
Лаврищева Е.М. Технология и инженерия моделирования изменяемых сложных систем. - 2017, Юрайт. - 432с.
Лаврищева Е.М. Карпов Л.Е., Томилин А.Н. Семантические ресурсы для разработки онтологии научной и инженерной предметных областей. - Труды конференции «Научный сервис в сети Интернет - 2016», 19-24 сентября 2016, Сборник трудов.- М.:ИПМ им. Келдыша, ISBN 978-5-98354-027-0. – c.223-239.
Островский А.И. Подход к обеспечению взаимодействия программных сред JAVA и MS.Net. - Проблемы программирования,- 2011.-№2.- с37-44.
MacGregor S.D., Sykes D.A. Practical Guide to testing Object-oriented Software. - 2001, Addison-Wesley Professional.
Об авторе: д.ф.-м.н.
Институт системного программирования им. В.П. Иванникова РАН, Москва
Материалы международной конференции Sorucom 2017
Помещена в музей с разрешения автора
14 сентября 2017
