А. А. Ляпунов и А. П. Ершов в теории схем программ и развитие ее логических концепций

[1]

Р. И. Подловченко

Цель этой статьи — обратиться к истокам и становлению теории схем программ, отметить фундаментальный вклад А. А. Ляпунова и А. П. Ершова в эту ветвь информатики и обсудить основные ее тенден-ции в настоящее время.

Данная статья написана в память об Андрее Ершове, оказавшем большое влияние на развитие теоретического программирования вообще и теории схем программ, в частности. Выбор именно этой теории не только отражает авторские пристрастия. Дело в том, что с нее начались систематические исследования теоретических вопросов программирования, и концепции, положенные в ее основу, были отправными в этих исследованиях. Раскрыть, в чем состоят логические концепции теории схем программ, — одна из задач данной статьи.

1.  Формирование научных предпочтений Андрея Ершова

Такое формирование относится к пятидесятым годам прошлого столетия, когда появились и стали развиваться электронные вычислительные машины. Возникла насущная необходимость в специалистах по их использованию.

Московский государственный университет в числе первых откликнулся на этот призыв времени. В 1950 году на его механико-математическом факультете была создана кафедра вычислительной математики, в задачи которой входило обучение студентов как методам численного анализа, так и применению их на вычислительных машинах. Вторая задача решалась впервые и по ходу создания самих машин, что потребовало поиска ее решения. В первые годы функционирования кафедры в программу обучения были включены предметы, нацеленные на изучение физической природы электронных вычислительных машин: годовые курсы электротехники и радиотехники, семестровый курс импульсной техники. Кроме того, студентам кафедры преподавались такие дисциплины, как теория механизмов и машин, теория аналоговых машин и черчение. Перечисленные предметы вытеснили математические дисциплины, такие как теория множеств, высшие разделы алгебры, функциональный анализ и математическая логика (заметим, что теория алгоритмов рассматривалась тогда только на специальных семинарах). Понятно, что с течением времени перекос в сторону дисциплин инженерного толка был устранен, и в программе обучения возобладал математический фундамент, однако недостаток его остро ощущался первыми выпускниками кафедры.

Андрей Ершов стал студентом кафедры вычислительной математики в 1951 году и «недополучил» в студенческие годы многие из необходимых ему в будущем математических знаний. Этот пробел, по счастью, был восполнен в его аспирантские годы, которые прошли под руководством Алексея Андреевича Ляпунова, позаботившегося о математическом образовании Андрея.

Вернемся к 1952 году, когда профессором кафедры вычислительной математики стал будущий отец российской кибернетики Алексей Андреевич Ляпунов. С его приходом научная жизнь кафедры сильно оживилась. Вера Алексея Андреевича в то, что электронным вычислительным машинам предстоит великое будущее, в сочетании с присущим ему энтузиазмом и даром убеждать повернули многих студентов кафедры лицом к программированию. В 1952/53 учебном году Алексей Андреевич прочел знаменитый курс лекций «Принципы программирования» (материал этого курса в несколько урезанной форме был издан только в 1958 году). Это был первый в стране курс лекций по программированию, и он сыграл фундаментальную роль в развитии как самого программирования, так и его теории.

Прежде всего, в этом лекционном курсе проявился новый взгляд на формализацию самого понятия «алгоритм», взгляд, исходящий из удобства использования формализованного алгоритма для решения практических задач. Новизна его в том, что существовавшие к тому времени формализмы: машины Тьюринга[2], нормальные алгоритмы Маркова[3] были нацелены исключительно на изучение природы вычислений, а не на практическое их использование.

В курсе, прочитанном Алексеем Андреевичем, был предложен операторный язык, явившийся предтечей алгоритмических языков программирования высокого уровня. С его введением стало возможным описывать приемы программирования. Операторный язык и приемы программирования на нем объединялись под названием операторного метода.

Эта благодать пролилась на Андрея Ершова, когда он был студентом четвертого курса.

Но пойдем дальше. Операторный язык не был формализованным, что не помешало, используя его, говорить о проблематике программирования. Таким образом, из ремесла программирование перешло в самостоятельную область науки со своим кругом задач.

Среди задач программирования Алексей Андреевич выдвинул на первый план две:

–    автоматизация построения программ;

–    оптимизация первоначально построенной программы.

Они рассматривались как взаимосвязанные, но каждая требовала самостоятельного решения.

К решению первой задачи Алексей Андреевич незамедлительно привлек студентов кафедры, и в их числе Андрея Ершова. Замысел ее решения был таков: алгоритм, подлежащий выполнению на вычислительной машине, записывается на операторном языке, и эта запись преобразуется в машинный код программы, выполняющей данный алгоритм. Воплощение этого замысла осуществляет так называемая программирующая программа, прообраз будущих трансляторов с алгоритмических языков программирования.

Программирующая программа конструировалась под руководством Алексея Андреевича, будучи разбита на блоки, выполняющие отдельные функции трансляции. Андрею Ершову было поручено построение арифметического блока. Эта работа стала первым шагом в исследованиях, проводимых Андреем в последующие годы и посвященных конструированию трансляторов. Результаты этих исследований отражены в [7]. Отметим, что уже при построении арифметического блока у Андрея Ершова зародилась идея экономии памяти, используемой оттранслированной программой, идея, которая переросла в общую задачу оптимизации программы в процессе ее трансляции.

2.  Ранние исследования в теоретическом программировании

Темы их были намечены Алексеем Андреевичем и восходят ко второй из выдвинутых им задач программирования.

Алексей Андреевич отталкивался от следующего положения: математическое решение проблемы оптимизации программы должно основываться на строгом определении самой программы, включающем описание ее структуры и функционирования. Только тогда можно говорить о функции, реализуемой программой, и ввести отношение функциональной эквивалентности программ требованием совпадения функций, ими реализуемых. Оптимизация программы должна выполняться посредством эквивалентных ее преобразований, т. е. преобразований, сохраняющих реализуемую программой функцию. И поэтому вслед за строгим определением программы должна рассматриваться задача построения эквивалентных преобразований (э. п.) программ.

Алексей Андреевич предполагал, что строгое определение программы может быть выполнено на основе операторного языка, и поставил эту задачу перед Андреем Ершовым, бывшим в ту пору его аспирантом. Интуиция подсказывала, что формализованная программа явится новым определением понятия «алгоритм», равноправным с уже существующими. Как факт, это было установлено Андреем Ершовым (см. [2, 3]). Введенное им понятие операторного алгоритма оказалось столь же универсальным, как и нормальные алгоритмы Маркова.

Вернемся к задаче построения э. п. программ. По математической традиции эта задача уточняется следующим образом: отыскать систему э. п., полную в данном классе программ. При этом полнота системы э. п. трактуется так: для любых двух эквивалентных программ из данного их класса существует конечная цепочка преобразований, принадлежащих системе, трансформирующая одну из пары программ в другую. Очевидно, что полная система является наилучшим решением задачи о построении системы э. п. программ для данного их класса.

Практический интерес представляет полная система, сопровождаемая алгоритмом, на вход которого подаются любые две программы из данного их класса и который в процессе построения цепочки преобразований устанавливает, эквивалентны эти программы или нет, трансформируя в первом случае одну программу в другую. Поиск такой полной системы возводится в ранг проблемы э. п. Необходимым условием ее положительного решения является разрешимость эквивалентности в данном классе программ, т. е. существование алгоритма, распознающего эквивалентность программ, принадлежащих этому классу.

Как уже было отмечено, интуитивно Алексей Андреевич ощущал, что программами можно описывать все вычислимые функции, откуда следует неразрешимость проблемы эквивалентности в достаточно богатом классе программ, следовательно, и неразрешимость проблемы э. п. в этом классе. Таким образом, надо нацелиться на построение неполных систем э. п. Аппарат необходимых для этого средств был заложен уже в операторном языке. Действительно, логическая схема, принадлежащая операторному языку, может использоваться двояко: как описание конкретного алгоритма и как описание класса алгоритмов, обладающих общей управляющей структурой. В первом случае на эту структуру нанизываются конкретные операторы и булевы выражения, а во втором случае — операторные символы и логические переменные, пробегающие множество операторов и соответственно множество булевых выражений, и каждому выбору значений тех и других отвечает свой алгоритм. Во втором случае логическая схема называется схемой программ.

Идея восприятия логической схемы как схемы программ состоит в следующем. Пусть в множестве схем программ введено «разумное» отношение эквивалентности, а именно: из эквивалентности схем программ всегда следует функциональная эквивалентность программ, представленных этими схемами (такая «разумная» эквивалентность называется аппроксимирующей функциональную эквивалентность программ). Тогда всякое эквивалентное преобразование схемы программ одновременно будет и эквивалентным преобразованием представленных ею программ. Это означает, что на схемах программ можно разрабатывать эквивалентные преобразования самих программ. Правда, полная система э. п. схем будет уже неполной системой э. п. программ, но зато можно рассчитывать на ее построение.

Исходя из изложенных соображений, Алексей Андреевич предложил своему аспиранту Юрию Ивановичу Янову следующую задачу: ввести отношения эквивалентности схем программ, которые хотя бы интуитивно были аппроксимирующими функциональную эквивалентность программ, и рассмотреть для каждой из введенных эквивалентностей проблему э. п. схем программ. Ю. И. Янов выполнил эту задачу (см. [27]), и проведенные им исследования стали первыми в научном направлении, получившем название теории схем программ, а исследованные схемы вошли в теорию под названием схем Янова. Заметим, что по справедливости они должны именоваться схемами Ляпунова—Янова.

Полученные Яновым результаты стали доступными для широкой программистской общественности с использованием графического представления схем программ, что было сделано Андреем Ершовым в [4]. Введенные Яновым эквивалентности схем программ действительно оказались «разумными», но это было установлено только с развитием соответствующего аппарата понятий (см. [14]).

Первые результаты в теории схем программ достойны строгого их изложения, это мы и сделаем, используя современный язык понятий.

Схемы программ строятся над некоторыми конечными алфавитами Y и P. Элементы Y и P называются соответственно операторными символами и логическими переменными (каждая переменная принимает значения из множества {0,1}).

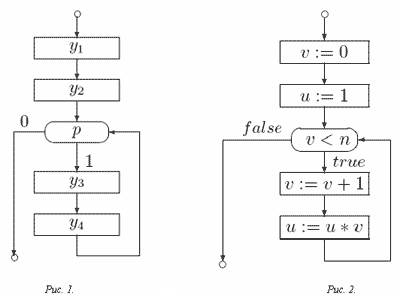
Схема программы (или просто схема) представляет собой конечный ориентированный граф с размеченными вершинами и дугами. Две вершины графа являются выделенными: вход — вершина без входящих в нее дуг и с одной исходящей и выход — вершина без исходящих из нее дуг; вход и выход не помечаются. Остальные вершины графа подразделяются на преобразователи и распознаватели. Каждый преобразователь имеет одну исходящую дугу, и ему сопоставлен символ из Y. Каждый распознаватель имеет две исходящие из него дуги, помеченные числами 0 и 1 соответственно, и ему сопоставлена переменная из P. Другие дуги графа не несут меток. Пример схемы программ, построенной над алфавитами дан на рис. 1. Эта схема построена по программе, вычисляющей n! для n ³ 0 и представленной на рис. 2.

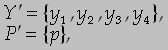
Функциональное описание схемы связано с процессом ее выполнения, который осуществляется на заданной функции разметки и состоит в путешествии по схеме, сопровождаемом накоплением цепочки операторных символов. При этом функция разметки определяется следующим образом.

Пусть

каждым элементом множества X фиксируются значения всех логических переменных из P. Функция разметки — это отображение множества 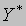, состоящего из всех слов над алфавитом Y, в множество X. Слова из 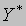называются операторными цепочками. Обозначим L множество всех функций разметки, построенных над алфавитами Y, P.

Перейдем к описанию функционирования схемы G, сконструированной над Y, P. Пусть m Î L. Выполнение схемы G на функции m начинается во входе схемы с пустой операторной цепочкой, прокладывает ориентированный путь в G и осуществляется по следующим правилам. Переход через преобразователь сопровождается приписыванием справа к текущей операторной цепочке символа, сопоставленного этому преобразователю; при этом путь в схеме продолжается по единственной исходящей из него дуге. Переход через распознаватель не меняет текущей операторной цепочки, а продолжение пути происходит по дуге, помеченной значением mh(p), где h — текущая операторная цепочка, а p — переменная, сопоставленная этому распознавателю. Процесс выполнения схемы G на m завершается только с достижением выхода схемы. Говорим, что в этом случае схема G остановилась на функции m, и результатом ее выполнения на m считаем накопившуюся к моменту остановки операторную цепочку.

В [27] Ю. И. Янов рассматривал параметрическое множество эквивалентностей схем над Y, P. Оно вводилось так. Распределением сдвигов в Y называлось отображение

Для выбранного s определялось множество  допустимых функций разметки:

Две схемы считались эквивалентными при выбранном s, если, какой бы ни была функция разметки из , всякий раз, как на ней останавливается одна из схем, останавливается и другая, причем с одинаковыми результатами.

Фундаментальный результат в [27] дается теоремой 1.

Теорема 1. Для любого распределения сдвигов s и индуцированного им отношения эквивалентности схем как проблема эквивалентности, так и проблема э. п. разрешимы в классе схем, каждая из которых использует не более одного раза любой символ из Y.

Разрешимость обеих проблем в множестве всех схем над Y, P была доказана позднее в [25].

3.  К характеристике первых результатов в теоретическом программировании

Вернемся к тому, что Андреем Ершовым в [2, 3] был установлен факт чрезвычайной важности: будучи формализованной, программа занимает равноправное положение среди других универсальных понятий алгоритма, т. е. программами реализуются все вычислимые функции. Но для множества вычислимых функций в [24] доказана неразрешимость проблемы эквивалентности, откуда вытекает неразрешимость для них и проблемы э. п. Таким образом, гипотеза Алексея Андреевича подтвердилась, и реальностью стали два альтернативных пути исследований: либо искать классы программ с разрешимой проблемой эквивалентности, либо довольствоваться построением неполных систем э. п. Моделирование программ схемами стало обоснованным.

В связи с этим приглядимся к результатам, полученным Ю. И. Яновым в [27]. Покажем, как характеризуются введенные там эквивалентности схем.

Введем два понятия: семантики базиса Y, P и индуцируемой ею абстрактной программы.

По определению, семантика базиса Y, P, обозначаемая как s, представляет собой комплекс, состоящий из

–    множества , элементы которого называются состояниями;

–    функций , yÎY;

–    отношений  

Процесс выполнения схемы G, построенной над Y, P, на паре , где , определяется следующим образом. Он состоит в путешествии по схеме G, прокладывающем в ней ориентированный путь и сопровождающемся преобразованием состояний из . Процесс начинается во входе схемы G при состоянии . Переход через преобразователь с символом y сопровождается преобразованием текущего состояния x в состояние sy(x). Переход через распознаватель не меняет текущего состояния x и состоит в выборе одной из исходящих из распознавателя дуг для продолжения путешествия по схеме; если p — сопоставленная распознавателю переменная, то выбирается дуга, помеченная значением sp(x). Выполнение схемы завершается, если путешествие по ней привело в выход схемы, и в этом случае текущее состояние воспринимается как результат выполнения G на паре. В ином случае результат не определен.

Схема G с присоединенной к ней семантикой s называется абстрактной программой. Последняя вычисляет функцию, которая отображает, в общем случае — частично, множество в себя. Две абстрактные программы, индуцированные семантикой s, эквивалентны тогда и только тогда, когда они вычисляют одну и ту же функцию.

Эквивалентность схем Янова, порожденная распределением сдвигов s, для которого

L_s = L,

называется строгой эквивалентностью. Тот факт, что она аппроксимирует эквивалентность абстрактных программ, устанавливается теоремой 2.

Теорема 2. Две схемы над базисом Y, P строго эквивалентны тогда и только тогда, когда соответствующие им абстрактные программы эквивалентны для любой семантики базиса Y, P.

Первоначально этот факт был установлен в [14].

Исследования, проводимые Ю. И. Яновым, шли параллельно и независимо с исследованиями в нарождающейся теории конечных автоматов. Связь между схемами Янова и конечными автоматами дается теоремой 3.

Теорема 3. Каким бы ни было распределение сдвигов в Y, индуцируемая им эквивалентность редуцируется к эквивалентности конечных автоматов.

Для строгой эквивалентности этот факт был установлен в [25], для других эквивалентностей, введенных Ю. И. Яновым, он следует из [21].

4.  О некоторых других задачах теории схем программ

Имеются в виду, прежде всего, рассмотренная А. П. Ершовым задача об экономии памяти и затем задачи, к которым он привлек внимание.

Схемы Янова абстрагируются от переменных, используемых реальной программой и составляющих используемую ею память. Задача ее экономии потребовала введения схем специального типа, отличных от схем Янова. Эти схемы отталкиваются от трактовки программы как объекта, ассоциируемого с потоком данных, когда каждое действие программы определяется переменными, воспринимаемыми как аргументы, и переменными, воспринимаемыми как результаты. Неформальное описание схем такого типа было предложено А. П. Ершовым в [1], формальное их определение дано позднее С. С. Лавровым в [9]. Вклад, сделанный А. П. Ершовым и С. С. Лавровым в решение задачи об экономии памяти программы, в деталях описан в [6], и это освобождает нас от описания его здесь.

А. П. Ершов индуцировал активные исследования схем программ, названных им стандартными схемами (см. [5]). В таких схемах используемые программой переменные представлены в явном виде, но в отличие от схем, рассмотренных С. С. Лавровым, для стандартных схем в качестве основных исследуются проблема эквивалентности и проблема э. п. Исследование стандартных схем наиболее полно описано в [8].

Особое внимание к стандартным схемам основано на следующем их свойстве: значительная часть полученных для них результатов переносится непосредственно на программы, для которых построены эти схемы. Чтобы убедиться в этом, обратимся к неформальному определению стандартной схемы.

Программы, моделируемые стандартными схемами, алголоподобны, но лишены описания переменных, ввода и вывода данных. Они конструируются над базисом, состоящим из операторов присваивания и булевых выражений, и используют все традиционные средства композиции операторов, кроме аппарата процедур. Пример такой программы дан на рис. 2.

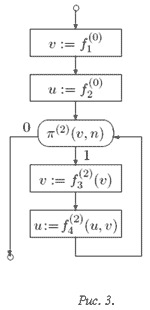
Переход от программы к стандартной схеме осуществляется заменой конкретных операций и отношений, используемых базисными операторами и булевыми выражениями, функциональными и предикатными символами соответственно; эти символы сохраняют арность замененных ими операций и отношений. Конструкции, полученные такой заменой из базисных операторов присваивания и булевых выражений, называются операторами над памятью и предикатами над памятью. Управляющая структура стандартной схемы берется совпадающей с управляющей структурой программы, индуцирующей схему. На рис. 3 приведена стандартная схема, построенная для программы, изображенной на рис. 2.

Опишем функционирование стандартной схемы.

Пусть I — интерпретация функциональных и предикатных символов, заменивших конкретные операции и отношения. Интерпретация I транслирует схему в I-программу. Реализуемая I-программой функция определяется теми же правилами, что определяют функцию, реализуемую исходной программой.

Две стандартные схемы считаются эквивалентными тогда и только тогда, когда при любой интерпретации I они превращаются в I-программы, реализующие общую для данной интерпретации функцию.

Заметим, что среди возможных интерпретаций имеется такая, которая транслирует схему в исходную программу. Поэтому эквивалентность стандартных схем всегда является аппроксимирующей функциональную эквивалентность программ, смоделированных этими схемами. Последнее означает, что результаты, полученные для стандартных схем и относящиеся к проблеме эквивалентности и проблеме э. п., применимы к реальным программам.

Описывая в [5] современное состояние теории схем программ,
А. П. Ершов сформулировал проблемы этой теории. Среди них важное место отведено проблеме эквивалентности.

Изучение стандартных схем началось с выявления таких их классов, для которых проблема эквивалентности неразрешима. Это было сделано в [10, 13]. Возникла задача отыскания классов схем с разрешимой проблемой эквивалентности. Подходы к исследованию этой задачи описаны в [5, 8]. Они базируются на установлении некоторых специальных ограничений, налагаемых либо на полугруппу базисных операторов, либо на структуру схем. Оба подхода вполне естественны. Но, в дополнение к ним, А. П. Ершов предложил некий новый подход. Его суть состоит в следующем.

Рассмотренная выше функциональная эквивалентность стандартных схем определяется требованием окончательных результатов их работы.
А. П. Ершов ввел понятие истории выполнения схемы и отношения эквивалентности схем по историям. Новый тип эквивалентности схем стал объектом дальнейших исследований, получивших особое признание в случаях, когда рассматриваемая эквивалентность по истории строже, чем функциональная (примером таковой является логико-термальная эквивалентность, обсуждаемая в [5]).

В [5] было показано, что эквивалентность по истории выполнения схемы, более строгая, чем функциональная, сводится к последней, рассматриваемой в некотором подклассе схем; он варьируется с выбором эквивалентности по истории. Для логико-термальной эквивалентности это сведение фактически выявлено в [26].

А. П. Ершов привлек внимание еще к одной задаче: он положил начало развитию специального подхода к конструированию полных систем э. п. схем. Дело в том, что в решении этого вопроса теория схем программ стартовала от устоев математической логики, оперирующей с формулами. В случае схем программ, представляющих собой размеченные графы, роль формулы стал играть фрагмент схемы, вообще говоря, отличный от схемы. Поэтому и возникла упомянутая выше задача. Пример нового подхода к конструированию полных систем э. п. продемонстрирован А. П. Ершовым в [4]. Позиция автора в этом вопросе будет изложена ниже.

5.  О логических основах теории схем программ

Они базируются на общей установке, сделанной А. А. Ляпуновым, а именно: схемы программ создаются для построения э. п. программ. Эта установка была поддержана Ю. И. Яновым и А. П. Ершовым в их работах, упомянутых выше. Будучи облечена в концепции, данная установка детализируется следующим образом.

Концепция 1. Исходной точкой конструирования схем программ является формализация понятия программы, т. е. строгое описание ее структуры и функционирования, на основе чего дается определение эквивалентности программ.

Концепция 2. Определение схемы программы, как и определение самой программы, слагается из описаний ее структуры и функционирования; вслед за этим вводится отношение эквивалентности схем программ. Эти построения должны подчиняться следующим условиям:

а)   управляющая структура схемы программы совпадает с управляющей структурой самой программы;

б)   эквивалентность схем влечет за собой эквивалентность программ, для которых построены схемы, т. е. первая аппроксимирует вторую.

Эти условия вытекают из назначения схем. Действительно, при выполнении условия а) преобразование схемы, затрагивающее ее управляющую структуру, является и преобразованием программы, порождающей эту схему; условие б) гарантирует, что всякое эквивалентное преобразование схемы будет и эквивалентным преобразованием программы, для которой построена схема.

Концепция 3. Ведущей проблемой для схем программ является проблема э. п.

Концепция 4. Моделирование программ схемами должно быть варьируемым, что достигается варьированием отношения эквивалентности схем программ. Действительно, так как решение проблемы э. п. схем дает неполную систему э. п. программ, то необходимо обеспечить выбор модели программ для получения более богатой такой системы.

Концепция 5. Фундаментальной в проблематике теории схем программ является проблема эквивалентности схем. Ее разрешимость в некотором классе схем является условием, подающим надежду на существование положительного решения проблемы э. п. в этом классе.

6.  Развитие логических концепций теории схем программ

В наиболее полном виде это развитие привело к ветви теории схем программ, названной алгебраической теорией моделей программ (короче: теорией моделей программ). Программы, рассматриваемые в этой теории как исходный материал, являются алголоподобными. Они классифицируются по признаку: используется или нет аппарат процедур (см. [16, 19]). Далее излагаются факты, относящиеся к случаю, когда программы не используют процедур [16—18].

В этом случае формализованные программы представляют собой введенные выше абстрактные программы, построенные над базисом Y, P. Семантика базиса Y, P предполагается произвольной.

Структура схемы программы берется совпадающей со структурой схемы Янова, представленной в графической форме. Следовательно, условие а) концепции 2 выполнено.

Следуя концепции 4, в множестве схем программ вводится параметрическое семейство эквивалентностей (см. [16]). Оно существенно расширяет множество эквивалентностей, рассмотренных Ю. И. Яновым в [27]. Всякая вводимая эквивалентность индуцируется двумя параметрами, а именно:

–    эквивалентностью n  в множестве;

–    подмножеством L, где LÍL.

(ν, L)-эквивалентность схем G₁,G₂, построенных над базисом Y, P, определяется требованием: какой бы ни была функция из L, всякий раз, как на ней останавливается одна из схем G₁,G₂,останавливается и другая, и результаты их выполнения — это n-эквивалентные операторные цепочки.

Множество всех схем над базисом Y, P, дополненное их (ν, L)-эквивалентностью, называется (ν, L)-моделью программ.

Следуя условию б) концепции 2, из множества (ν, L)-эквивалентностей отбираются строго аппроксимирующие. При этом (ν, L)-эквивалентность называется строго аппроксимирующей, если существует непустое множество S семантик базиса Y, P, такое, что для любых схем G₁,G₂, над базисом Y, P выполняется: G₁,G₂, (ν, L)-эквивалентны тогда и только тогда, когда для всякой семантики s из S эквивалентны абстрактные программы, индуцируемые этой семантикой из .

В [17] доказывается теорема 4.

Теорема 4. Если (ν, L)-эквивалентность схем над базисом Y, P является полугрупповой, то она — строго аппроксимирующая.

По определению, (ν, L)-эквивалентность — полугрупповая, если и только если удовлетворены следующие требования:

1)   для любых операторных цепочек h₁, h₂,h₃, h₄ из

2)   L состоит из n-согласованных функций разметки; при этом функция m из L называется ν-согласованной, если она удовлетворяет условию: для любых h₁, h₂, из

3)   множество L замкнуто относительно операции сдвига, т. е., какими бы ни были функция μ из L и цепочка h из , функция разметки μ', определяемая равенством

принадлежит множеству L.

Здесь запись  интерпретируется как запись отношения:h₁, h₂, — ν-эквивалентные операторные цепочки.

Заметим, что

–    эквивалентности схем, введенные Ю. И. Яновым, являются полугрупповыми;

–    эквивалентности дискретных преобразователей, обсуждаемые А. А. Летичевским в [11], будучи спроецированы на схемы программ, приводят к полугрупповым эквивалентностям схем.

Поскольку строгая аппроксимация — это частный случай просто аппроксимации, определенной выше, возникает вопрос: изучая полугрупповые эквивалентности, не теряем ли мы очевидно полезные эквивалентности схем программ. Ответ на него дается теоремой 5. Подготовим ее формулировку.

Пусть рассматриваются программы, являющиеся отправными при введении стандартных схем. Обозначим K их класс, предполагая, что они построены над некоторым конечным базисом операторов присваивания и булевых выражений. Согласно сделанному ранее описанию, при переходе от K к стандартным схемам, соответствующим программам из K, оператор присваивания заменяется оператором над памятью, булево выражение — предикатом над памятью. Обозначим K₁ полученный из K класс стандартных схем.

Предположим, что эквивалентность вK₁ строится, отталкиваясь от такой эквивалентности в K, которая требует совпадения результатов выполнения программы на каждой переменной, используемой программой. Далее. Если операторы присваивания заменить операторными символами, а булевы выражения — логическими переменными, то мы получим из программ класса K схемы Янова. Обозначим K₂  их класс. Пусть при этом между операторами над памятью (предикатами над памятью), используемыми вK₁, и операторными символами (логическими переменными), используемыми в K₂, имеется взаимно-однозначное соответствие. Оно индуцирует соответствие, тоже взаимно-однозначное, между схемами из K₁ и схемами из K₂.

Теорема 5. Можно так определить (ν, L)-эквивалентность в K₂, что схемы из K₁ будут эквивалентны тогда и только тогда, когда (ν, L)-эквивалентны соответствующие им схемы из K₂; при этом построенная (ν, L)-эквивалентность — полугрупповая.

Таким образом, очевидно полезная эквивалентность стандартных схем вписывается в множество полугрупповых эквивалентностей схем. Более того, последними эквивалентностями факторизуются первые.

Итак, нами показано, что теория моделей программ строилась согласно концепциям 1, 2 и 4. Концепции 3 и 5 отражены в ее проблематике. Раскроем преимущества создания семейства (ν, L)-моделей.

По определению, (ν₁, L₁) -эквивалентность аппроксимируется(ν₂, L₂) -эквивалентностью, если последняя влечет первую. Предположим, что это отношение имеет место, и пусть K — класс программ, эквивалентность которых аппроксимируется как (ν₁, L₁) -эквивалентностью, так и (ν₂, L₂)-эквивалентностью. Тогда при условии, что T_i  — это система э. п., полная в (ν_i, L_i)-модели, i = 1, 2, можно утверждать, что для класса K системаT₂ не беднее системы T₁ . Таким образом, располагая множеством моделей программ, можно обогащать систему э. п. программ, не покидая его.

Это обстоятельство приводит к задаче поиска условий, достаточных для аппроксимации одной эквивалентности другой эквивалентностью. Такая задача рассматривается в [23].

Обратимся теперь к проблеме эквивалентности схем. Обзор случаев ее разрешимости сделан В. А. Захаровым[4] на конференции  MCU 2001[5] и опубликован в [30]. Поэтому мы ограничимся описанием двух новых подходов к проблеме эквивалентности и обсудим наиболее важные из результатов, полученных их применением. Подчеркнем, что речь пойдет только о теории моделей программ.

Оба подхода нацелены на поиск алгоритмов, разрешающих эквивалентность схем программ за практически приемлемое время. Дело в том, что ранние исследования проблемы эквивалентности, проводимые в теории схем программ, были сфокусированы на установлении самого факта ее разрешимости; при этом игнорировалась сложность разрешающего алгоритма. Вполне приемлемой считалась процедура разрешения с экспоненциальной (относительно размеров испытуемых схем) временной сложностью. Легко согласиться с тем, что такие процедуры неприменимы на практике. Практически приемлемой можно считать процедуру, временная сложность которой полиномиальна. Это и послужило отправной позицией при разработке обоих подходов к проблеме эквивалентности.

Один из подходов состоит в поиске условий, достаточных для существования разрешающих эквивалентность алгоритмов полиномиальной сложности. Автором его является В. А. Захаров; найденные им достаточные условия опубликованы в [29]. Они даются формулируемой ниже теоремой 6. Введем используемые в ней понятия.

Начнем с того, что множество , в котором введена операция конкатенации цепочек, представляет собой конечно порожденную полугруппу. Ее элементы генерируются базовыми символами y, где yÎY; пустая цепочка является ее единицей.

Пусть ν — отношение эквивалентности в , и L — множествоν-согласованных функций разметки из L. Назовем (ν, L)-эквивалентность схем эквивалентностью относительно полугруппы  с отношением эквивалентности ν.

Полугруппа  с эквивалентностью n называется уравновешенной, если  удовлетворяет условию 1), изложенному в пояснениях к теореме 4, и, кроме того, если для любых h₁, h₂, из  из их ν-эквивалентности следует равенство их длин.

Зададимся уравновешенной полугруппой ; для любой цепочки h из  обозначим [h] класс эквивалентности цепочки h по отношению ν; длину цепочки h будем обозначать как |h|. Очевидно, что множество

 

является также конечно порожденной полугруппой.

Рассмотрим некоторую конечно порожденную полугруппу W с бинарной операцией ° и единицей e. Пусть в W выделена подполугруппа U и элементы ω⁺, ω^*, пусть κ₀ — натуральное число. Четверку K, где

    (1)

назовем κ₀ -критериальной системой для уравновешенной полугруппы , если выполнены следующие условия:

C1)   существует гомоморфизм j из E в U такой, что требование

выполнено для всех цепочек h, g из ;

C2)   для каждого элемента w из U⁰ω^* существует не более κ₀  левых обратных элементов из ω⁺U⁰ , т. е. уравнение

z° ω= e

имеет не более κ₀ различных решений z, представимых в виде

z=ω⁺°u

где u U.

Справедлива

Теорема 6. Пусть — уравновешенная полугруппа с отношением эквивалентности n, для которой имеется κ₀ - критериальная система (1), где κ₀> 0, и пусть в полугруппе W проблема тождества слов «верно ли, что ω₁=ω₂?» разрешима за время t(m), где

Тогда проблема эквивалентности схем относительно полугруппы  с отношением n разрешима за время

где n — максимум размеров двух схем, поступивших на вход разрешающего алгоритма, а константы c₁, c₂  зависят только от κ₀, числа элементов в Y и P и гомоморфизма j.

В [29], где доказана теорема 6, даны примеры конкретных уравновешенных полугрупп , к которым она применима. Одной из них является свободная коммутативная полугруппа, рассмотренная ранее в [20]. Эта полугруппа характеризуется следующими свойствами: в ней цепочки h₁, h₂, эквивалентны тогда и только тогда, когда любой символ из Y имеет равное число вхождений в одну и другую. Эквивалентность схем относительно свободной коммутативной полугруппы разрешима за время

где n определяется так же, как в теореме 6, а константа c зависит только от числа переменных в P.

Техника, используемая в [29], базируется на изучении алгебраических свойств полугрупп  с заданной в ней эквивалентностью цепочек.

Подход, альтернативный изложенному, предложен автором данной статьи; он описан в [22]. Этот подход базируется на вычислении инвариантов эквивалентных схем. Его применением в [22] получен следующий результат.

Теорема 7. Эквивалентность схем относительно полугруппы  с левым и правым сокращением разрешима за полиномиальное время.

Под полугруппой с левым и правым сокращением понимается уравновешенная полугруппа  с эквивалентностьюν,, которая разрешима и обладает свойствами:

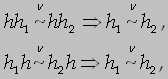
гдеh₁, h₂,h — произвольные цепочки из .

Заметим, что частным случаем такой полугруппы является свободная коммутативная.

Выполнив описание новых подходов к проблеме эквивалентности, обратимся к проблеме э. п. схем.

Конструирование систем э. п. схем следует традиции, присущей математической логике, а именно: создается формальное исчисление. Однако оно обладает чертами, не свойственными исчислениям, которые строятся в математической логике. Отметим их.

Объектами исчисления являются фрагменты схем (строгое определение фрагмента дается впервые в [28], затем уточняется в [21]); они составляют множество, содержащее все схемы, ибо схема — это частный случай фрагмента.

Единственным правилом вывода в таком исчислении является правило подстановки в схему вместо одного ее фрагмента другого. При этом заменяемый и заменяющий фрагменты должны быть согласованы так, чтобы результатом подстановки была опять-таки схема.

Операция подстановки сопоставляет всякой паре согласованных фрагментов множество преобразований схем. Согласованные фрагменты называются эквивалентными, если определяемое ими множество содержит только эквивалентные преобразования.

Аксиомами исчисления являются разрешимые множества, состоящие из пар эквивалентных фрагментов. Каждая аксиома индуцирует множество
э. п. схем, образуемое слиянием множеств, которые определяются входящими в аксиому парами фрагментов.

Система э. п. схем задается множеством аксиом, которые и индуцируют принадлежащие системе преобразования. Если при этом число аксиом конечно, то система э. п. называется конечной.

Таким образом, исчисление фрагментов схем берет на себя обязательства только по преобразованию схем, в ней строятся выводы схем из схем.

Отметим, что при выборе аксиом исключаются: случай, когда аксиома содержит все пары эквивалентных схем, и случай, когда аксиомой предписывается разметка фрагментов, а не изменение их структуры.

В [22], используя инварианты эквивалентных схем, мы доказали теорему 8.

Теорема 8. Для модели программ, построенной над базисом Y, P и такой, в которой эквивалентность схем индуцируется уравновешенной полугруппой  с левым и правым сокращением, существует полная в ней конечная система э. п. схем.

Этим результатом существенно обогащаются случаи разрешимости проблемы э. п. схем.

В заключение подчеркнем, что теория моделей программ действительно развивается в русле основных логических концепций, провозглашенных А. А. Ляпуновым и А. П. Ершовым на заре становления теории схем программ. При этом модели программ занимают естественное место в ряду других моделей вычислений, что подтверждается общностью рассматриваемых проблем и используемых при их решении методов.

Список литературы

1. Ershov  A. P. On programming of arithmetic operations// Communications of the ACM. — 1958. — Vol. 1, №  8. —  P. 3—6.
2. Ершов А. П. Операторные алгоритмы. 1. Основные понятия// Проблемы кибернетики. — 1960. — Вып. 3. — С. 5—48.
3. Ершов А. П. Операторные алгоритмы. 2. Описание основных конструкций программирования// Проблемы кибернетики. — 1962. —  Вып. 8. — С. 211—233.
4. Ершов А. П. Операторные алгоритмы. 3. Об операторных схемах Янова// Проблемы кибернетики. —  1968. — Вып. 20. — С. 181—200.
5. Ershov A. P. Theory of program schemata//  Proc. of IFIP Congress’71, Ljubljana. — 1971. — P. 93—124.
6. Ершов А. П. Введение в теоретическое программирование. — М.: Наука, 1977.
7. Ершов А. П. Избранные труды. — Новосибирск: Наука, Сиб. отд-ние, 1994.
8. Котов В. Е., Сабельфельд В. К. Теория схем программ. — М.: Наука, 1991.
9. Лавров С. С. Об экономии памяти в замкнутых операторных схемах// ЖВМ и МФ. — 1961. — Т. 1, № 4. — С. 687—701.
10. Летичевский А. А. Функциональная эквивалентность дискретных преобразователей// Кибернетика. — 1970. — № 2. — С. 14—28.
11. Летичевский А. А. Об эквивалентности автоматов над полугруппой// Теоретическая кибернетика. — 1970. — № 6. — С. 3—71.
12. Ляпунов А. А. О логических схемах программ// Проблемы кибернетики. — 1958. —   Вып. 1. — С. 46—74.
13. Paterson M. S. Program schemata// Machine Intelligence. — Edinburgh; Univ. Press, 1968. — Vol. 3. —  P. 19—31.
14. Подловченко Р. И., Петросян Г. Н., Хачатрян В. Е. Интерпретация схем алгоритмов и различные типы отношений эквивалентности между схемами// Известия АН Арм. ССР. Сер.  Математика. — 1972. — Т. 7, № 2. — С. 140—151.
15. Подловченко Р. И. О корректности и содержательности некоторых отношений эквивалентности между схемами Янова//  Проблемы кибернетики. — 1978. — Вып. 33.
16. Подловченко Р. И. Иерархия моделей программ// Программирование. — 1981. — № 2. — С. 3—14.
17. Подловченко Р. И. Полугрупповые модели программ// Программирование. — 1981. — № 4. — С. 3—13.
18. Подловченко Р. И. Модели программ над структурированным базисом// Программирование. — 1982. — № 1. — С. 9—19.
19. Подловченко Р. И. Рекурсивные программы и иерархия их моделей// Программирование. — 1991. — № 6.
20. Подловченко Р. И., Захаров В. А. Полиномиальный по сложности алгоритм, разрешающий коммутативную эквивалентность схем программ// Докл. РАН. — 1998. — Т. 362, № 6. — С. 744—747.
21. Подловченко Р. И. От схем Янова к теории моделей программ// Математические вопросы кибернетики. — 1998. — Вып. 7. — С. 281–302.
22. Подловченко Р. И. Об одном массовом решении проблемы эквивалентных преобразований схем программ// Программирование. — 2000. — № 1.— С. 66—77; № 2. — С. 3—11.
23. Подловченко Р. И., Попов С. В. Аппроксимируемость одних моделей программ другими// Вестник МГУ. Сер. Вычислительная математика и кибернетика. — 2001. — № 2. — С. 38—46.
24. Rice H. G. Classes of recursively enumerable sets and their decision problems// Transactions of American Mathematical Society. — 1953. — Vol. 89. — P. 25—59.
25. Rutledge J. D. On Ianov’s program schemata// J. of the ACM. — 1964. — Vol. 11. — P. 1—9.
26. Sabelfeld V. K. An algorithm for deciding functional equivalence in a new class of program schemata// Theoret. Comput. Sci. — 1990. — Vol. 71. — P. 265—279.
27. Янов Ю. И. О логических схемах алгоритмов// Проблемы кибернетики. —  1958. — Вып. 1. — С. 75—127.
28. Янов Ю. И. О локальных преобразованиях схем алгоритмов// Проблемы кибернетики. — 1968. — Вып. 20. — С. 201—216.
29. Захаров В. А. Быстрые алгоритмы разрешения эквивалентности операторных программ на уравновешенных шкалах// Математические вопросы кибернетики. — 1998. — Вып. 7. —  С. 303—324.
30. Zakharov V. A. The equivalence problem for computational models: decidable and undecidable cases// Lect. Notes Comput. Sci. — 2001. — Vol. 2055. —  P. 133—153.

Примечание

[1] © Р. И. Подловчено, 2004. Статья написана специально для настоящего сборника.

[2] Алан Матисон Тьюринг (1912—1954) — английский математик, логик, криптограф, изобретатель Машины Тьюринга — математической абстракции, представляющей вычислительную машину общего вида.

[3] Андрей Андреевич Марков (1903—1979) —  математик и логик. Профессор ЛГУ с 1935 г. С 1959 г. заведующий кафедрой математической логики МГУ. Член-корреспондент АН СССР (1953). Труды по топологии, математической логике и конструктивной математике.

[4] Владимир Анатольевич Захаров (р. 1960) — доцент кафедры математической кибернетики МГУ.

[5] MCU 2001 — Третья международная конференция «Машины, вычисления и универсальность», Кишинев, Молдова, май 2001 г.

 

Из сборника «Андрей Петрович Ершов — ученый и человек». Новосибирск, 2006 г.
Перепечатываются с разрешения редакции.