Первая отечественная многопроцессорная ЭВМ М-10
Гливенко Е.В., Прядко С.А., Фомочкина А.С.
В 70-х годах прошлого столетия в Советском Союзе была создана многопроцессорная машина М-10. Система М-10 первоначально была ориентирована на обработку больших потоков информации с помощью алгоритмов, обладающих более или менее естественным параллелизмом. Кроме того, предполагалось, что обработка должна производиться в реальном масштабе времени.
Архитектура машины М-10 принципиально отличалась от архитектур других многопроцессорных машин. Это была система, организованная на синхронном принципе, которая в каждом такте выполняла одновременно действия трех операторов: управляющего оператора, вычислительного оператора, преобразовывающего функции, и оператора, выполняющего геометрические преобразования. Обладая общей памятью, машина М-10 осуществляла общение с этой памятью целиком функциями, заданными в большом числе точек.
Архитектура машины М-10 была нетрадиционной. Прежде всего, принцип ее работы не предполагал, что распараллеливаемая на ней программа изначально будет написана на каком-либо языке и иметь последовательную структуру. Идея построения машины была взята из области математики, а именно из функционального анализа, где изначальным элементом является не число, как в математическом анализе, а функция целиком. Отсюда и возникло название «функциональная арифметика». Действия с функциями названы операторами. В машине М-10 нет числовой части. На вход машины поступают не числа, а функции, заданные в конечном числе точек. Система операторов машины – это не набор арифметических действий, а набор преобразований функций в функции. Многопроцессорность определяется числом точек, в которых задается функция. Пользователю предлагается довольно обширный инструментарий для работы над функциями, заданными таким образом. Пользователю предлагается самому «распараллелить» свою задачу, представив ее в виде набора функций на входе и в виде предполагаемых результатов – также функций – на выходе. Эта машина больше всего напоминает векторную или матричную машину, но, естественно, с более обширным набором операций. Проблемой при создании такой архитектуры явилось требование, чтобы набор операторов этой машины был полным. Это значит, что любой мыслимый оператор над функциями, задаваемыми в конечном числе точек, должен иметь возможность быть представленным в виде «программы», составленной из операторов машины. Набор операторов М-10 удовлетворяет условиям полноты [1, 2], а при выборе системы операторов учитывались также требования удобства «программирования».
Выбранная архитектура машины М-10 позволила эффективно использовать ее в виде управляющей машины на различных объектах. Это удавалось, главным образом, за счет возможности перенесения в «железо» большинства функций операционных систем, а также устройств сопряжения. Эта машина хорошо зарекомендовала себя при обработке локационной информации [3] при наблюдении за спутниками, при обработке снимков с пузырьковых камер [4] ускорителя, а также в задачах численного моделирования в физике и геофизике.
Основы архитектуры. Функциональной арифметикой будем называть многопроцессорную структуру, состоящую из большого числа отдельных процессоров, работа которых синхронизирована специальным образом.
В состав функциональной арифметики входят следующие компоненты: многоразрядная и одноразрядная структуры, память и устройство управления. Все структуры, как многоразрядные, так и одноразрядные, состоят из одинакового числа процессоров, причем каждый процессор многоразрядной структуры связан со своим одноразрядным процессором. Число процессоров в каждой структуре nl, где l определяет размерность функциональной арифметики, а n определяет наполнение каждого из направлений. Отдельный процессор многоразрядной арифметики имеет дело с m-разрядными числами, в соответствии с этим в его составе имеются m-разрядные регистры для записи операндов и результатов. Одноразрядный процессор имеет одноразрядные регистры.
Многоразрядная структура служит для работы с функциями f(x1, …,xl) l переменных, заданных соответственно в n точках по каждому из l направлений, т.е. всего в nlточках. Входные и выходные регистры отдельных процессоров объединяются во входные и выходные регистры всей структуры, и записанная в них информация интерпретируется как значения некоторой функции f(x1, …,xl), заданной в nl точках. Каждой точке при этом соответствует свой процессор. В каждой точке функция задается с помощью m-разрядного числа.
Отдельные устройства функциональной арифметики синхронизированы, и работа всей системы может быть представлена в виде последовательности операторов. Операторы функциональной арифметики ставят в соответствие паре функций, заданных во входных регистрах структуры, функцию-результат, которая располагается в выходных регистрах. Операторы функциональной арифметики можно разделить на три типа: операторы многоразрядной структуры, операторы одноразрядной структуры и операторы в которых участвуют обе структуры.
На вход операторов первого типа поступают функции из входных регистров многоразрядной структуры, и в виде результатов также получаются функции многоразрядной структуры. Операторы второго типа имеют дело с функциями, записанными в регистрах одноразрядной структуры. Такие функции принимают всего два значения (нуль и единица) и служат для выделения какого-либо множества. По аналогии с соответствующим термином из математики будем называть их характеристическими функциями множеств. Фактически операторы одноразрядной структуры осуществляют операции над множествами. В операторах третьего типа задействованы как функции, так и множества, как в виде операндов, так и в виде результатов. Операторы третьего типа служат для того, чтобы преобразовывать функцию на некотором множестве или получать в виде результата некоторое множество, связанное с функцией.
Далее рассмотрим конкретные типы функциональной арифметики. При l=2 такую арифметику будем называть функциональной плоскостью, при l=1 – функциональной линейкой. Функции, используемых в линейках, будем называть логическими, так как области их определения дискретны. По аналогии с этим операторы функциональной арифметики будем называть логическими. Для того чтобы можно было любой логический оператор реализовать на функциональной арифметике в виде программы, т.е. в виде последовательности операторовкоманд, необходимо, чтобы операторы-команды составляли полную систему.
Функциональная плоскость. Покажем идею построения архитектуры, называемой функциональной плоскостью, на абстрактном математическом примере.
Рассмотрим конкретную задачу (задачу Дирихле): найти решение уравнения Лапласа:
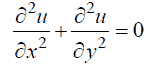 (1)
(1)
внутри некоторой двумерной области G. Причем решение на границе области должно совпадать с некоторой заданной функцией f , т.е. принимать некоторые конкретные значения.
Известен стандартный итерационный метод приближенного решения этой задачи, заключающийся в следующем. Разобьем координатную плоскость (x, y) на квадраты со стороной h прямыми, параллельными осями координат, и выберем систему квадратов таким образом, чтобы вся область была покрыта этой системой квадратов. Приближенное решение задачи Дирихле будем искать в узлах полученной сетки. Перенумеруем все внутренние узлы. Пусть их число будет N. Для каждого внутреннего узла запишем равенство, составляющее смысл приближенной конечноразностной схемы:
![]() (2)
(2)
Аргументом для логического оператора будем считать логическую функцию f ( x , y) двух переменных, определенную в узлах сетки. Полагаем, что она задана в некотором многоугольнике, содержащем область G.
Введем следующие операторы:
A сдвига по x вправо – оператор одновходовый, который функции f(x,y) ставит в соответствие функцию
A(f(x,y))=f(x-h, y);
A сдвига по x влево A(f(x,y))=f(x+h, y);
A сдвига по y вверх A(f(х,y))=f(x, y-h);
A сдвига по y вниз A(f(x,y))=f(x, y+h);
AΣ оператор суммирования – двухвходовый оператор
AΣ (f1 (x,y), f2 (x,y))= f1 (x,y)+ f2 (x,y);
A* – оператор умножения двух функций
A* (f1 (x,y), f2 (x,y))= f1 (x,y) × f2 (x,y).
Предполагается возможность маскирования операторов, т.е. выполнение оператора только на некотором подмножестве области определения функций, входящих в оператор.
Предположим, что архитектура ЭВМ такова, что можно:
- хранить целиком логические функции в виде таблиц в регистре, который представляет собой сетку, аналогичную плоскости;
- выполнять оператор над одной функцией, заданной в регистре, так, чтобы результат оказался в другом аналогичном регистре, не изменив содержимого первого;
- выполнять оператор над парой функций, находящихся в двух регистрах, так, чтобы результат оказался в третьем регистре.
Для маскирования операторов введем еще один регистр, так называемый «ковер». Он такой же многоугольный, с таким же расположением узлов, как регистр для хранения функций. Разница лишь в том, что в каждом узле ковра хранится всего 1 бит информации, тогда как в каждом узле регистра, хранящего функцию, число разрядов, определяется точностью задания функции. Можно считать, что на ковре располагается характеристическая функция некоторого множества, а именно того множества, в точках которого функция равна единице.
Например, с помощью ковра можно выделить область для описанной выше задачи как вместе с границей, так и без нее, т.е. множество ее внутренних точек.
Рассмотрим программу, состоящую из последовательности представленных операторов и реализующую решение задачи. Дирихле.
Прочтем из памяти в регистр следующую информацию: в точках границы области заданные краевые значения, а во внутренних точках области значения, равные нулю, которые представляют нулевое приближение решения задачи Дирихле. Обозначим эту функцию u0(x,y), сформируем первое приближение u1(x,y) по формуле (2). Для этого ко всем точкам применим оператор сдвига вправо по x на одну позицию. Запомним результат в отдельном регистре A. Затем сделаем сдвиг u0 по x влево на одну позицию. Запомним результат в другом регистре B. Сложим содержимое регистров A и B под маской, маской же выделим при этом только множество внутренних точек области. Результат запомним в регистре C.
Следующей командой выполним оператор сдвига исходной функции u0(x,y) вверх на одну позицию, результат запомним в регистре B. Затем сдвинем исходную функцию u0 вниз на одну позицию, а результат запомним в регистре B. Сложим содержимое регистров A и B под маской, выделяющей внутренние точки области. Содержимое отправим в регистр D.
Следующая операция сложит содержимое регистров С и D опять только во внутренних точках области с записью результата, например в регистре C. После этого опять только на внутренних точках области произведем умножение содержимого регистра C на функцию-константу, равную во всех точках числу 1/4.
После этих операций во всех внутренних точках области одновременно окажется приближение u1(x,y). При маскировании будем предполагать, что вне внутренних точек сохранятся предыдущие значения, т.е. краевые условия. Следующие приближения получим по той же программе.
Функциональная линейка. Приведенная многопроцессорная структурная плоскость удобна для решения двумерных задач. Для решения трехмерных задач удобнее была бы структура, построенная аналогичным образом, но имеющая три измерения. Однако же и в одномерном случае такая структура позволяет широко использовать параллелизм для решения широкого круга задач. Структуру, аналогичную функциональной плоскости, но имеющую одно измерение, будем называть функциональной линейкой.
Такая структура работает с логическими функциями от одного переменного. Функциональная линейка – это арифметическое устройство, которое в каждом такте выполняет преобразование над одной или несколькими логическими функциями. В каждом такте выполняется один логический оператор. В частности этот оператор может быть функционалом, т.е. в результате его действия получится не функция, а число. Естественно, возможности функциональной линейки меньше, чем у функциональной плоскости. Тем не менее, используя несколько функциональных линеек различных видов в одной структуре, можно организовать их взаимодействие так, чтобы обеспечивалось хорошее распараллеливание задач.
Пусть арифметическое устройство, реализующее функциональную линейку, снабжено четырьмя регистрами A, B, C, D. Каждый из этих регистров хранит информацию о логической функции. В соответствии со структурой логической функции регистр поделен на n частей (n-число точек, в которых задается функция). Каждая часть содержит m разрядов. Таким образом, каждый регистр A, B, C, D содержит по n×m разрядов. Будем считать, что значение аргумента для функции задается позиционно, значения аргумента нумеруются слева от 0 до n-1. В реальных задачах имеют дело с функцией, заданной в конечном числе точек x1,…, xn. Тогда в регистре будут записаны последовательно значения функции в точках x1,…, xn.
Регистры A и C считаем входными для арифметического устройства. Регистры B и D – выходные, в них помещается результат, получаемый после применения логического оператора.
Для полноразрядного арифметического устройства, т.е. для устройства, где m велико, удобна следующая система операторов, служащая системой команд:
| Поточечный оператор: | Двум функциям, расположенным в регистрах A и C, ставятся в соответствие: |
| 1. A+C | их сумма в соответствующих точках |
| 2. A – C | разность |
| 3. ¦A¦+¦C¦ | сумма модулей |
| 4. ¦A¦–¦C¦ | разность модулей |
| 5. A×C | произведение |
| 6. A : C | частное |
| 7. ¦A+C¦ | модуль суммы |
| 8. ¦A–C¦ | модуль разности |
| 9. MAKC | функция, равная максимальному из значений первой и второй функций в соответствующих точках |
| 10. MИН | функция, равная минимальному из значений первой и второй функций |
| 11. ¦MAKC¦ | функция равная модулю максимального значения первой и второй функций |
| 12. ¦МИН¦ | функция равная модулю минимального значения первой и второй функций |
13. СДВИГ – оператор, носящий название «сдвиг логический». Оператор одновходовый. Функции f, расположенной в регистре A, ставится в соответствие функция ? , такая, что ?(xi)=f (xi-1), i =2, …, n и ?(xi)=0. Этот оператор имеет модификации. Модификация, называемая «кольцевым сдвигом», отвечает формуле ?(xi)=f(xi-1) для i =2, …, n. ?(xi)=f(xn). Модификациями являются операторы, называемые «сдвигами влево». Им соответствуют формулы ?(xi)= f(xi+1), i=1, …, n-1, и ?(xn)=0 для не кольцевого сдвига, ?(xi)= f(xi+1), i=1, …, n-1, и ?(xn)= f(x1) для кольцевого сдвига;
14. СДВАЛГ – оператор, носящий название «сдвиг алгебраический». Это также одновходовый оператор, построенный аналогично сдвигу логическому с одной лишь разницей: при алгебраическом сдвиге сдвигаются только абсолютные значения функции, значения знаковых разрядов результата совпадают со значениями знаковых разрядов аргумента в соответствующих точках;
15. ¬A – оператор – отрицание. В каждом разряде регистра-результата появляется информация, противоположная той, которая содержится в соответствующем разряде регистра A;
16. A∨C – логическая сумма;
17. A∧C – логическое произведение.
18. ¬A∨C – логическая сумма отрицания значения соответствующего разряда регистра A и значения разряда регистра C;
19. ¬A∧C – логическое произведение отрицания значения соответствующего разряда регистра A и значения разряда регистра C.
Далее приведем операторы, являющиеся функционалами. На вход такого оператора поступают функции, на выходе получается число. Из описания этих операторов будет видно, что это число должно задаваться большим числом разрядов, чем входные функции. При применении оператора в регистр результата B или D, содержащий mxn разрядов, принимается число – результат, как в единый длинный регистр.
20. ∑AC – оператор – «скалярное произведение». Число, получающееся в результате применения этого оператора, равно сумме попарных произведений значений входных функций из A и C по всем точкам;
21. ∑A – сумма по всем точкам значений входной функции из регистра A;
22. ∑A|C| – оператор, аналогичный «скалярному произведению». Разница заключается в том, что берутся парные произведения значения функции из регистра A и модуля значения функции из регистра C;
23. B+∑AC – число, получаемое после применения этого оператора и равное сумме двух чисел: числа, содержащегося к этому моменту в регистре B (многоразрядного), и суммы парных произведений значений функций из A и из C по всем точкам.
24. B+∑A – число, получаемое после применения этого оператора и равное сумме двух чисел: числа (многоразрядного), содержащегося к этому моменту в регистре, и суммы значений функции, содержащейся в регистре A, по всем точкам;
25. B+∑A|C| – число, получаемое после применения этого оператора и равное сумме двух чисел: числа, содержащегося к этому моменту в регистре B (многоразрядного), и суммы попарных произведений значений функции в соответствующих точках из регистра A на модуль значений функции из регистра C.
Следующие операторы относятся к случаю, когда m=1 (регистры Ri содержат по n разрядов);
26. Ri ∨Rj=Rk – содержимое i-го регистра поразрядно складывается с содержимым j-го регистра и результат отсылается в k-й регистр. Индексы i, j, k могут принимать любые значения 1,…3; в частности, все индексы или какие-либо из них могут быть равными;
27. Ri∧Rj=Rk – оператор выполняется аналогично предыдущему с той разницей, что вместо логического суммирования производится логическое умножение;
28. Ri+Rj=Rk – оператор производит сложение содержимого регистров Ri, Rj как чисел с фиксированной точкой;
29. Ri –Rj=Rk – оператор производит;
30. ∨Ri – оператор интегральной дизъюнкции;
31. ∧Ri – оператор интегральной конъюнкции;
При применении этих операторов получается одноразрядное число, равное либо нулю, либо единице. При применении оператора 30 результат равен единице, если есть единица хотя бы в одном разряде регистра Ri. В противном случае результат равен нулю;
32. Левая граница – в регистре Rk появляется единственная единица в самом левом разряде из тех, где были единицы в Ri;
33. Правая граница;
34. j – размножение – во всех разрядах Rk устанавливаются значения, совпадающие со значением j – го раз
ряда регистра Ri
Следующие операторы будут распространяться на линейке обоих типов одновременно:
35. Индикация левого максимума – оператор работает с регистрами A и Ri. У функции, расположенной в регистре A, ищется максимальное значение, которое появляется в виде функции-константы в регистре результата. Одновременно с этим в том разряде регистра Ri, который соответствует самой левой точке из тех, в которых достигается максимальное значение, появляется единственная единица;
36. Индикация правого максимума – оператор аналогичен предыдущему с той лишь разницей, что в Ri появляется единица, соответствующая самому правому максимуму;
37. Размножение левого максимума по модулю – оператор, в котором процедура повторяет предыдущие операторы, но максимум берется по модулю;
38. Размножение правого максимума по модулю;
39, 40, 41, 42 – операторы повторяют операторы 35, 36, 37, 38 с заменой слова «максимум» на слово «минимум»;
43. Оператор «перестановка» – оператор берет функцию из регистра A, меняет в ней местами точки (по круговому циклу), «обозначенные» регистрами Ri (т.е. к этому моменту в регистре Ri в соответствующих разрядах стоят единицы), и полученную функцию отправляет в регистр результата;
44. Оператор «высечение уровней» – оператор в тех разрядах регистра Ri, которые соответствуют точкам регистра A, где f(x)=y0, устанавливает единицы, в остальных разрядах – нули.
Представим некоторые функционалы, реализуемые с помощью линеек обоих типов;
45. MAX|A–C| – нахождение числа, равного максимуму по всем точкам модуля разности функций A и C. В Ri появляются единицы в тех разрядах, где значение модуля разности максимально;
46. ∑|A – C| – нахождение числа, равного сумме по всем точкам квадратов разностей двух функций. При этом в Ri появляются единицы в тех разрядах, где квадраты разностей минимальны.
Организация работы функциональной арифметики. В предыдущем пункте были описаны основные операторы функциональных линеек для двух случаев. В первом случае предусматривается работа с многоразрядными числами, выступающими в виде значений функций, во втором случае значения функции полагались равными либо нулю, либо единице.
Оба вида функциональных линеек должны присутствовать в устройстве «функциональная арифметика», и каждой из них в устройстве отводится самостоятельная роль.
Предположим, что нужно реализовать некоторую вычислительную процедуру, имеющую целью решение конкретной математической задачи. Пусть входными величинами этой процедуры будут функции от одного действительного переменного, заданные в конечном числе точек, естественно, с конечным числом разрядов, Предполагается получить результат в виде набора функций.
Попробуем, если это возможно, а опыт показывает, что в большинстве случаев это так, записать предполагаемую вычислительную процедуру в виде параллельного алгоритма, ориентированного на данную структуру. В отличие от обычного алгоритма, представляющего собой набор вычислительных тактов, в каждом из которых производится одна из вычислительных операций (сложение, вычитание, умножение и деление с парой операторов, числами), в данном случае, алгоритм будет представлять собой последовательность тактов, в каждом из которых реализуется один из работающих операторов функциональной линейки с парой операндов, логическими функциями.
Установим, что считать работающими операторами функциональной линейки. Это будут операторы, описанные в пункте Функциональная линейка для многоразрядной линейки, взятые «под маской». Маскирующими множествами могут быть любые подмножества множества точек, в которых задана функция. Эти подмножества задаются с помощью характеристических функций, расположенных в регистрах второй функциональной линейки, которая работает с двузначными функциями.
Эти признаки следующие:
W – признак переполнения результатов разрядной сетки;
z – признак равенства результата нулю;
E – признак равенства операндов или их модулей, если операция выполняется над модулями;
M – признак выполнения неравенства C>A или ¦C¦>¦A¦, если операция выполняется над модулями;
s – признак отрицательного результата.
Итак, в одном такте одного оператора основной функциональной линейки вырабатывается шесть одноразрядных признаков.
После каждого такта работы основной функциональной линейки любые из пяти строк признаков могут быть запомнены в регистрах Ri, которые являются регистрами одноразрядной функциональной линейки и которые иначе называются регистрами признаков. Запомненная в некотором такте информация о признаках может служить маскирующей характеристической функцией для выполнения в следующем такте некоторого оператора уже под маской.
Электронная вычислительная машина М-10 как вариант функциональной арифметики. Электронная вычислительная машина М-10 – это вариант функциональной арифметики. М-10 [5] – синхронная многопроцессорная ЭВМ: в ее состав входит ряд процессоров различного типа, которые могут работать параллельно (синхронно), т.е. в течение одного машинного такта процессора. Для реализации такого способа функционирования в программе машинная команда М-10 содержит список операций для процессоров, которые должны быть инициированы в данном такте. Практически все операции управления и арифметики выполняются за один машинный такт.
В состав М-10 входят процессоры следующих типов. Первый тип – арифметические процессоры, которые физически реализованы в виде двух независимых арифметических устройств, синхронно выполняющих разные арифметические или логические операции. Каждое устройство представлено в виде одного, двух, четырех или восьми процессоров в зависимости от разрядности входных операндов, заданной в арифметической операции. С точки зрения программиста в одной команде максимально может быть задействовано два процессора по 128 разрядов: 4x64, 8?32 или 16x16, причем каждый процессор может производить двухместную операцию над операндами указанной разрядности. В этом смысле можно говорить о том, что в М-10 реализованы две независимые функциональные линейки. Каждая линейка может иметь различное число точек, что связано с точностью представления чисел. Если потребуется точность, соответствующая 128-разрядной сетке, то в каждой линейке будет присутствовать всего одна точка. При 64-разрядной сетке в каждой функциональной линейке будут по две точки, в случае 32 разрядов – по четыре точки и в случае 16 разрядов – по восемь. В каждой функциональной линейке есть четыре оперативных регистра: входные A и C и выходные B и D. Эти регистры содержат по 128 разрядов. Максимальное число точек, на которое разбиваются эти регистры, – восемь.
Каждая линейка может выполнить в одном такте один из следующих операторов: A + C; A – C; A × C; A : C; A+, C; A–, C; A + C ; A − C ; СДВИГ; СДВАЛГ; ¬A; A ∨C; A ∧C; A ∧C; ¬A ∨C; ¬A ∧C.
Из функционалов имеются следующие: Σ A×C , Σ A, Σ A. C .
Ко второму типу процессоров, работающих синхронно с арифметическими, относится устройство управления. Устройство управления реализует одну функциональную линейку длиной в 16 точек, в каждой точке функция может принимать только два значения – 0 или 1. Набор операторов этой линейки следующий: поточечное логическое умножение. Из функционалов следует отметить: интегральную дизъюнкцию; интегральную конъюнкцию. Линейка устройства управления реализована с помощью трех 16-разрядных регистров R1, R2, R3. Каждый из них может служить регистром, как для операнда, так и для результата. Для результатовфункционалов предусмотрены два одноразрядных регистра – триггера T1 и T2. В устройстве управления реализованы дополнительно:
– полноразрядная арифметика с фиксированной точкой на регистрах R1, R2, R3;
– условные переходы по содержимому триггеров T1 или T2.
Регистры R1, R2, R3 называются регистрами признаков. Это связано с тем, что согласно идее организации функциональной арифметики в регистры R1, R2, R3 могут быть приняты признаки, вырабатываемые в арифметических линейках, и, наоборот, содержимое регистров R1, R2, R3 может восприниматься в виде маски для выполнения операторов под маской.
Устройство управления наряду с манипуляциями с регистрами признаков и одновременно с ними, а также, естественно, параллельно с основной арифметикой может выполнять еще полный набор операций с фиксированной точкой с содержимым регистров адресных модификаторов. Таких модификаторов в М-10 шестнадцать. Каждый из них содержит 22 разряда, что соответствует разрядности адреса памяти М-10.
Третий тип процессоров М-10 составляют два синхронно работающих канала связи процессор – память, предназначенных для чтения операндов из памяти во входные регистры арифметических процессоров и записи результатов операций. Максимальная ширина доступа в память по одному каналу составляет 512 бит, что позволяет заполнять входные регистры всех арифметических процессоров за одно обращение. Обращение к памяти осуществляется по виртуальному адресу в формате «индекс, база, смещение». Разрядность смещения разряда, минимальный адресуемый элемент памяти – полуслово (16 бит). Общая емкость внутренней памяти 5 Мбайт/с.
Четвертый тип процессора – мультиплексный канал прямого доступа во внутреннюю память, позволяющий осуществлять ввод, вывод по 24 дуплексным подканалам с суммарной скоростью 7 Мбайт/с. К каждому подканалу можно подсоединить до шести однотипных внешних устройств.
Структура М-10 допускает два основных вида распараллеливания алгоритмов: во-первых, по n идентичным арифметическим процессорам, синхронно выполняющим одну и ту же операцию, во-вторых, по разнотипным параллельно работающим процессорам (физическим устройствам), в числе которых два арифметических устройства, два канала процессор-память, устройство управления, мультиплексный канал.
Список литературы
- Гливенко Е.В. О функциях k-значной логики. //Вопросы радиоэлектроники. – М., 1970. – Серия ЭВТ, № 9.
- Саконтикова Н.Н. Некоторые вопросы теории логических операторов. //Вопросы радиоэлектроники. – М., 1971. – Серия ЭВТ, № 9.
- Гливенко Е.В. О классах перестановок k-значной логики. //Вопросы радиоэлектроники. – М., 1971. – Серия ЭВТ, № 9.
- Петрова Г.Н. Метод распараллеливания вычислительных алгоритмов применительно к анализу изображений снимков пузырьковых камер. //Вопросы радиоэлектроники. – М., 1974. – Серия ЭВТ, № 8.
- Гливенко Е.В. О взаимосвязи архитектуры многопроцессорных систем и параллельных алгоритмов //Вопросы радиоэлектроники. – М., 2003. – Серия ЭВТ, № 2.
Об авторах: РГУ нефти и газа им. И.М. Губкина, Москва
sergeypryadko@gmail.com
Материалы международной конференции SORUCOM 2011 (12–16 сентября 2011 года)
Статья помещена в музей 30.01.2012 с разрешения авторов
