Первые расчеты на ЭВМ М-2 нагрева баллистических ракет при движении их в атмосфере

Лавренюк Ю.А., Баженова Т.В.

Аннотация

Первые расчеты на ЭВМ М-2 нагрева межконтинентальных баллистических ракет при движении в атмосфере воздуха удалось произвести на создаваемой в лаборатории И.С. Брука ЭВМ М-2 в Энергетическом институте АН СССР (ЭНИН). В 1953 году в Энергетическом институте АН СССР были проведены численные расчеты c учетом термодинамики параметров потока воздуха за ударной волной (УВ) перед головной частью ракеты при температурах 200-20000 К и начальных давлениях от 1 до 10-5 атм. Пользуясь таблицами, можно по заданным значениям начального давления и скорости УВ определить параметры воздуха за прямым скачком уплотнения в передней критической точке. Результаты расчетов параметров воздуха за головной ударной волной перед головной частью ракеты немедленно передавались конструкторам из ОКБ  С.П. Королева, которые определяли необходимое количество теплозащитного материала. Расчет для идеального газа по баллистической траектории давал значения температуры 15 000 К Расчет с учетом термодинамики воздуха показал, что температура за скачком втрое меньше. Полученная информация позволила значительно снизить необходимое количество теплозащитного материала.

Необходимость расчетов

После окончания Великой отечественной войны США недолго оставалась монопольным обладателем ядерного оружия. Однако, для установления равновесия в мире нам необходимо было иметь не только бомбу, но и средства ее доставки через океан, тогда как военные базы США располагались и в Норвегии, и в Турции. При конструировании межконтинентальной баллистической ракеты возникла проблема теплозащиты. При гиперзвуковом обтекании ракеты перед ней возникает отошедшая ударная волна. (УВ) параметры которой на фронте вблизи передней критической точки практически совпадают с параметрами за прямым скачком уплотнения (рис. 1).

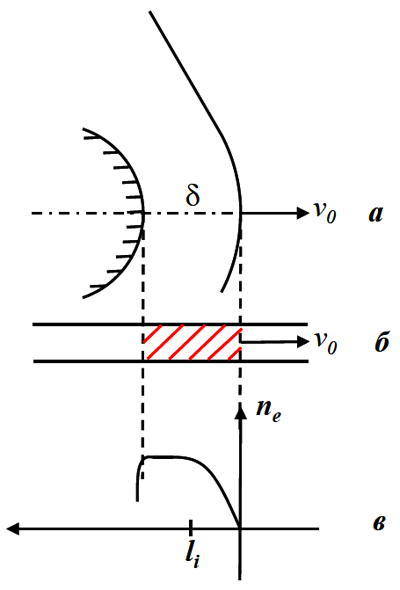
Скорость газа за УВ относительно тела падает от значений, определяемых по законам сохранения на фронте ударной волны, до нуля на теле. Параметры газа за прямым скачком уплотнения определяются законами сохранения массы, импульса и энергии. Эти законы связывают между собой параметры газа перед скачком с параметрами газа за скачком и со скоростью движения УВ.

Для определения температуры газа перед телом, движущейся с заданной скоростью, нужно использовать зависимость теплоемкости газа от температуры. В идеальном газе теплоемкость не зависит от температуры. Эта зависимость дается простым соотношением и система уравнений сохранения вместе с зависимостью энтальпии от температуры имеет аналитическое решение, связывающее параметры газа за скачком и перед скачком.

Оценки параметров воздуха за скачком по идеальной теории показали, что при скорости движения порядка 7 км/с температура в передней критической точке может достигать 15000 К (!). Это требовало такого количества теплозащитного материала, что ракета не могла бы подняться. Тогда ракетчики обратились к физикам с просьбой определить температуру за скачком в реальном газе. При высоких температурах при увеличении поступательной температуры часть энергии расходуется на возбуждение внутренних степеней свободы молекул (вращения, колебания, диссоциация, ионизация). Зависимость энтальпии газа от температуры вычисляется методами статистической физики и квантовой механики на основе экспериментальных данных об оптических константах молекул, характеризующих собственные частоты колебаний и вращений молекул. Расчет термодинамических параметров диссоциированного и ионизированного газа при высоких температурах требует численного решения системы алгебраических уравнений, связывающих состав газа с температурой и давлением по закону действующих масс через константу равновесия. Существовавшие к этому времени в США расчеты (таблицы Коппола) были выполнены. основываясь на неправильном значении энергии диссоциации азота. Расчеты, проводившиеся в СССР для оценки действия воздушной ударной волны ядерного взрыва, были проведены с большим интервалом по температуре (500 К). Расчет термодинамических параметров воздуха для определения количества теплозащитного материала должен был быть проведен для температур за скачком, меняющихся через каждые 100 К. Такой детальный расчет был необходим в связи с тем, что теплоемкость реального воздуха очень быстро изменяется с температурой и интерполяция могла привести к ошибочному определению температуры, а, следовательно, и необходимого количества теплозащитного покрытия.

Расчет параметров ударных волн в реальном воздухе

Соотношения между параметрами газа перед фронтом ударной волны и за ним определяется решением системы уравнений сохранения массы, импульса и энергии в частных производных. Для стационарного одномерного движения ударной волны уравнения приводятся к системе алгебраических уравнений:

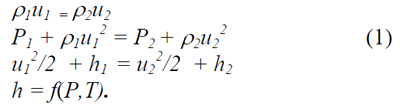
Здесь индексы 1 и 2 соответствуют начальному и конечному состоянию среды, P, ρ, u, h -давление, плотность, скорость и энтальпия соответственно.

В идеальном газе теплоемкость не зависит от температуры. Зависимость h (P,T) дается простым соотношением и система уравнений сохранения вместе с зависимостью энтальпии от температуры имеет аналитическое решение, связывающее параметры газа за скачком и перед скачком.

В газе при высоких температурах зависимость энтальпии от температуры является сложной, т. к. при увеличении поступательной температуры часть энергии расходуется на возбуждение внутренних степеней свободы молекул. Зависимость энтальпии газа от температуры вычисляется методами статистической физики и квантовой механики на основе экспериментальных данных об оптических константах молекул, характеризующих собственные частоты колебаний и вращений молекул.

Расчет термодинамических параметров реального газа при высоких температурах требует численного решения системы алгебраических уравнений, связывающих состав газа с температурой и давлением по закону действующих масс через константу равновесия. Сначала должны быть вычислены термодинамические функции компонент воздуха и значения констант равновесия, необходимые для расчета концентрации диссоциированныых и ионизированных молекул в зависимости от температуры. Для этого проводились вычисления статистических сумм для внутренних степеней свободы частиц на основе спектроскопических данных. Затем вычислялись состав и термодинамические функции воздуха при различных температурах и давлениях. Методом Ньютона-Рафсона решалась система нелинейных алгебраических уравнений для молярных долей компонент воздуха при каждой температуре и каждом давлении. Учитывалось 10 компонент. Для вычисления теплоемкостей решались две системы линейных уравнений для определения производной от числа молей при постоянном давлении и производных от числа молей при постоянном объеме. По данным решения трех систем и расчетам термодинамических функций компонент вычислялись термодинамические функции воздуха.

Расчеты параметров воздуха за ударной волной на ЭВМ М 2

Для определения газодинамических и термодинамических величин потока воздуха за прямым скачком уплотнения перед телом, входящим в атмосферу Земли численным методом решалась система уравнений (1), дополненная уравнениями состояния с учетом термодинамики реального воздуха.

Сначала расчеты проводились на 1 Московской фабрике механизированного счета вручную на «Мерседесах», но вскоре выяснилось, что необходимый объем работы может быть выполнен в срок только при помощи цифровой ЭВМ. В те годы, когда в СССР создавались первые в мире межконтинентальные ракеты, в стране действовала только одна БЭСМ-1, которая вплотную была занята ядерщиками. Необходимые расчеты удалось произвести на создаваемой в лаборатории И.С. Брука ЭВМ М-2 в Энергетическом институте АН СССР. Машина эта разрабатывалась в строгом секрете и ученые соседней лаборатории А.С. Предводителева, проводившие расчеты, узнали о её существовании благодаря счастливой случайности. Молодые сотрудники ЭНИНа вместе ходили в походы. Сотрудники Брука принесли Т.В. Баженовой в день рождения в подарок баночки с мазью для горных ботинок, завернутые в использованную бумажную распечатку отладочных расчетов на ЭВМ. К этому времени Т.В. Баженова уже имела понятие о том, как получаются подобные распечатки, и секрет их деятельности был раскрыт. Тогда парторги двух лабораторий обратились к руководству Института и было принято решение провести расчеты на ЭВМ М-2. Руководил эксплуатацией ЭВМ один из создателей этой машины Ю.А. Лавренюк. Разработка ЭВМ М-2 проводилась под руководством М.А. Карцева с участием Т.М. Александриди, В.В. Белынского, А.Б.. Залкинда, Ю.А. Лавренюка, Л.С. Легезо, В.Д. Князева, А.И. Щурова. Правительственное задание было выполнено в срок. Результаты расчетов параметров воздуха за ударной волной немедленно передавались конструкторам из ОКБ С.П. Королева, которые определяли необходимое количество теплозащитного материала.

Результаты расчётов

С учетом термодинамики воздуха проведены численные расчеты параметров потока воздуха за прямым скачком уплотнения при температурах 200-6000 К и начальных давлениях от 1 до 10-5 атм. Таблицы составлены для трех значений начальной температуры: 200, 300, 400 К, т. к. температура атмосферы Земли меняется с высотой. Термодинамические параметры воздуха приведены в таблицах для температур за скачком, меняющихся через каждые 100 К. Для каждого значения температуры вычислены скорость УВ, за которой создается такая температура при данном начальном давлении, а также термодинамические параметры (давление, энтальпия, энтропия, скорость звука и эффективный показатель адиабаты). Во второй части таблиц термодинамических функций приведены удельные концентрации продуктов диссоциации воздуха xi.

Пользуясь таблицами, можно по заданным значениям начального давления и скорости УВ определить параметры диссоциированного воздуха за прямым скачком уплотнения в передней критической точке (рис. 1). Отличие от идеального газа особенно сильно проявляется с уменьшением атмосферного давления на больших высотах полета.

С учетом термодинамики воздуха в 1953 году в Энергетическом институте АН СССР были проведены численные расчеты параметров потока воздуха за прямым скачком уплотнения при температурах 200-20000 К и начальных давлениях от 1 до 10-5 атм. Впоследствии таблицы были пересчитаны в ВЦ АН СССР и изданы в 1962 году [1.-4].

Параметры воздуха в области за отошедшей УВ рассчитаны численными методами [5]. Расстояние отхода ударной волны δ от передней критической точки тела с радиусом кривизны r0 может быть аппроксимировано формулой δ /r0 = 0,78 ρo/ ρ 1 , где ρo и ρ1 - плотности воздуха до скачка и после скачка. С помощью таблиц газодинамики величину ρo/ ρ 1 можно выразить через высоту Н и скорость полета тела vo . Эта связь аппрокисимруется следующими выражениями:

при 20 ≤ Н ≤ 80 км, S ≤ vo ≤ 9 км/с ,
δ /r0 = 0,08 exp ( - 0,083 (vo - 3) - 3. 104 ( H - 22,2);
при 0 < Н < 30 км, 2 < vo < 7 км/с,
δ / r0 = (Н + 1) / vo exp ( 1,14 . 104 vo + B( H ));
B( H) = 1.48.10-2 H2 - 0,412 H + 5,37 при 0 ≤ H ≤ 15 км,
B( H) =3.97 .10-4 H2 - 0.78 H + 3,6 при 15 ≤ H ≤ 30 км.

Сжатый и нагретый УВ воздух вытекает из области вблизи передней точки тела в боковую область. При этом поток расширяется и охлаждается. УВ ослабляется волнами разрежения и превращается в косой скачок уплотнения, который поворачивает набегающий поток параллельно образующей конуса. Повышение температуры и давления за косым скачком незначительно, но скорость потока относительно тела за косым скачком в отличие от прямого скачка становится соизмеримой со скоростью набегающего потока. Распределение температуры по нормали к оси конуса неоднородно, т. к. вблизи стенки движется слой из энтропически расширяющегося нагретого газа из области за прямым скачком, а на некотором расстоянии от стенки он сливается с потоком, прошедшем через косую УВ. Численный расчет обтекания затупленных конусов реальным воздухом с помощью таблиц термодинамики выполнен методом характеристик. Результаты расчета приведены в таблицах [6] .

Пользуясь таблицами [1–4] можно по заданным значениям начального давления и скорости УВ определить параметры воздуха за прямым скачком уплотнения в передней критической точке (рис.2).

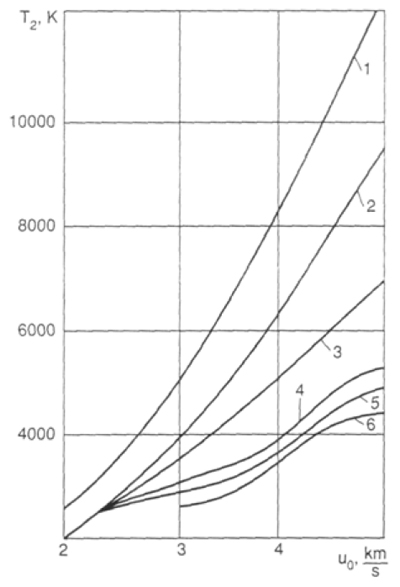
Рис. 2. Температура воздуха за головной ударной волной при движении тел в атмосфере в зависимости от скорости. 1 – идеальный газ, 2 – учет возбуждения колебаний, 3-6 – учет диссоциации и ионизации на высотах от 0 до 80 км.

При спуске по баллистической траектории с изменением высоты от 80 до 15 км скорость медленно уменьшается от 6,7 до 6,1 км/с. Температура за скачком растет с увеличением атмосферного давления от 5400 до 8000 К. Отличие от идеального газа особенно сильно проявляется с уменьшением атмосферного давления на больших высотах полета. Расчет для идеального газа давал значения температуры 15 000 К независимо от высоты. Полученная информация позволила значительно снизить необходимое количество теплозащитного материала, что обеспечивало решение проблемы теплозащиты межконтинентальной баллистической ракеты.

Список литературы

1. Предводителев А.С., Ступоченко Е.В., Плешанов А.С., Самуйлов Е.В.,Рождественский И.Б. Таблицы термодинамических функций воздуха для температур от 6000 до 12000 К и давлений О,00001 до 100 атмосфер для температур от 12000 до 20000 К. М: Изд. АН СССР, 1957.
2. Предводителев А.С., Ступоченко Е.В., Плешанов А.С., Самуйлов Е.В., Рождественский И.Б. Таблицы термодинамических функций воздуха для температур от 12000 до 20000. К и давлений от 0,001 до 1000 атмосфер. М.: Изд. АН СССР, 1958.
3. Предводителев А.С., Ступоченко Е.В., Плешанов А.С., Самуйлов Е.В., Рождественский И.Б.. Таблицы термодинамических функций воздуха. Ч. 1 - для температур от 200 до 6000 К и давлений О,00001 до 100 атмосфер. М.:, ВЦ АН СССР, 1962
4. Предводителев А.С., Ступоченко Е.В., Рождественский И.Б., Самуйлов Е.В., Плешанов А.С. Таблицы газодтнамических и термодинамических и величин потока воздуха за прямым скачком уплотнения. Ч. 1,2 и 3. М.: ВЦ АН СССР, 1962
5. Белоцерковский О.М. Обтекание затупленных тел сверхзвуковым потоком газа .М.: ВЦ АН СССР, 1968
6. Лунев В.В., Магомедов К.М., Павлов В.Г. Гиперзвуковое обтекание притупленных конусов с учетом равновесных физико-химических превращений. М.: ВЦ АН СССР, 1968

Об авторах: Институт проблем информатики РАН
lavr1@voxnet.ru
Институт высоких температур РАН, Москва

Материалы международной конференции SORUCOM 2011 (12–16 сентября 2011 года)
Статья помещена в музей 11.10.2011 с разрешения авторов