Уравновешенная троичная система счисления и Томас Фаулер

В. В. Шилов

Привычная и кажущаяся нам сегодня столь естественной десятичная система счисления отнюдь не сразу утвердилась в качестве основной, используемой человеком. Например, в книге историка математики Дирка Стройка [4, с. 23] со ссылкой на работу [17] говорится о 307 известных системах счисления только лишь первобытных народов американского континента, из которых десятичными были менее половины, а именно 146. Поэтому не удивительно, что первые устройства, предназначенные для облегчения счёта, не были десятичными: в частности, древнегреческий абак был основан на двоично-пятиричной системе счисления. А в древнеримском абаке для действий с целыми числами использовалась десятичная система, в то время как при работе с дробными числами складывались двенадцатые (унции), а также двадцать четвертые (половина унции), сорок восьмые (четверть унции) и семьдесят вторые (шестые части унции) части. И тот, и другой вид абака были предназначены в первую очередь для денежных подсчетов, и отражали поэтому особенности соответствующих денежных систем.

То же самое можно сказать и о гораздо более поздних счётных приборах и вычислительных устройствах. Например, в построенной в 1642 г. машине Блеза Паскаля (1623-1662) значения разрядов складываемых чисел представлялись углами поворота зубчатых колес. Шесть из них соответствовали сумме в ливрах и имели по десять зубцов, а два правых, соответствовавших более мелким денежным единицам – су и денье, имели 20 и 12 зубцов. Точно так же не были чисто десятичными сумматоры Буратини [1] (1659 г.) и Сэмюэла Морленда [2] ( 1666 г.). Тем не менее, всё-таки именно десятичная система почти на три столетия стала основой построения инструментальных средств вычисления.

Но даже после окончательного утверждения десятичной системы, в повседневной жизни людей во многих случаях все-таки применялись и другие системы счисления. Это было связано в первую очередь с продолжавшимся широким использованием традиционных систем мер и весов. (Напомним также, что шестидесятеричную систему, следуя традиции, восходящей к Древнему Вавилону и античности, использовали для вычислений астрономы.) При этом внимание математиков, начиная с XVII в., стали привлекать различные системы счисления с основаниями, отличными от 10. Около 1600 г. двоичную систему счисления предложил Томас Гарриот [3] (правда, об этом не было известно вплоть до появления в 1951 г. работы [35]). Паскаль в написанном в 1654 г. и опубликованном посмертно спустя одиннадцать лет сочинении “ De numeris multiplicibus ex sola characterum numericorum additione agnoscendis ” (“О делимости чисел, выведенной только лишь с помощью сложения их цифр”) высказывал мнение, что основанием системы счисления может быть любое положительное число. Он писал, что десятичная система построена не слишком разумно, поскольку следует “людским обычаям”, а не требованиям “естественной необходимости”, и предлагал перейти к двенадцатеричной системе счисления. В 1670 г. испанский епископ Хуан Карамюэль (1606-1682) опубликовал работу “ Mathesis biceps vetus et nova ” (“Два лика математики – новой и старой”), в одной из частей которой рассмотрел системы счисления с основаниями 2, 3, 4, 5, 6, 7, 8, 9, 10, 12 и 60.

Начиная с 1697 г. в письмах к разным адресатам (герцогу Брауншвейгскому Рудольфу Августу, Иоганну Кристиану Шуленбургу, Иоганну Бернулли, иезуиту отцу Буве) выработанные им принципы двоичной арифметики неоднократно излагал великий немецкий учёный Готфрид Вильгельм Лейбниц (1646-1716). После появления в 1703 г. статьи Лейбница [30], в которой объяснялись правила двоичной арифметики, именно двоичная система приобрела наибольшую известность. Правда, Лейбниц не считал, что её необходимо применять на практике, он рассматривал двоичную систему в основном как важный инструмент теоретических исследований. Заметим, что в работе [2] было показано, что впервые продемонстрировал огромные потенциальные возможности применения двоичной системы для вычислений ещё изобретатель логарифмов Джон Непер (1550-1617), в 1617 г. предложивший свою “счётную доску” [4].

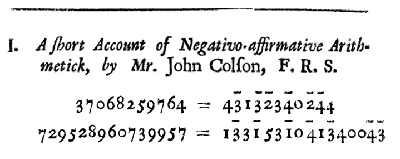
Рис.1 Запись чисел по системе Д. Колсона

В 1726 г. кембриджский математик Джон Колсон (1680-1760) [13] предложил использовать десятичную позиционную систему счисления как с положительными, так и с отрицательными цифрами (рис. 1). Колсон привёл многочисленные примеры выполнения арифметических операций над записанными в его системе числами, и высказал мнение, что они являются менее трудоёмкими, чем вычисления с использованием обычной записи, особенно если эти числа большие. В конце статьи Колсон отметил, что отрицательные цифры можно использовать также для записи чисел и упрощения вычислений в двенадцатеричной, шестидесятеричной и других системах счисления [5].

Прошло более ста лет, прежде чем на системы с цифрами разных знаков обратил внимание знаменитый французский математик Огюст Коши (1789-1857). Он предложил использовать десятичную систему с десятью цифрами от -4 до 5; так, в его записи число 8256 принимает вид 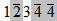[11]. В такой “сокращённой”, по сравнению с системой Колсона, записи легче заметить симметричность цифр. Возможно, что именно по этой причине в том же 1840 г. французский инженер и изобретатель аналоговых счётных инструментов Леон Лаланн (1811-1892), развивая идею Коши, опубликовал описание уравновешенной (или симметричной ) троичной системы [29], в которой имелись только три цифры.

Однако, строго говоря, работа Лаланна первой всё-таки не была. Так, ещё в 1811 г. английский математик Питер Барлоу (1776-1862), описывая разные системы счисления, показал в одном из примеров, что десятичное число 716 в троичной системе будет равно 222112, или же 3⁶ -(3² +3+1) [8, с. 240]. Если ввести обозначение вместо -1 (правда, сам Барлоу этого не сделал), то последняя запись примет вид (1000 )₃. Сегодня по аналогии с битами двоичной системы счисления разряды чисел в такой записи называют тритами. Приведённый Барлоу пример был связан с решением задачи на взвешивание, однако известно, что неявное представление чисел в уравновешенной троичной системе присутствует ещё в известной “задаче Баше [6] о весах”, которую, в свою очередь, Фибоначчи (ок. 1170-ок. 1250) сформулировал за 400 лет до Баше. В этой задаче требуется найти набор из четырёх гирь, с помощью которого можно взвесить любой груз весом от 1 до 40 кг (в другом варианте задачи - трёх гирь для взвешивания любого груза весом от 1 до 13 кг ). Пусть, например, надо взвесить груз в 33 кг . Представим число 33 в уравновешенной троичной системе: 33=27+9 - 3+0=11 0₃. Значит, на одну чашку весов надо положить гири 27 кг и 9 кг , а взвешиваемый груз и гирю 3 кг - на другую. Если к этим трём гирям добавить ещё одну, весом 1 кг , то мы сможем взвесить любой груз, не превышающий 40 кг. Фактически для решения задачи надо просто найти представление в уравновешенной троичной системе целого числа, равного весу груза.

Приведём ещё несколько примеров записи чисел в уравновешенной троичной системе счисления:

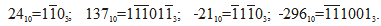
Легко заметить, что уравновешенная троичная система счисления обладает многими весьма привлекательными свойствами. Прежде всего, знак числа определяется первым ненулевым символом в его троичной записи: если это 1, то число положительное, а если , - то отрицательное. Очень просто перейти к противоположному числу, заменив 1 на и наоборот. В самом деле:

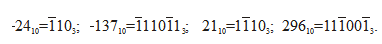
Теперь запишем в уравновешенной троичной системе несколько дробных чисел:

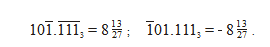
Для округления троичного числа до ближайшего целого достаточно отбросить его дробную часть. Это свойство также достаточно очевидно, поскольку самая большая возможная положительная дробная часть, 0.111...₃, представляет сумму 1/3+1/9+1/27..., которая всегда меньше, чем 1/2 (а соответственно, самая большая по модулю отрицательная дробная часть, 0.... ₃, всегда больше, чем1/2).

Очень просто выполняется в уравновешенной троичной системе сложение. Составим таблицу сложения, которой будем пользоваться для обычного сложения чисел столбиком:

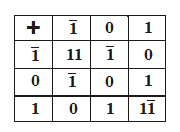
Например, при сложении + получаем 1, а в следующий разряд переносим . Сложим записанные в уравновешенной троичной системе числа 296 и 137:

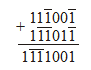
Легко проверить, что результат действительно равен 433. Столь же просто производится и вычитание: для этого достаточно изменить знак вычитаемого на противоположный и сложить с уменьшаемым.

Запишем теперь таблицу умножения:

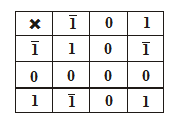
Умножим с её помощью записанные в уравновешенной троичной системе числа 20 и - 19:

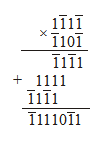
Результат равен –380, при этом нетрудно заметить, что умножение сводится к простым операциям изменения знака и сложения.

После Лаланна уравновешенная троичная система практически не привлекала внимания учёных [3, с. 218] [7]. Во второй половине 1940-х гг. на смену ранним механическим и электромеханическим вычислительным устройствам, основанным на десятичной системе счисления, стали приходить электронные компьютеры, и на авансцену вышла двоичная система счисления. Её использование для тогдашней элементной базы являлось наиболее естественным, однако некоторое время в качестве альтернативы десятичной всерьез рассматривалась также и уравновешенная троичная система. Например, о ней известный американский специалист Герберт Грош (р. 1918) вспоминает, как однажды в 1949 г. в разговоре с главным конструктором компьютера “Whirlwind” и изобретателем памяти на ферритовых сердечниках Джеем Форрестером (р. 1918) сказал, что по-настоящему серьёзного прорыва можно было бы добиться, храня в каждом сердечнике один троичный разряд, и ведя вычисления не в двоичной, а в уравновешенной троичной системе [26, с. 151-152] [8]. В 1950 г. о троичной системе писали авторы монографии [27] и создатель теории информации Клод Шеннон (1916-2001) [34]. Причина этого интереса понятна. Мы уже видели, что арифметические операции над числами, записанными в этой системе, выполняются очень просто. Но она обладает и другими достоинствами: запись числа в ней существенно короче, чем при использовании двоичной системы (требуется лишь 63% позиций), нет необходимости использовать специальный знаковый разряд. Кроме того, значительно упрощается схемная реализация арифметики, поскольку отпадает необходимость анализировать знаки операндов.

Дональд Кнут писал в 1969 г., что время троичной арифметики в компьютере наступит в будущем, если удастся заменить триггер, позволяющий хранить один бит информации, элементом, позволяющим хранить один трит [3, с. 219]. Однако, как теперь хорошо известно, задолго до выхода его книги уравновешенная троичная система счисления уже была успешно применена в крайне интересной и оригинальной отечественной разработке. Речь идёт об ЭВМ “Сетунь” [1], которая была создана в Вычислительном центре МГУ в 1959 г. Н.П. Брусенцовым. Начиная с 1962 г. машина выпускалась серийно, и за три года были изготовлены около 50 экземпляров.

Схемы “Сетуни” строились на электромагнитных пороговых логических элементах, в которых входы имели положительные и отрицательные веса, а значения 1, и 0 соответствовали положительному, отрицательному и нулевому току. Устройства “Сетуни” на базе троичной арифметики оказались не только более простыми и быстрыми, они также потребляли меньшую мощность, чем двоичные устройства, реализованные на тех же элементах.

Это была машина с фиксированной запятой, операции с плавающей запятой реализовывались программно. Система команд насчитывала всего 24 команды (среди них три команды условного перехода и команда умножения тритов), но, используя их, можно было эффективно программировать самые разные задачи. Память была двухуровневой: оперативная память на ферритовых сердечниках объёмом 162 коротких слова (9 тритов) и основная память на магнитных барабанах объёмом 3888 коротких слов. Время выполнения сложения и вычитания составляло 180 мкс , а умножения - 320 мкс . В то время “Сетунь” превосходила другие малые машины по производительности, при этом она была значительно дешевле машин своего класса и отличалась очень высокой надёжностью. Спустя несколько лет, в 1970 г., был построен экспериментальный образец усовершенствованной машины “Сетунь 70” . Она отличалась рядом интересных архитектурных особенностей, а идея применения трёхзначной логики получила в ней дальнейшее развитие.

Длительное время считалось, что проект “Сетунь” является единственным примером использования троичной системы в вычислительной технике, однако недавние архивные открытия изменили это представление. Оказалось, что первая попытка построить троичную механическую вычислительную машину была предпринята ещё в середине XIX в.

* * *

Томас Фаулер родился в 1777 г. в Большом Торрингтоне, что в Северном Девоншире - в этом городке пройдет и вся его жизнь. Его родители, бондарь Хью и Элизабет, с трудом сводили концы с концами, и в тринадцатилетнем возрасте Томас был отдан подмастерьем к торговцу кожами. Пусть обычно в те времена дети из бедных семей начинали работать в гораздо более раннем возрасте [9], - такой жизненный старт всё же сулил мало хорошего. И если Фаулер в конце концов удалось добиться в жизни определённого положения, то этим он был всецело обязан своей жадной тяге к знаниям. Вероятно, только благодаря ей Томас сумел всё-таки получить начальное образование [10].

Особенно Фаулера привлекала математика, которую он изучал самостоятельно по известному в свое время учебнику Джона Варда, выдержавшему в XVIII столетии полтора десятка изданий: “После тягот дневной работы среди овчин он проводил половину ночи, углубившись в учебник математики, и дошёл таким образом до флюксий мастера Сондерсона [11], под каковым названием был тогда известен метод дифференциального исчисления. Не нашлось никого, увы! чтобы принять в нём участие и помочь продолжить обучение в Кембридже, где единственно талант, каковым он несомненно обладал, мог полностью развиться и быть оценённым по достоинству, так что он оставался без помощи и сочувствия в своих уединенных занятиях”, - спустя много лет написал его сын, преподобный Хью Фаулер. (Следует сказать, что большая часть известных сегодня подробностей жизни Томаса Фаулера дошла до нас именно благодаря Хью Фаулеру, напечатавшему в 1875 г. биографический очерк об отце [18]).

Тем не менее, стремление изменить свою судьбу и выбиться из нищеты, соединенные с исключительным трудолюбием и выдающимися способностями, позволили Фаулеру около 1800 г. начать карьеру печатника (он издал впоследствии несколько небезынтересным книг) и торговца книгами. В 1813 г. он женился на местной жительнице Мэри Копп; у них было по меньшей мере одиннадцать детей (несколько из них умерли ещё в раннем возрасте).

Рис. 2. Т. Фаулер. Титульный лист брошюры с описанием термосифона. 1829

Несмотря на необходимость обеспечивать средствами к существованию немалое семейство, Фаулер постоянно занимался самообразованием и на всю жизнь сохранил тягу к науке. С печатным делом связано одно из его изобретений – печатный пресс, который он сам же и изготовил. Однако первым “официально признанным” результатом Фаулера стало устройство, которое сам он назвал термосифоном и на который получил 20 октября 1828 г. патент за № 5711 [36, 38]. Вскоре Фаулер издал брошюру с его описанием [19] (рис. 2).

Фаулер рассчитывал, что изобретение станет основой его благосостояния. Но на деле оно лишь явилось причиной жесточайшего разочарования. Сын Фаулера сетовал: “К сожалению, его изобретение было вскоре растащено во все стороны. Единственным средством борьбы были дорогостоящие судебные разбирательства, но имей даже он средства для их ведения, успех был бы сомнителен…” [12].

Однако никак нельзя сказать, что от борьбы Фаулер отказался. Сначала он попытался обратиться к прессе. Так, напечатал в журнале “Gardener's Magazine” письмо [31], в котором протестовал против данной в этом издании характеристики работы другого изобретателя, мистера Кьюли (Kewley), как “важнейшего улучшения” систем водяного отопления. По мнению Фаулера, изобретение Кьюли было всего лишь незначительным улучшением его собственной системы и нарушало его патентные права. Ответ редактора был весьма обескураживающим – тот, оговорившись, что плохо знает патентное право, писал, что на его взгляд, после публикаций маркиза де Шабанна [13] в этой области вообще нет предмета для патентования кем-либо – будь то Фаулер, Кьюли или кто другой… [31, с. 378]. В самом деле, общие принципы построения таких систем к середине 1820-х гг. были уже известны. Однако на практике их успех в решающей степени зависел от понимания некоторых сугубо инженерных тонкостей и умения воплотить их в техническое устройство. И, например, де Шабанн таким умением (в отличие от того же Кьюли, которого современный ему источник характеризует как талантливого инженера с основательной научной подготовкой) не обладал.

Не добившись понимания у специалистов и доведенный до отчаяния, Фаулер обратился за помощью к власть имущим. 22 января 1834 г. он направил письмо лорду-канцлеру лорду Брогему, прося его светлость рассмотреть дело, из-за нерешённости которого он “в гневе и разочаровании” возвращается из столицы домой к своей “почти голодающей семье”. В том же письме Фаулер настаивал на изменении патентных законов с тем, чтобы “предотвратить полное разорение искусного [в технике] бедняка, ставшее единственной наградой за его искусство” (цит. по [25, с. 5]).

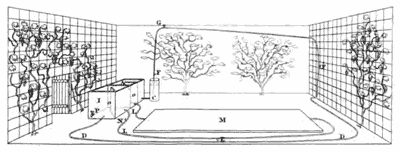
Рис. 3. Т. Фаулер. Схема обогрева оранжереи. Рис. из брошюры

Борьба Фаулера не принесла результата. О причинах этого сегодня трудно судить, ? впрочем, как и о том, насколько на самом деле его изобретение было удачным и практичным. С одной стороны, изобретение на весьма актуальную в то время тему было замечено печатью [14], с другой – эти отклики никогда не были слишком восторженными. А главное – изобретение Фаулера не выдержало проверки временем. Спустя четверть века в посвященной системам отопления монографии Чарльза Гуда работа Фаулера была удостоена лишь нескольких, причём не самых лестных слов. По мнению автора монографии, система отопления Фаулера была “совершенно неприменима для заявленной цели вследствие сложной системы труб и кранов, необходимой для её работы; эта проблема была полностью устранена в изобретении м-ра Кьюли” [28, с. 142]. А вот систему Кьюли Гуд описывает во всех деталях [28, с. 121-123]. Точно так же в капитальном двухтомном труде Уолтера Бернана, посвящённом истории развития систем отопления и вентиляции с древности до середины XIX в., система Кьюли характеризуется положительно, а система Фаулера даже не упоминается [9, с. 274]. Таким образом, похоже, что она всё-таки оказалась не слишком практичной. Косвенно о том же свидетельствует и тот факт, что спроектированные Фаулером системы обогрева помещений были установлены лишь в одном из окрестных поместий, а также в теплице для выращивания винограда (рис. 3). О других заказах на их установку ничего не известно, в то время как система Кьюли получила широкое распространение по всей стране. Заметим также, что свою первую отопительную систему Кьюли установил ещё в 1826 г., т. е. до появления работы Фаулера [15].

В любом случае, Фаулер был крайне удручён своим, столь неудачным, опытом изобретательства, и это, как мы увидим, имело серьёзные последствия для истории вычислительной техники.

Тем временем к середине 1830-х гг. социальный статус Томаса Фаулера значительно упрочился, - он стал управляющим единственного банка в городе и даже партнёром его владельцев. Об изменившемся общественном положении Фаулера со всей очевидностью свидетельствует также его назначение в 1835 г. казначеем административной структуры, созданной согласно Закону о бедных (Poor Law). Этот закон, принятый в 1834 г., модифицировал (в первую очередь централизовал) всю систему общественного призрения. Ответственность за оказание помощи всем нуждающимся в ней возлагалась на округа (или унии), объединявшие от 20 до 30 приходов.

Задача, которую приходилось решать Фаулеру (как и казначею любого другого округа), заключалась в следующем. Известен общий размер S налога, который округ должен собрать, складывающийся из налогов S i , собираемых в каждом приходе. Часть этой суммы C остается в округе как компенсация различных административных расходов и должна быть распределена между приходами пропорционально их вкладу в сумму налогового сбора по округу. Тогда долю каждого прихода можно определить как величину Ci=C*(Si/S). Эти вычисления составляли одну из обязанностей казначея.

Британская денежная система в то время была достаточно сложной: один фунт стерлингов равнялся 20 шиллингам, шиллинг – 12 пенсам, а пенни – 4 фартингам (таким образом, в одном фунте содержится 960 фартингов). Поэтому для удобства вычислений все денежные суммы Фаулер приводил к самой мелкой единице – фартингу, и вёл расчеты в десятичной системе над получающимися в результате приведения достаточно большими целыми десятичными числами. Таким образом, казначей должен был выполнить следующие действия: выразить все S i , а также S и C в фартингах; вычислить пропорции Si/S и умножить каждый результат на C; преобразовать каждое Ci из фартингов в фунты.

Рис. 4. Т. Фаулер. Титульный лист таблиц. 1838

*** Эти действия включают множество операций умножения и деления. Например, округ Фаулера состоял из 23 приходов, поэтому казначей должен был выполнить 25 преобразований из фунтов в фартинги и 23 обратных преобразования, а также по 23 умножения и деления больших десятичных чисел. Не надо забывать также, что казначей регулярно повторял свои расчёты, поэтому любое сокращение количества операций и их трудоёмкости могло значительно упростить его работу.

Большой объём и утомительный характер вычислений привели Фаулера к мысли попытаться облегчить их, и он нашёл остроумное решение проблемы, значительно упростив процесс вычислений посредством использования специальных таблиц. Фаулер воспользовался тем, что “любое число может быть представлено в виде комбинации степеней 2 или 3” . В 1838 г. в Лондоне были изданы составленные им “Таблицы для облегчения арифметических вычислений” [20] (титульный лист книги показан на рис. 4). Их первая часть содержала таблицу коэффициентов при степенях двойки в двоичном представлении чисел от 1 до 130048. Вторая часть была таблицей представлений чисел от 1 до 3985807 в уравновешенной троичной системе (таким образом, можно констатировать, что Фаулер предложил уравновешенную троичную систему ранее Лаланна; при этом он не знал о работах Баше и Барлоу, и считал её своим изобретением).

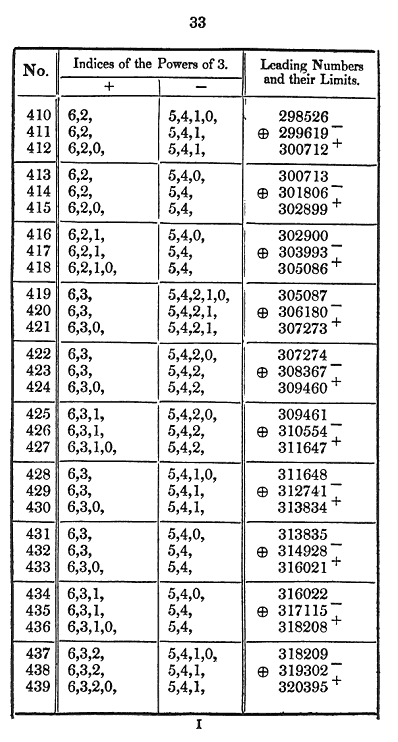
Рис. 5. Т. Фаулер. Таблицы (с. 33)

Для каждого десятичного числа (крайний левый столбец, см. рис. 5) его представление в уравновешенной троичной системе задается в двух следующих столбцах номерами позиций цифр 1 и (на самом деле Фаулер использовал обозначения “+” и “ - ” соответственно, но для простоты мы далее будем придерживаться современной нотации). Например, число 420 записывается как 1 10 (т.е. цифра 1 стоит в шестой и третьей позициях, - в пятой, четвёртой, второй и первой, и 0 - в нулевой). Кроме того, имеется ещё один (крайний правый столбец), в каждой клетке которого записаны три числа. Среднее из них может быть представлено в уравновешенной троичной системе путём добавления 6 к номеру позиции каждой цифры числа из левой колонки. Например, для числа 306180, находящегося в той же строке, что и 420, это 1 10000000 (т. е. цифра 1 стоит теперь в двенадцатой и девятой позициях, - в одиннадцатой, десятой, восьмой и седьмой, и 0 - в шестой и во всех остальных). Числа над и под ним задают диапазон, в котором действует равное 6 смещение (в данном случае – от 305087 до 307273). Это означает, что троичное представление любого целого числа N I [305087, 307273] может быть получено с помощью таблицы, - для этого достаточно взять троичное представление числа 306180 и прибавить (или вычесть) взятое из левого столбца таблицы троичное представление разности между числами 306180 и N.

Таблицы Фаулера создавались в расчёте на решение конкретной задачи, поэтому вполне объясним подзаголовок книги: “Предназначены для вычисления пропорциональных выплат по приходам округа Закона о бедных”. Помимо общих сведений об уравновешенной троичной системе, правил выполнения арифметических операций над ними и соответствующих примеров, в одном из разделов книги Фаулер дал подробное описание процесса вычислений с их использованием.

Предполагая, что величины S, Si и C известны, он строит вспомогательную таблицу, в которой приведены рассчитанные им величины сумм, подлежащих распределению в приходе, накладные расходы в котором составляют величину, в точности равную степени тройки: 1, 3, 9, 27, 81, 243, 729, 2187 и т.д. фунтов стерлингов. При этом результат указывается уже в окончательной форме (фунты, шиллинги, пенсы).

Правила пользования таблицей Фаулер объяснил на примере. Пусть налогообложение округа составляет 7416 фунтов , налог с гипотетического прихода 729 фунтов , а накладные расходы округа – 177 фунтов стерлингов, 2 шиллинга и полтора пенса. Согласно соотношению Ci=C*(Si/S), Фаулер вычисляет сумму накладных расходов гипотетического прихода (см. рис. 6), ведя при этом все вычисления в фартингах. Эта величина составляет 16713.33 фартинга, или 17 фунтов 8 шиллингов и 2 с четвертью пенса (с остатком 0.33 фартинга) и соответствует 6-й степени тройки в таблице.

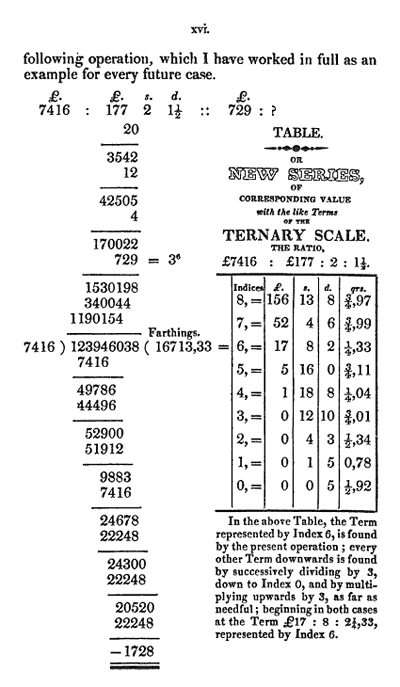
Рис. 6. Т. Фаулер. Таблицы (с. xvi)

Если же величина накладных расходов прихода не составляет точной степени тройки, то действовать следует так. В таблице находится троичное представление соответствующего числа (в одном из примеров, рассмотренных Фаулером, это 1207 фунтов стерлингов, троичное представление этого числа равно 10001). Теперь достаточно сложить взятые из вспомогательной таблицы суммы, соответствующие цифре 1, и вычесть суммы, соответствующие цифре , т.е. сложить суммы, соответствующие индексам 7 и 0 и вычесть суммы, соответствующие индексам 6, 5 и 2. В результате получим, что искомая величина накладных расходов прихода равна 28 фунтам , 16 шиллингам и 6 пенсам с остатком 0.13 фартинга.

Если округ состоит из 23 приходов, то потребуется всего 9 преобразований из фунтов в фартинги и обратно, 2 деления больших чисел (троичных), 6 делений на 3, 2 умножения на 3 и вычисление 23 сумм (по одной для каждого прихода, не более чем 7 слагаемых).

Таким образом, Фаулеру удалось устранить из расчётов наиболее трудоёмкие операции умножения и деления. И хотя при этом появляются накладные расходы на составление вспомогательной таблицы, при её наличии вычисления сводятся к сложениям и вычитаниям. Получающиеся результаты непосредственно выражают денежные суммы, подлежащие распределению в каждом приходе, благодаря чему устраняются также фазы перевода денежных сумм в десятичную систему и обратно. Кроме того, выигрыш становится более значительным для больших округов.

Тем не менее, вполне очевидно, что для вычислений, не носящих регулярного характера, описанный метод значительного эффекта все-таки не даёт. Это обстоятельство заставило Фаулера обратиться к мысли попытаться механизировать вычисления, и уже спустя два года после издания таблиц он сконструировал и построил свою механическую вычислительную машину. Несомненно, что она первоначально она была предназначена для выполнения тех же специфических вычислений, связанных с расчетами по Закону о бедных, – именно этим объясняется то, что машина работала в уравновешенной троичной системе счисления и предназначалась для выполнения операций умножения и деления [16]. Впервые свою машину Фаулер показал в мае 1840 г. Чарльзу Бэббиджу и Фрэнсису Бофорту [17], а затем группе членов Лондонского Королевского общества.

Несомненно, машина их заинтересовала. Фаулеру предложили представить её описание, чтобы включить рассмотрение машины в повестку дня очередного заседания Королевского общества. Такое описание было составлено выдающимся математиком и логиком Августом де Морганом (1806-1871), ? несмотря на свою краткость, оно до сих пор остается самым подробным описанием троичной машины Фаулера [15] (опубликовано было только краткое изложение описания де Моргана [16]). Согласно ему, машина состояла из четырёх основных частей: первая, вторая и третья предназначены для представления множимого, множителя и произведения (или делимого, делителя и частного) соответственно. Четвёртая часть – это механизм переноса. После установки значений сомножителей раму множителя следовало сдвинуть в плоскости, перпендикулярной плоскостям множимого и произведения, и благодаря, зацеплению реек трёх частей машины, получить результат.

Спустя некоторое время в письме к тогдашнему королевскому астроному профессору Джорджу Айри (1801-1892) Фаулер написал: “Эта Машина была построена полностью моими собственными руками (преимущественно из дерева) с крайней заботой об экономии и исключительно с целью претворить мои Идеи относительно такого способа вычисления в некоторую материальную форму; она имеет длину приблизительно 6 футов , высоту один фут и ширину три фута. Будучи построена из меди и железа, она заняла бы места немного больше, чем небольшое бюро, обладая при этом теми возможностями, о которых я написал”.

Профессор Айри был фактически научным советником британского кабинета, и судьба проекта во многом зависела от его мнения. Более того, он прекрасно понимал всю практическую важность проблемы вычислений и создания средств их механизации – ведь именно астрономы издавна отвечали в Англии за составление разнообразных навигационных таблиц для Адмиралтейства (см. напр., [14]).

Далее в письме Фаулера мы читаем: “Я имел честь в мае 1840 г. в Лондоне представить машину для осмотра многим Учёным Мужам, среди которых были маркиз Нортхэмптон, м-р Бэббидж, У.Ф. Бейли [18] и А. де Морган, эскв. и многие другие Достопочтенные и Благородные Господа, члены Королевского общества и др., и я с великим удовольствием воспринял бы также ваше мнение. Все они отзывались благожелательно о моем изобретения, но, - как бы непривычно это ни звучало - моим самым большим желанием было бы услышать вместо похвал полное научное исследование принципов Машины и деталей её устройства - и я надеюсь, что такое исследование людьми первого разряда науки ещё состоится прежде, чем изобретение мое будет отклонено или принято.

Я целиком отдаю отчёт в склонности людей переоценивать собственные изобретения и придавать неуместную важность предметам, безраздельно поглощающим их мысли, но я отважусь сказать, - и надеюсь, что буду полностью понят джентльменом, имеющим ваши научные достижения, - сколь часто меня изумляла красота полностью механических вычислений.

Я часто размышляю о том, что если бы во младенчестве человечества троичная система была избрана вместо десятичной, то машины, подобные представленной, уже вскоре стали бы привычными, поскольку переход от мысленных вычислений к механическим оказался бы так очевиден и прост.

Я весьма сожалею, что не могу предоставить вам какие-либо чертежи Машины, но надеюсь, что сумею показать её перед Британской ассоциацией [19] в Дэвенпорте в следующем августе, когда, как я смею надеяться и верю, смогу снова под покровительством вашей неоценимой помощи, вынести её на рассмотрение. Я вёл очень уединённую жизнь в своём городе, не имея возможности получить какую-либо помощь от кого бы то ни было, и я буду чувствовать себя потерянным среди столь многих ученых и выдающихся мужей, собравшихся на встречу, не имея доброго друга, ведущего меня и покровительствующего мне” [20].

Высказанные здесь Фаулером мысли о простоте механической реализации счёта, основанного на недесятичной системе, очень важны и интересны. Возможно, он вообще был первым учёным, который столь чётко и определённо сформулировал их. Невозможно также не обратить внимания на тональность письма, отличающегося какой-то трогательной, наивной незащищенностью. Оно много говорит о времени, когда социальное происхождение человека – вне зависимости от его текущего социального статуса, было столь важным. Но ощущается в нём и обостренное чувство собственного достоинства автора – особенно в словах о том, что ему важны не похвалы и приятные слова, а беспристрастная научная экспертиза. В то же время, письмо не оставляет сомнений в том, что, наученный печальным опытом, Фаулер совершенно не желает передавать детали своего изобретения в чужие руки. По той же причине он отклонил предложение Айри напечатать описание своей машины.

В сентябре 1840 г. Дж. Айри напечатал заметку о машине Фаулера в Трудах секций Британской ассоциации [32] (она является кратким пересказом сообщения де Моргана и дополнительной информации о конструкции машины не содержит). Вообще Айри по достоинству оценил работу изобретателя-самоучки. Именно Айри представлял изобретение Фаулера на собрании Британской ассоциации осенью 1841 г.: “М-р Айри дал отчёт о новой вычислительной машине м-ра Фаулера. Машина была задумана с целью облегчить попечителям округа в Девоншире вычисление пропорций, в которых должны быть распределены налоги между несколькими приходами. Главной особенностью машины является то, что вместо общепринятого десятичного представления чисел используется троичная запись; вес цифр, записываемых слева, увеличивается не десятикратно, но втрое; таким образом, 1 и 2 означают один и два как обычно, но 10 означает не десять, а 3, 11 - четыре, 12 - пять. В то же время 2 может быть представлено как три, уменьшенное на единицу. Теперь пусть единица с чертой сверху означает вычитание; тогда числа 12 и 2 оба означают одно и то же, а именно пять; и по подобной причине, заменяя 2 на 1 , мы получаем несколько способов записи пяти: 12, или 2 , или 1 . Последний способ - форма, принятая в машине. Очевидно, что любое число может быть выражено набором таких положительных или отрицательных единиц. В машине, для представления цифр или 1, когда они требовались в процессе вычислений, были применены рейки” [33]. В целом, констатирует отчёт, машина основана на старом принципе абака или счётных палочек. Интересную информацию добавляет следующее замечание: “На первый взгляд благодаря своим клавишам машина напоминает пианофорте или орган…” [25, с. 10]). Это замечание тем более интересно, что Фаулер не только в течение многих лет был органистом в церкви св. Михаила, но и в своё время пытался стать органным мастером и даже сам их изготавливал.

К сожалению, как писал позднее Хью Фаулер: “Тогдашнее правительство отказалось даже взглянуть на машину моего отца на том основании, что они без удовлетворительного результата потратили столь большие суммы на вычислительную машину Бэббиджа” (цит. по [25, с. 11]). Действительно, по печальному стечению обстоятельств, именно в это время британское правительство рассматривало вопрос об окончательном прекращении финансирования разработки разностной машины Чарльза Бэббиджа (соответствующее решение было сообщено Бэббиджу 4 ноября 1842 г.). Вести в этот момент речь о выделении средств на новый проект, было, разумеется, совершенно невозможно.

Однако дело было не только в отсутствии финансирования со стороны правительства или в стеснённых материальных обстоятельствах самого Фаулера. Со временем Фаулер всё яснее начал осознавать, что машина имеет серьёзные конструктивные недоработки. В первую очередь надо указать на отсутствие механизма автоматического переноса (который, впрочем, был самым проблематичным узлом механических сумматоров и арифмометров ещё длительное время после Фаулера). В описании де Моргана о нём говорится крайне скупо – понятно лишь, что механизм был съёмным (“в настоящее время отсоединён … но легко может быть прикреплен к механизму множителя или делителя и работать совместно с ними”). Так как во время выполнения операции перенос не производится, её результат мог содержать не только цифры 0, 1 и , но также и 2, , 3 и (что означает сдвиг реек блока произведения на соответствующее число позиций). Согласно описанию де Моргана, механизм переноса управлялся вручную, и применялся после выполнения умножения последовательно ко всем парам соседних разрядов результата: “Одним движением руки он [механизм переноса] сдвигает левую рейку на позицию вперед, а правую – на три позиции назад” [15]. Хотя, по мнению де Моргана, для безошибочной работы требуется “лишь небольшой навык”, выполнение каждой операции умножения или деления всё-таки неизбежно превращалось – особенно при операциях с большими числами (разрядность троичной машины Фаулера составляла 55 тритов) – в длительную и чреватую ошибками процедуру.

Возможно, Фаулер и сумел бы решить эту проблему. Однако была ещё одна, не менее важная: необходимость использования вспомогательных таблиц для перевода исходных данных из десятичной системы в уравновешенную троичную и перевода полученных результатов обратно в десятичную систему. Если было необходимо произвести длительные вычисления (например, по какой-либо формуле), то такие накладные расходы были не слишком заметными. Однако если надо было просто перемножать или делить пары чисел, использование машины Фаулера становилось крайне неэффективным.

Скорее всего, именно в этом, в конце концов, Фаулер стал видеть самое серьёзное препятствие на пути к признанию своей машины. Поэтому, когда он вернулся к своей разработке, то решил на этот раз строить уже десятичную вычислительную машину. Работа над ней началась, судя по всему, уже в середине 1841 г. В письме Ф. Бейли от 19 октября он сообщает: “… моя главная цель в настоящее время ограничена обычной десятичной системой, я изготовил деревянную одноразрядную модель, соответствующую этой системе и убедился в её совершенной работе; я, таким образом, убежден, что принципы Машины … могут быть всецело и немедленно приспособлены к десятичной системе… возможно, в течение нескольких месяцев я сумею своими руками изготовить Машину, если милостивый Господь продлит мою жизнь и у меня будет соответствующая возможность… ” (цит. по [25, с. 10-11]).

Как и троичная, новая машина была основана на принципе сдвигающихся реек, только для каждой цифры было добавлено соответствующее число состояний. И хотя базовым числом для вычислений было 10, это снова была уравновешенная система – пятеричная, цифры которой изменяются от ?5 до 5. Таким образом, проблема перевода из обычной десятичной системы при вводе чисел в машину и при считывании результатов так и осталась нерешённой...

Можно предполагать, что и эту машину Фаулер видел только промежуточным этапом своих разработок. В цитировавшемся выше письме Ф. Бейли он заявлял, что тот же принцип может быть распространён на системы счисления с любым основанием, и что пределом здесь служат только возможности механического конструирования. Фаулер писал, что его особо привлекает основание 30 (это число является произведением трёх первых простых чисел: 2?3?5=30) и что он не сомневается в возможности изготовить такую машину разрядностью 40 или 50, а при особо аккуратной работе – даже до 100. Эта “чудесная машина”, всю конструкцию которой он ясно “видит своим мысленным взором”, сможет вести вычисления в любой системе счисления с основанием от 2 до 30. Фаулер полагал, что сумеет продемонстрировать её практичность на модели ещё до начала изготовления рабочего образца.

Постройку своей второй машины Фаулер завершил в 1842 г. Однако 31 марта следующего года изобретатель скончался от “грудной водянки” (гидроторакс), так и не успев ознакомить научную общественность ни со второй машиной, ни с дальнейшими своими планами. В воспоминаниях сына рассказывается, как отец, умирая, продолжал диктовать дочери какие-то соображения по улучшению конструкции…

Вторая машина Фаулера описана в его опубликованной спустя два года после смерти брошюре [21]. В 1844 г. она некоторое время была выставлена в Королевском колледже, по случайному стечению обстоятельств, вместе с разностной машиной Ч. Бэббиджа. Затем она хранилась в совершенно неприспособленном для этого помещении, и вернулась к Хью Фаулеру в ужасающем состоянии, ? некоторые части были утеряны, и восстановить машину не представлялось возможным. Последняя возможность утвердить важность работы Фаулера была потеряна…

* * *

Рис. 7. Витраж

Мы знаем, что троичную вычислительную машину Фаулера наблюдали в действии Чарльз Бэббидж, Август де Морган, Джордж Айри и другие ведущие английские математики и астрономы. Они констатировали как оригинальность конструкции, так и её эффективность. Опубликуй Томас Фаулер свой проект, он, без сомнения, получил бы поддержку и других учёных. К сожалению, этого не случилось. Ни рукописи Фаулера, ни сами машины не сохранились. Сегодня мы можем судить о ней только по описанию А. де Моргана и немногочисленным замечаниям, разбросанным в письмах Фаулера. Единственным же сохранившимся изображением машины Фаулера является цветной витраж, установленный в 1864 г. Хью Фаулером в память об отце в нефе церкви св. Михаила в Торрингтоне (рис. 7).

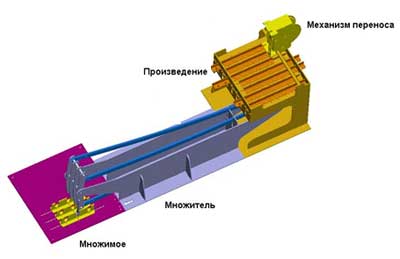
Рис. 8. Чертеж модели

Рис. 9. Марк Глускер с моделью машины Фаулера

Рис. 10. Механизм представления множимого

В августе 2000 г. на основе этих скудных данных исследователь из США Марк Глускер создал работающую модель машины Фаулера [23-25] [21] Разрядность операндов в ней равна трём, таким образом, длина произведения составляет семь тритов (максимально представимое число, следовательно, равняется 1093). На рис. 8 изображена схема построенной им модели, сама модель и её автор показаны на рис. 9. На рис. 10 представлен крупный план механизма представления множимого, а на рис. 11 ? механизмы выработки произведения и переноса (фотографии взяты с сайта http://www.mortati.com/glusker ). К сожалению, очень трудно судить, насколько модель Глускера соответствует оригиналу, поэтому её скорее стоит рассматривать как фантазию на тему “а как можно было бы это сделать”.

Необходимо отдавать отчёт в том, что машину Фаулера вряд ли возможно сравнивать не только с грандиозной по замыслу аналитической машиной, но и с разностной машиной Ч. Бэббиджа (хотя некоторые историки такие попытки и делают). Дело даже не в несопоставимости размеров, некорректно само сопоставление универсальной программно-управляемой вычислительной машины и устройства, предназначенного лишь для умножения чисел, фактически – арифмометра. При этом всё-таки нельзя не признать, что в одном отношении машина Фаулера действительно превосходила машины Бэббиджа – речь идет об использовании уравновешенной троичной системы счисления. Но, между прочим, это понимал и сам Бэббидж. Известный геолог и палеонтолог Уильям Бакленд (1784-1856) в письме Айри от 20 мая 1840 г. упомянул, что в разговоре с ним величайшим достоинством машины Фаулера Бэббидж назвал то, что она основана на ином принципе, нежели его собственная машина (цит. по [25, с. 10]). В машинах Бэббиджа, выполнявших вычисления над десятичными числами, требовалась крайне сложная и громоздкая система вращающихся колес, угол поворота которых задавал цифры от 0 до 9. Вместо неё Фаулер применил систему скользящих реек, занимавших одно из всего лишь трёх возможных положений. Она может быть достаточно просто реализована и не требует высокой точности изготовления деталей (именно поэтому Фаулер мог изготовлять их из дерева).

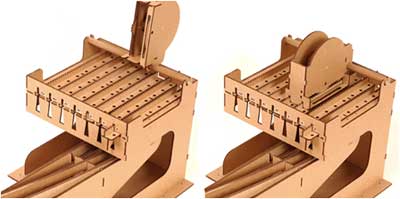
Рис. 11. Механизм переноса и произведение

Сегодня невозможно судить, могло ли изобретение Фаулера серьёзно повлиять на развитие вычислительной техники. Но вовсе не исключено, что, стань работа Фаулера в своё время широко известна, она могла бы направить конструкторскую мысль в новое русло. Ведь ещё многие десятилетия продолжали разрабатываться вычислительные машины, основанные исключительно на десятичной системе. Даже созданная ровно через сто лет электромеханическая машина “Mark I” Говарда Айкена (1900-1973) работала в десятичной системе, что и предопределило её крайнюю сложность и громоздкость. Во всяком случае, попытки использовать недесятичные системы счисления в механических или электромеханических вычислительных машинах могли бы случиться задолго до двоичных машин, предложенных в 1932 г. французом Раймоном Вальта и в 1936 г. англичанином Уильямом Филлипсом (1892-1968) и немцем Конрадом Цузе (1910-1995).

Впрочем, как ни банально это звучит, история действительно не знает сослагательного наклонения. Работа Фаулера была забыта ровно на полтора века. Его имя вышло из забвения только в 1993 г., когда известный историк техники Дорон Суэйд, автор нескольких книг о Чарльзе Бэббидже и руководитель успешного проекта реконструкции его разностной машины, обнаружил в архиве переписку Фаулера и Айри [37]. По словам Хью Фаулера, отец верил, что именно эта машина принесет ему славу – что же, в этом изобретатель оказался прав, пусть слава и пришла к нему с таким опозданием.

Публикации о Фаулере и его машинах не слишком многочисленны: помимо публикации Д. Суэйда, большой интерес представляют работы [39, 25] (её авторы Памела Васс и Девон Хоган играют ключевую роль в популяризации имени и наследия Фаулера), а также уже упомянутые публикации М. Глускера о реконструкции машины [23, 24] и заметка П. Кристи [12]. На русском языке, кроме маленькой заметки Л. Черняка [5], о ней были опубликованы две статьи [6, 7] (настоящая работа является их исправленным и значительно расширенным вариантом).

Замечание. Несколько отвлекаясь от темы, хочется сказать, что имя королевского астронома Джорджа Бидделла Айри не раз встречается на страницах истории вычислительной техники, - причём его роль в ней весьма неоднозначна. В частности, широко известен его длившийся несколько десятилетий конфликт с Ч. Бэббиджем; Айри приложил немало усилий для того, чтобы правительство отвергло не только проект разностной машины Бэббиджа, но и некоторые другие его предложения (Айри фактически был научным советником британского кабинета, и судьба многих значимых проектов зависела от его мнения). С другой стороны, Айри прекрасно понимал всю практическую важность проблемы вычислений и необходимость создания средств их механизации (например, в одной малоизвестной публикации 1856 г. он высоко оценил разностную машину Шютцев и призвал строить подобные устройства). Участие, проявленное к Фаулеру, могло быть следствием этого понимания. И ещё один интересный факт. В математике известен так называемый интеграл Айри, являющийся решением дифференциального уравнения второго порядка y''=xy. Именно вычисление таблицы значений этого интеграла было выбрано Морисом Уилксом в качестве первой серьёзной задачи для решения на компьютере EDSAC , первом в мире компьютере с хранимой в памяти программой. Соответствующая программа (июнь 1949 г.) стала первой в истории, написанной для компьютеров с фон-неймановской архитектурой, которую её авторам пришлось отлаживать (написанные до этого небольшие тесты были очень простыми и ошибок не содержали). Эта же программа, состоявшая всего из 126 команд, содержала около 20 ошибок! С их обнаружения и исправления берёт начало теория и практика отладки программ (подробности можно найти в интересной работе [10]). Кстати, сам Уилкс считает Айри одним из наиболее выдающихся вычислителей в истории (в одном из писем он даже назвал его “своим героем”).

Примечания

1. Тит Ливий Буратини (1617-1681) – итальянский архитектор и изобретатель, почти всю свою жизнь работал в Польше.

2. Сэмюэл Морленд (1625-1695) – английский инженер и изобретатель.

3. Томас Гарриот (1560-1621) – выдающийся английский ученый, математик, астроном и оптик.

4. Нельзя не отметить также, что в Древнем Египте использовался метод умножения, основанный на последовательных удвоениях и сложениях. В его основе фактически лежит неявное двоичное представление чисел. Однако двоичная система счисления египтянам, конечно, ещё не была известна.

5. Колсон также обещал в ближайшее время довести до сведения “всех интересующихся” описание изобретенного им счетного инструмента – абака или счетной доски, с помощью которого, по его утверждению, можно существенно облегчить самые сложные вычисления в любой системе счисления, использующей его “положительно-отрицательную арифметику”.

6. Клод Гаспар Баше де Мизирьяк (1581-1638) – французский математик.

7. Подробный исторический обзор и детальный анализ развития недесятичных систем счисления можно найти в монографии А. Глезера [22]. Отметим только, что работа Колсона, судя по всему, была основательно забыта, поскольку Глезер о ней не упоминает.

8. Грош полагал, что для изготовления сердечников можно будет использовать один из видов магнитного никель-железного сплава (пермаллоя). Об уравновешенной троичной системе Грош узнал на вечерних курсах для сотрудников IBM . Интересно, что на этих курсах троичные разряды называли не тритами, а титами ( tits ), что служило постоянным источником для шуток слушателей (жаргонное слово tits означает женский бюст)…

9. Британским законодательством того времени детский труд не регламентировался – первый закон, ограничивавший рабочий день детей от 9 (!) до 13 лет на текстильных фабриках восемью часами, был принят лишь в 1833 г.

10. Без сомнения, это можно считать большой удачей, поскольку до 1834 г. английское правительство вообще не финансировало (крайне немногочисленные) школы, которые содержались исключительно на средства частных лиц и различных обществ. Обязательным начальное образование стало в Англии только в 1870 г.

11. Имеется в виду книга профессора Николаса Сондерсона (1682-1739) “The Method of fluxions…”, подготовленная к печати и впервые изданная в 1756 г. его сыном. Она представляла собой адаптированное изложение знаменитого труда И. Ньютона “Principia Mathematica”.

12. Цит . по : The Thomas Fowler story by John McKay [ http://www.thomasfowler.org.uk/ ].

13. Термосифон Фаулера иногда не слишком критично называют первым прообразом современных систем центрального водяного отопления. На самом деле первая такая система была построена ещё в 1777 и описана в 1782 г. в адресованном Академии наук докладе французского инженера и изобретателя Жана Симона Боннемана (1743-1830). Первоначально Боннеман применял её для обогревания инкубаторов и выращивания цыплят, позднее – для обогревания оранжерей и жилых помещений. Работавший в Англии французский эмигрант маркиз Жан-Фредерик де Шабанн (1762-1836) опубликовал в Лондоне в 1815 и 1818 гг. две брошюры с описанием своей системы водяного отопления жилых и общественных зданий. Кроме того, известно множество работ других изобретателей, в 1810-х – 1830-х гг. выдвигавших предложения по совершенствованию систем водяного отопления.

14. См. Gardener ? s Magazine (vol. V, 1829, с . 453; vol. VI, 1830, с . 377; vol. VII, 1831, с . 612 и др .).

15. См.: An Encyclop?dia of Gardening . London , 1835. Pp . 600-601.

16. Позднее Фаулер понял, что машину можно применять для решения и других задач. Так, в одном из писем он говорит, что “нашел её полезной для всех, даже самых обширных, вычислений государственных фондов, комиссионных выплат, составления таблиц с точностью до миллионных долей фартинга…” (цит. по [25, с. 4]). В другом ? что его машину можно по праву назвать Логарифмической, поскольку он с успехом вычислял на ней логарифмы с очень большой точностью (до 70 и 80 десятичных знаков), причём делать это можно разными методами [25, с. 10]. Последнее замечание скорее всего означает, что Фаулер хорошо осознавал преимущество своей (универсальной) машины над специализированной разностной машиной Бэббиджа.

17. Фрэнсис Бофорт ( 1774-1857 ) – британский адмирал, в 1805 г. предложил двенадцатибалльную шкалу оценки силы ветра.

18. Уильям Бейли (1774-1844) – английский астроном.

19. Британская ассоциация за прогресс науки, созданная в 1831 г.

20. Цит . по : The Thomas Fowler story by John McKay [ http://www.thomasfowler.org.uk/ ].

21. Впоследствии автор передал эту модель в музей Большого Торрингтона.

Литература

1. Брусенцов Н. П. Из истории создания троичных цифровых машин в МГУ // Историко-математические исследования. Вторая серия. Вып. 10 (45). М.: Янус-К, 2005. С. 28-53.
2. Гутер Р. С., Полунов Ю. Л. Двоичная арифметика в инструментальном счете у Джона Непера // Историко-математические исследования. Вып. 23. М.: Наука, 1978. С. 156-167.
3. Кнут Д. Искусство программирования для ЭВМ. Т. 2. Получисленные алгоритмы, пер. с англ. М.: Мир, 1977. 724 с.
4. Стройк Д. Я. Краткий очерк истории математики. Изд. второе, пер. с нем. М.: Наука, 1969. 328 с.
5. Черняк Л. Троичная машина в XIX в. // Computerworld Россия. 12 ноября 2002. № 42. С. 31.
6. Шилов В.В. К истории троичных вычислений // Компьютеры в учебном процессе. 2004. № 2. С. 3-14.
7. Шилов В.В. Три эпизода из истории вычислительной техники // Информационные технологии. 2005. № 10. С. 65-79.
8. Barlow P. An Elementary Investigation of the Theory of Numbers. London, 1811. 507 p.
9. Bernan W. On the History and Art of Warming and Ventilating Rooms and Buildings. Vol. II. L.: George Bell, 1854. 335 p.
10. Campbell-Kelly M. The Airy Tape: An Early Chapter in the History of Debugging // Annals of the History of Computing. 1992. Vol. 14. № 4. Pp. 16-26.
11. Cauchy A. Sur les moyens d¢éviter les erreurs dans les calculs numériques//Comptes rendus hebdomadaires des séances de l¢Académie des sciences. 1840. F. 11. Pp. 789-798, 826.
12. Christie P. Wooden Computer Invented in North Devon // in: North Devon History.P. Christie, ed., Edward Gaskell, 1995. Pp. 29-30.
13. Colson, John. A short account of negativo-affirmative arithmetick // Philosophical Transactions of the Royal Society of London. 1726. Vol. 34. Pp. 161-173.
14. Croarken M. Tabulating the Heavens: Computing the Nautic Almanac in 18th-Century England // Annals of the History of Computing. 2003. Vol. 25. № 3. Pp. 48-61.
15. De Morgan, Augustus. Description of a calculating machine, invented by Mr Thomas Fowler of Torrington in Devonshire. Archive Papers. Vol 23. № 24. The Royal Society, London. June 1840. [http://www.mortati.com/glusker/fowler/demorgan.htm].
16. De Morgan, Augustus. Description of a Calculating Machine Invented by Mr. Thomas Fowler, of Torrington in Devonshire // Abstracts of the Papers Printed in the Philosophical Transactions of the Royal Society of London, 4 (1837-1843). Pp. 243-244.
17. Eels W. C. Number Systems of North American Indians // American Mathematical Monthly. 1913. Vol. 20. P. 293.
18. Fowler, Hugh. Biographical Notice of the late Mr Thomas Fowler of Torrington with some account of his inventions // Report in the Trans. Devon Assoc. Advancement of Science. 1875. Vol. 7. Pp. 171-178.
19. Fowler, Thomas. A Description of the Patent Thermosiphon with Some Modes of Applying it to Horticultural and Other Useful and Important Purposes. London: Longman, Orme, Brown, Green and Longmans, 1829. 40 p.
20. Fowler, Thomas. Tables for Facilitating Arithmetical Calculations. London: Longman, Orme, Brown, Green and Longmans, 1838. 56 p.
21. Fowler T. Description of the table part of the New Calculating Machine invented by Thomas Fowler of Great Torrington, Devon in 1842, pamphlet, printed by M. Fowler, Great Torrington, Devon, England, 1844, and compiled in “Mathematical Tracts 1848”, A. De Morgan, ed., Ref. L (bound pamphlet 39) item 26, Senate House, Univ. of London Library.
22. Glaser A. History of Binary and Other Nondecimal Numeration. Los Angeles, CA: Tomash Publishers, 1981. 218 p.
23. Glusker M. Thomas Fowler¢s Ternary Calculating Machine //The British Society for the History of Mathematics.Summer 2002. Vol. 46. Pp. 2-5.
24. Glusker M. Thomas Fowler¢s Ternary Calculating Machine: How a 19th Century Inventor¢s Departure from Decimal Presaged the Modern Binary Computer // Journal of the Oughtred Society. Fall 2002. Vol. 11. № 2. Pp. 48-49.
25. Glusker M., Hogan D. M., Vass P. The Ternary Calculating Machine of Thomas Fowler // Annals of the History of Computing. 2005. Vol. 27. № 3. Pp. 4-22.
26. Grosch, Herbert R. J. Computer: Bit Slices From a Life. Novato, CA: Third Millennium Books, 1991.
27. High Speed Computing Devices. Engineering Research Associates. N.-Y.: McGraw Hill, 1950. Pp. 287-289.
28. Hood, Charles. A Practical Treatise on Warning Buildings by Hot Water… 3rd ed. London: Whittaker and Co, 1855. P. 142.
29. Lalanne, Léon. Note sur quelques propositions d¢arithmologie élémentaire // Comptes rendus hebdomadaires des séances de l¢Académie des sciences. 1840. F. 11. Pp. 903-905.
30. Leibniz G. W. Explication de l¢arithmétique binaire // Memoires de l¢Académie Royale des Sciences. 3. 1703. Pp. 85-89.
31. Mr. Fowler of Devonshire¢s Mode of Heating by Hot Water // The Gardener¢s Magazine. 1831. Vol. VII. Pp. 376-378.
32. Notice of Mr Fowler¢s new Calculating Machine, Communicated by Professor Airy // Transactions of Sections. Vol. 10. British Assoc. for the Advancement of Science, Sept. 1840. P. 55.
33. On a New Calculating Machine by Mr. Fowler // Transactions of Sections. Vol. 11. British Assoc. for the Advancement of Science, Sept. 1841. Pp. 39-40.
34. Shannon C. E. A symmetrical notation for numbers // American Mathematical Monthly. 1950. Vol. 57. № 2. Pp. 90-93.
35. Shirley J. W. Binary numeration before Leibniz // American Journal of Physics. 1951. Vol. 19. Pp. 452-454.
36. Specification of the Patent granted to Thomas Fowler, of Great Torrington, Devonshire, for certain Improvements in, or for raising and circulating hot Water, hot Oils, and other hot Fluids, for domestic and other purposes. – Dated October 20th, 1828 // The Repertory of the Patent Inventions… Vol. IX. London, 1830. Pp. 393-419.
37. Swade D. “It will not slice a pineapple”: Babbage, Miracles and Machines // in: F. Spufford and J. Uglow (eds). Cultural Babbage: Technology, Time and Invention. London: Faber and Faber, 1996.
38. To Thomas Fowler, of Great Torrington, in the county of Devon, stationer, for his invention of certain improvements in or for raising and circulating hot water, hot oils, and other hot fluids, for domestic and other purposes. – [Sealed October 2, 1828] // The London Journal of Arts and Sciences. Second Series. Vol. 9. London, 1834. Pp. 82-85.\
39. Vass P. Rediscovering Thomas Fowler (1777-1843): Mathematician and Inventor //Report and Transactions of the Devonshire Association for the Advancement of Science. December 1999. Vol. 131. Pp. 11-25.

Статья помещена в музей 11.05.2009.