Вычислительные машины и устройства на вероятностном принципе

Б. Ф. Кирьянов, В. М. Кузнецов, В. А. Песошин

1. Введение

Работы Гейнса Б.Р. [1], Poppelbaum W.J. [2] и Ribeiro S.T. [3] положили начало развитию класса стохастических вычислительных машин (СВМ), основные арифметические блоки которых реализуются на цифровой элементной базе. При этом алгоритм решения задач, как в аналоговых вычислительных (АВМ), так и в цифровых интегрирующих машинах (ЦИМ), определяется способом соединения элементов, выполняющих математические операции, а реальные переменные величины в общем случае линейно связаны с машинными переменными в форме вероятностей появления случайных символов 1 или 0 в дискретные моменты времени t. Такой выбор машинных величин и, как следствие, стохастический (вероятностный) принцип реализации операций, связанный с абстрагированием от конкретных последовательностей символов, вносит специфику как в способы построения устройств СВМ, так и в методы их исследования.

2. Блок – схема СВМ

В общем случае блок-схема СВМ предполагает включение устройств, представленных на рисунке.

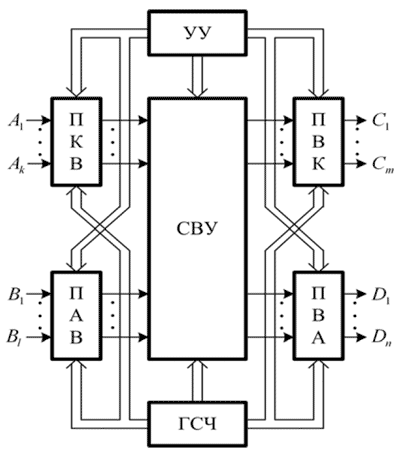
Блок-схема СВМ

• устройства ввода информации, служащие для преобразования дискретной и аналоговой информации в последовательности случайных символов, в которых вероятность появления символа 1 пропорциональна величинам входных сигналов (преобразователи кодвероятность (ПКВ) и аналог-вероятность (ПАВ) соответственно);
• стохастические вычислительные устройства (СВУ), которые обеспечивают выполнение различных операций на вероятностном принципе;
• устройства вывода информации, преобразовывающие результирующие вероятности случайных двоичных символов в цифровую или аналоговую форму (преобразователи вероятность-код (ПВК) и вероятностьаналог (ПВА) соответственно);
• генераторы случайных и псевдослучайных чисел (ГСЧ и ГПСЧ), служащие для формирования стохастических констант и случайных сигналов (как правило, с равновероятным законом распределения), необходимых для функционирования устройств ввода и вывода информации;
• устройство управления, обеспечивающее, как и в любой вычислительной машине, координацию работы всех устройств во времени с целью осуществлениям заданного алгоритма вычислений.

3. Выполнение операций на стохастическом принципе и основные устройства СВМ

В CBM реальные величины Х, не превышающие X_max , представляются машинными переменными в форме вероятностей p_x = P{x = 1}, которые естественно предполагают непрерывный интервал изменения (0, 1). При этом случайная величина х дискретна и принимает лишь два значения 0 и 1, характерные для переключательных функций логических элементов СВУ. Физически двоичные переменные х представимы случайными последовательностями x(t) . Описанные условия в простейшем однополярном случае обеспечиваются следующим выражением: p_x = X / X_max, где 1/X_max– масштаб представления реальной положительной величины Х машинной переменной p_x

Аналогичные масштабные соотношения применяются для АВМ, ЦИМ и ЭВМ с фиксированной запятой.

Опишем несколько характерных примеров выполнения арифметических операций на стохастическом принципе.

Умножение двух величин. Если x₁ и x₂ – символы входных случайных последовательностей конъюнктора (элемента И), а у – символы его выходной последовательности, т.е. y=x₁x₂, то выражение p_y = p_x1p_x2 + K_x1x2(0) демонстрирует операцию умножения вероятностей. При этом K_x1x2(0) – взаимная корреляционная функция при отсутствии временного сдвига воспринимается как погрешность выполняемой операции. Обеспечивая техническими средствами СВМ отсутствие корреляции в виде K_x1x2(0) = 0, получаем идеальную реализацию стохастического умножения в форме p_y = p_x1p_x2.

Аналогично организуется умножение более чем двух вероятностных переменных на многовходовом конъюнкторе при условии попарно взаимной некоррелированности всех входных последовательностей.

Сложение. Подобное рассмотрение двухвходового дизъюнктора (элемента ИЛИ) сопровождается записью y = x₁ ∨ x₂, что в вероятностной трактовке соответствует функции p_y = p_x1 + p_x2 – p_x1x2. Полученное соотношение представляет операцию сложения вероятностей, для которой компонент – p_x1x2 является погрешностью. Для устранения этой погрешности вводятся два дополнительных потока несовместных равновероятных двоичных символов. В результате получаем реализацию операции стохастического сложения в форме p_y = 0,5 (p_x1 + p_x2), содержащей необходимый для вероятностного представления суммы двух вероятностей масштабный коэффициент 0,5.

Дополнение до единицы. Эта операция реализуется с помощью инвертора, для которого p_y = 1 – p_x.

Возведение в степень. Для организации операции возведения в целую положительную степень n необходимо подать на n-входовый конъюнктор последовательность x(t) и ее сдвинутые регистром копии x(t-1) , x(t-2) ,…, x(t-n+1) . Вероятностное описание выхода конъюнктора представится в виде следующей операции стохастического возведения в степень p_y = p_xⁿ, предварительно обеспечив условие отсутствия автокоррелированности исходной последовательности x(t) в форме K_xx(1) = K_xx(2) = … =K_xx(n-1).

Генераторы случайных чисел. Задание исходных вероятностных переменных для реализации стохастических операций происходит на основе множества некоррелированных равновероятностных двоичных последовательностей, формируемых с помощью ГСЧ и (или) ГПСЧ. Создание высококачественных, быстродействующих и достаточно простых ГСЧ является одной из основных проблем, возникающих при реализации стохастического принципа вычислений [4–7]. Часть этих последовательностей используется в работе преобразователей устройств ввода-вывода.

Преобразователи код-вероятность. Для преобразования входных двоичных кодов, сформированных на основе позиционной системы счисления, в вероятность символа 1 случайных последовательностей используются цифровые компараторы. Очевидно, что результатом сравнения кода Х со случайными числами, имеющими равновероятный закон распределения в интервале (0, 1), будет формирование случайной последовательности x(t) с вероятностью p_x = X. Такой же линейный характер преобразования обеспечивают ПКВ на основе стохастического суммирования с масштабными коэффициентами, равными весам двоичных разрядов Х.

Преобразователи аналог-вероятность. Существует ряд методов построения ПАВ. Один из них предполагает аналого-цифровое преобразование входного сигнала с последующим преобразованием кода в вероятность. Возможно также построение преобразователя по типу ПКВ на основе аналогового компаратора и цифроаналогового преобразования равновероятных чисел с ГСЧ. Существенной простотой построения отличаются ПАВ на основе схем с отрицательной обратной связью через аналоговый интегратор.

Стохастические интеграторы. Интегрирование машинной величины в форме функции p_x(t) заключается в формировании машинной величины p_y(t), пропорциональной текущему значению интеграла от p_x(t) по времени t. Принцип работы стохастического интегратора (СИ) по существу аналогичен интегратору ЦИМ. Отличие состоит в случайности входных сигналов приращений x(t) и преобразовании содержимого счетчика интегратора Y в вероятность выходной случайной последовательности y(t) с помощью ПКВ.

Необходимо отметить, что СИ с обратной связью позволяют реализовать ряд арифметических операций на стохастическом принципе по методу обратных функций. Это, например, вычитание, деление, извлечение корня.

Преобразователи вероятность-код. Эти преобразователи по своей основе и функционированию могут использовать время-импульсный метод измерения частоты сигнала посредством интегрирования за фиксированный интервал времени. В случае представления в СВМ знакопеременных величин в качестве ПВК используют следящий режим работы стохастического интегратора с обратной связью.

Преобразователи вероятность–аналог строятся в основном как пассивные или активные фильтры нижних частот на элементах аналоговой техники. Основным уравнением работы ПВА в простейшем случае является X = m_xp_x, где Х – выходное напряжение (аналог), m_X– масштабный коэффициент.

4. История развития исследований по стохастическим вычислительным машинам

В СССР стохастическим машинам большое внимание было уделено работами двух научных школ: под руководством Яковлева Валентина Васильевича в Ленинградском институте инженеров железнодорожного транспорта им. академика В.Н. Образцова (ЛИИЖТ) и Кирьянова Бориса Федоровича в Казанском авиационном институте (КАИ).

Б.Ф. Кирьянов

В.В. Яковлев

В 1970 г. Яковлев В.В и Федоров Р.Ф. выступили с докладом «Возможности использования туннельных диодов в стохастических вычислительных машинах» и это можно считать исходной точкой истории стохастических машин в ЛИИЖТе. Яковлев В.В и Федоров Р.Ф. в 1974 г. издали монографию «Стохастические вычислительные машины» [8]. В 1975 г. Яковлев защитил докторскую диссертацию на тему «Синхронные случайноимпульсные вычислительные устройства с цифровыми решающими элементами». Федоров Р.Ф., Яковлев В.В и Добрис Г.В. в 1978 г. издали монографию «Стохастические преобразователи информации» [9]. В рамках школы по стохастическим методам и средствам вычислений в ЛИИЖТе защищены около 20 кандидатских диссертаций, в том числе выпускниками кафедры ЭВМ Х.Г. Накке и И. Рааш из Германии, П. Кавалец и Г. Пех из Польши, а также:

1973 г. Добрис Г.В. «Исследование принципов построения преобразователей код-вероятность для стохастических вычислительных машин»,

1983 г. Мальченкова О.С. «Исследование стохастических вычислительных устройств с коллективным использованием генераторов случайных и чисел».

В 1990 г. защищена докторская диссертация Пех Г. «Теория построения стохастических устройств для реализации методов статистических испытаний».

С 1969 г. в Казанском авиационном институте на кафедре ЭВМ под руководством доцента Кирьянова Б.Ф. начались работы по госбюджетной научно-исследовательской работе «Построение вычислительных устройств на вероятностном принципе». В 1973 г. по теме «Аппаратурные методы вычислений на основе стохастического принципа» Б.Ф. Кирьянов защитил докторскую диссертацию. В 1974 г. была изготовлена малая стохастическая модель для исследования и отработки принципов стохастических вычислений и вероятностного моделирования. К 1976 г. ими были разработаны теоретические основы построения и функционирования вычислительных устройств на вероятностном принципе – (СВМ). Носителем информации в СВМ является вероятность появления случайных двоичных символов 0 и 1. Разработаны методы построения узлов этих машин, исследованы вопросы точности, эквивалентности, устойчивости и быстродействия, разработаны и исследованы принципы построения вероятностных преобразователей и генераторов случайных и псевдослучайных последовательностей. Результаты работы вошли в монографию Б.Ф. Кирьянова «Основы теории стохастических вычислительных машин и устройств», изданную в Казани в 1975 г., депонированную в ЦНИИТЭИ приборостроения, 1976 г., деп. №524 [10].

С 1976 г. на кафедре ЭВМ КАИ ведутся работы по разработке блока статистического моделирования (БСМ), предназначенного для формирования и ввода случайных и псевдослучайных чисел в ЭВМ. БСМ позволял сгенерировать случайные и псевдослучайные числа с равномерным, нормальным, экспоненциальным, а также с произвольным (задаваемым пользователем, таблицей или гистограммой) законами распределения. Работа основана на использовании аппаратурной реализации генерирования случайных чисел, по которой получены авторские свидетельства СССР. Был изготовлен макет устройства, который экспонировался в 1981 г. на ВДНХ СССР и удостоен бронзовой медали ВДНХ.

Технико-экономические исследования показали целесообразность опытно-конструкторской работы, которая была проведена в СКБ Казанского завода ЭВМ. Заводской вариант БСМ получил название «Устройство ввода случайных чисел» (УВСЧ) и ему присвоен шифр ЕС 6903. Техническое задание на разработку подписано Генеральным конструктором ЕС ЭВМ В.В. Пржиялковским. На заводе ЭВМ были изготовлены 2 опытных образца ЕС 6903. В 1982 г. успешно завершены Государственные испытания ЕС-6903 (председатель комиссии д.ф.-м.н., профессор С.М. Ермаков). В 1983 г. на заводе ЭВМ УВСЧ ЕС-6903 внедрено в серийное производство.

В 1985 году по итогам конкурса на лучшие НИР работе «Устройство для статистического моделирования ЕС 6903» впервые в истории КАИ присуждена II премия Минвуза СССР. В 1988 году за разработку и теоретическое обоснование методов формирования случайных и псевдослучайных чисел для ЭВМ В.А. Песошину присужден диплом почета ВДНХ СССР. В 1985 г. разработано частное техническое задание на опытноконструкторскую разработку ГСЧ для Терминальной ЭВМ ЕС 1007, подписанное Главным конструктором А.У. Ярмухаметовым. Разработаны ГСЧ для бортовой ЭВМ для НИИ ЭВМ (г. Минск), для персональных ЭВМ, большая интегральная схема «Генератор равновероятной случайной последовательности» совместно с Казанским научно-исследовательским институтом радиоэлектроники, в том числе на ПЛИС фирмы Xilinx.

Фотография микросхемы БИС ГСЧ на БМК серии 1537ХМ2

По данному направлению защищены следующие кандидатские диссертации:

1972 г. Глова В.И. Вопросы анализа и синтеза стохастических интеграторов и преобразователей.

1974 г. Скребнев А.А. Вопросы анализа и синтеза линейных преобразователей вероятностных потоков двоичных символов.

1975 г. Песошин В.А. Разработка и исследование методов преобразования аналоговых величин в стохастические потоки двоичных символов.

1977 г. Бондаренко Б.П. Анализ и синтез генераторов последовательностей импульсов со случайными временными интервалами.

1978 г. Тарасов В.М. Разработка и исследование устройств вывода информации из стохастических вычислительных машин.

1979 г. Живетина Т.М. К теории построения функциональных преобразователей многих переменных на основе метода задающих булевых функций.

1979 г. Мансуров Р.М. Разработка и исследование комбинированных генераторов случайных чисел с равномерным законом распределения.

1986 г. Кузнецов В.М. Цифровые устройства формирования случайных сигналов с неавтономным источником шума.

1987 г. Дапин О.И. Генераторы псевдослучайных последовательностей на основе многоуровневых регистровых структур.

1991 г. Сергеев Н.Н. Цифровые полисинхронные генераторы случайных и псевдослучайных чисел.

1992 г. Бурнашев М.И. Генераторы случайных и псевдослучайных чисел на микропрограммируемых БИС.

1997 г. Яхина З.Т. Методы и алгоритмы подготовки и обработки информации для систем статистического моделирования.

1998 г. Гришкин С.Г. Генераторы случайных и псевдослучайных чисел для статистического моделирования и защиты информации.

2006 г. Гришкин А.С. Генераторы псевдослучайных символов на регистрах сдвига с внутренними сумматорами по модулю два при использовании инверсных выходов.

Б.Ф. Кирьянов с учениками: В.М. Кузнецов, В.И. Глова, В.М. Тарасов, В.А. Песошин

По данному направлению защищены следующие докторские диссертации:

1987 г. Песошин В.А. Устройства вычислительной техники для генерирования случайных и псевдослучайных последовательностей и чисел.

1995 г. Глова В.И. Вычислительные средства для статистического моделирования.

1995 г. Захаров В.М. Аппаратно-программная организация специализированных процессоров на основе автономных вероятностных автоматов.

2011 г. Кузнецов В.М. Генераторы случайных и псевдослучайных последовательностей на цифровых элементах задержки (основы теории и методы построения).

5. Заключение

Рассмотренные в статье примеры реализации математических операций на стохастическом принципе в целях иллюстративности предполагают простейшее вероятностное кодирование однополярных величин. Тем не менее, имеются подробные разработки стохастических устройств, основанных на представлении знакопеременных величин.

Необходимо заметить, что в целом СВМ можно классифицировать как ЭВМ, работающую на унитарных кодах. По этой причине возникает существенная избыточность кодирования, которая, с одной стороны, определяет исключительную надежность функционирования аппаратуры. Однако, с другой стороны, заметно снижает быстродействие. Погрешность стохастических вычислений обратно пропорциональна √N , где N – длина выборки последовательности у, необходимая для оценки результирующей вероятности p_y*. Эта длина выборки, по существу, определяет длительность стохастической операции.

Анализируя форму представления случайных событий в СВМ, возникает весьма привлекательная идея перевода последовательностного характера работы отдельных операционных устройств в ансамблевый. Возникающая при этом аппаратная избыточность (астрономическая по меркам тридцатилетней давности) становится вполне реально терпимой в рамках современных достижений микроэлектроники и современных технологий БИС. Например, стохастический умножитель будет представлять собой параллельный набор конъюнкторов, на входы которых будут подаваться параллельные случайные унитарные коды вероятностных операндовсомножителей. В такой же форме будет представлен и операнд-результат с выходов этих конъюнкторов. Время выполнения такой операции умножения выразится задержкой одного уровня конъюнкторов, что принципиально недостижимо для известных детерминированных вычислителей. Количество конъюнкторов K в наборе определит погрешность умножения, которая будет обратно пропорциональна √K . Очевидно, реальна и компромиссная постановка идеи параллельно-последовательностной стохастической обработки информации посредством представления случайных унитарных кодов матрицей K × N .

В заключении уместно подчеркнуть полезность применения апробированных в СВМ вероятностных подходов к проблемам процессорных вычислений, основанных, например, на перспективных наноэлектронных и квантовомеханических технологиях. Ренессанс вероятностных вычислений вполне вероятен!

Список литературы

1. Гейнс, Б.Р. Стохастическая вычислительная машина / Б.Р. Гейнс // Электроника, 1967, №14. – С.3–11.
2. Poppelbaum, W.J. What next in computer Technology Technology / W.J. Poppelbaum // Advances in computer. 1968, v.9.
3. Ribeiro, S.T. Random-pulse machines / S.T. Ribeiro // IEEE Trans. Electron. Computers, 1967, №3.
4. Бобнев, М.П. Генерирование случайных сигналов / М.П. Бобнев. – М.: Энергия, 1971. – 240 с.
5. Варакин, Л.Е. Теория сложных сигналов / Л.Е. Варакин. М.: Советское радио, 1970 – 376 с.
6. Кузнецов, В.М. Генераторы случайных и псевдослучайных последовательностей на цифровых элементах задержки: монография / В.М. Кузнецов, В.А. Песошин. – Казань: Изд-во Казан. гос. техн. ун-та, 2013. – 336 с.
7. Песошин, В.А. Генераторы псевдослучайных и случайных чисел на регистрах сдвига / В.А. Песошин, В.М Кузнецов. Генераторы случайных и псевдослучайных последовательностей на цифровых элементах задержки: монография / В.А. Песошин, В.М. Кузнецов. – Казань: Изд-во Казан. гос. техн. ун-та, 2007. – 296 с.
8. Яковлев, В.В. Стохастические вычислительные машины / В.В. Яковлев, Р.Ф. Федоров. – Л.: Машиностроение, 1974. – 344 с.
9. Федоров, Р.Ф. Стохастические преобразователи информации / Р.Ф. Федоров, В.В. Яковлев, В.Г. Добрис. – Л.: Машиностроение, 1978. – 304 с.
10. Кирьянов, Б.Ф. Основы теории стохастических вычислительных машин / Б.Ф. Кирьянов; Казан. авиац. ин-т. – Казань, 1975.– 186 с. – Деп. в ЦНИИТЭИ приборостроения 21.05.76, №524.

Об авторе: Новгородский государственный университет им. Ярослава Мудрого
Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ
Казань, Россия
pesoshin-kai@mail.ru
Материалы международной конференции Sorucom 2014 (13-17 октября 2014)
Помещена в музей с разрешения авторов 4 апреля 2015