Предыстория автоматизации вычислений в докомпьютерную эпоху
В.И. Тихвинский
(Системы счисления, счётные доски и счислитель Куммера)
Нельзя определить, когда человечество стало разбивать счётные единицы на разряды и изобрело систему счисления (СС) [1], что позволило ему оперировать большими числами. СС это метод записи чисел специальными знаками. Число показывает количество подсчитанных единиц. Единица — “всякая вещь или предмет отдельно, по себе взятый; всякая мера, принятая в этом случае для измеренья чего-либо” [2. с. 466]. Разряд числа – такое условное разделение числа на единицы, когда определённое количество единиц разряда образует единицу старшего разряда, а единица разряда состоит из определенного количества единиц младшего разряда. Число состоит из одной и более цифр, цифра это обозначение на письме количества единиц в разряде числа. СС может иметь одно или несколько оснований. Основание СС – это показатель того, во сколько раз единица разряда больше единицы предыдущего разряда. В СС с более чем одним основанием два разряда и более могут играть роль одного. Каждый разряд числа имеет свой вес, вес разряда показатель того, во сколько раз единицы разряда больше или меньше единиц того разряда, с которого начинается счёт. Существуют позиционные системы счисления (ПСС), в которых цифры одинаковы для всех разрядов, а вес разряда определяется по количеству цифр в числе, и непозиционные СС (НСС), в которых цифры не одинаковы для разрядов, причём цифра обозначает не только количество единиц в разряде числа, но и вес разряда. К ПСС относится современный вариант десятичной системы с цифрами 0-9, данная СС не всегда была позиционной. Десятичная СС (ДСС) не является самой древней, но, пожалуй, это единственная древняя СС с одним основанием, к тому же эта система наиболее понятна для современных людей, поэтому мы сначала рассмотрим её. К наиболее древнему варианту десятичной НСС относится египетская СС (ЕСС). В ЕСС для обозначения единиц, десятков, сотен использовались специальные цифровые иероглифы, из которых составлялись цифры соответствующих разрядов [3]. Современна ДСС перешла к европейцам от арабов, которые, в свою очередь, переняли её у индийцев [4]. И индийцы, и арабы используют в повседневной жизни свои цифры ДСС, отличные от европейских.
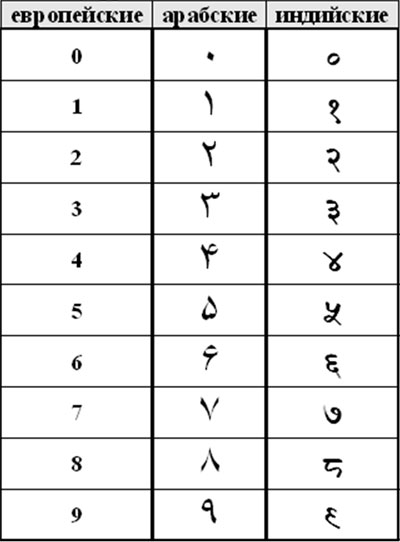
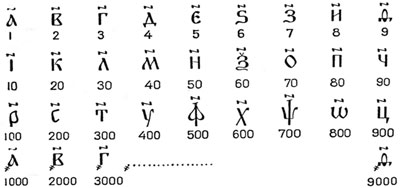
Цифры десятичной ПСС
Древнеегипетские цифровые иероглифы десятичной НСС
|
|
1 |
|
|
10 |
|
|
100 |
|
|
1000 |
|
|
10000 |
|
|
100000 |
|
|
1000000 |
|
|
10000000 |
Примеры записи числа

По-европейски

По-арабски

По-индийски
В поздней десятичной ЕСС цифра, обозначающая несколько единиц или десятков разряда, уже могла не состоять из однотипных повторяющихся элементов [3]. Запись числа стала более простой и компактной.
В ионийской НСС (ИСС), наиболее совершенной десятичной НСС, для обозначения цифр использовались буквы. Подобный принцип для обозначения цифр использовался и славянскими народами [4].
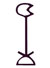
Таким образом, ИСС и основанная на ней славянская СС содержала 27 цифр. Помимо этих цифр имелись и специальные средства для увеличения разрядного веса цифры, например, символы , 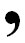 и
и  увеличивали вес цифры в тысячу раз, а если славянская цифра помещалась в круг
увеличивали вес цифры в тысячу раз, а если славянская цифра помещалась в круг  , то вес цифры увеличивался в десять тысяч раз [4].
, то вес цифры увеличивался в десять тысяч раз [4].
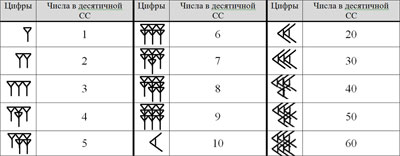
В вавилонской СС (ВСС), самой древней ПСС, единицы и десятки разряда обозначались клином, направленным вниз и вправо [3,4], при этом форма клина не всегда была одинаковой.
В ВСС шестеричный и десятичный разряд могут выполнять функцию одного шестидесятеричного разряда, поэтому она шестидесятеричная СС. Цифры, обозначающие единицы и десятки соседних разрядов, писались слитно.

Нетрудно понять, что внутри шестидесятеричного разряда СС десятичная, поскольку цифра старшего разряда больше цифры младшего разряда в десять раз, а цифра младшего разряда обозначает количество единиц. Возможно, это и породило впоследствии ДСС, и ВСС является родоначальницей ДСС. Так же, как и в ВСС, древнеегипетский цифровой символ сам по себе являлся цифрой, и из повторяющегося символа составлялись другие цифры.
В ВСС первоначально отсутствовала цифра нуль [3, 4], что приводило к неоднозначным чтениям чисел, например, числа 1, 60, 3600 и т.д. записывались одинаково, как клин, направленный вниз  , потому что после цифры
, потому что после цифры  не было цифры нуль или какой-либо другой цифры, изменяющей позицию цифры
не было цифры нуль или какой-либо другой цифры, изменяющей позицию цифры  и повышающей её вес [3].
и повышающей её вес [3].
Неоднозначность чтения чисел сглаживалась поясняющим текстом к задаче, из которого было понятно, о каком числе идет речь, а неоднозначность, вызванная отсутствием нулей между разрядами, сглаживалась большим и малым пробелами между цифрами [3], т.е. число 61 писалось так: 
 , а 3601 писалось так:
, а 3601 писалось так: 
 . Однако для трёх, четырёх и более разрядов определять количество пропущенных разрядов было невозможно. Поэтому для этой цели ввели специальный символ, подобие нашего современного нуля. Судя по [3,4] написание такого символа несколько различалось
. Однако для трёх, четырёх и более разрядов определять количество пропущенных разрядов было невозможно. Поэтому для этой цели ввели специальный символ, подобие нашего современного нуля. Судя по [3,4] написание такого символа несколько различалось 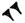 [3],
[3], 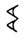 [4]. Т.е. число 3601 можно записать так:
[4]. Т.е. число 3601 можно записать так: 
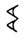
 .
.
Цифра 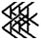 – 60, автором настоящей статьи помещена здесь не случайно. Возможно, и нельзя найти ей историческое подтверждение, но использование этой цифры позволяет не прибегать к вышеуказанным способам (к поясняющему тексту и пробелам) для однозначного чтения чисел ВСС.
– 60, автором настоящей статьи помещена здесь не случайно. Возможно, и нельзя найти ей историческое подтверждение, но использование этой цифры позволяет не прибегать к вышеуказанным способам (к поясняющему тексту и пробелам) для однозначного чтения чисел ВСС.
Т.е. если возникает неоднозначность при чтении разряда шестидесятеричного числа, необходимо вычесть единицу из разряда, а в пустом младшем разряде выразить эту единицу цифрой 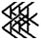 – 60. И теперь уже числа 1, 60, 3600 и т.д. будут читаться однозначно. Единица будет писаться так:
– 60. И теперь уже числа 1, 60, 3600 и т.д. будут читаться однозначно. Единица будет писаться так:
Картинка
. Число 60, чтобы исключить неоднозначность, не будет писаться как единица, а будет писаться так: 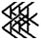 , а число 3600 будет писаться так:
, а число 3600 будет писаться так: 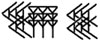 .
.
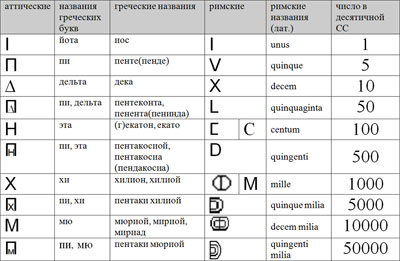
Аттическая СС (АСС) была двоично-пятеричной, в качестве цифр использовались буквы аттического алфавита. Римляне переняли принцип АСС.
Составные цифры двоично-пятеричной СС
|
2 |
Ι Ι |
Ⅰ Ⅰ |
|
3 |
Ι Ι Ι |
Ⅰ Ⅰ Ⅰ |
|
4 |
Ι Ι Ι Ι |
Ⅰ Ⅰ Ⅰ Ⅰ |
|
20 |
Δ Δ |
Ⅹ Ⅹ |
|
30 |
Δ Δ Δ |
Ⅹ Ⅹ Ⅹ |
|
40 |
Δ Δ Δ Δ |
Ⅹ Ⅹ Ⅹ Ⅹ |
|
200 |
Η Η |
Ⅽ Ⅽ |
|
300 |
Η Η Η |
Ⅽ Ⅽ Ⅽ |
|
400 |
Η Η Η Η |
Ⅽ Ⅽ Ⅽ Ⅽ |
|
2000 |
Χ Χ |
Ⅿ Ⅿ |
|
3000 |
Χ Χ Χ |
Ⅿ Ⅿ Ⅿ |
|
4000 |
Χ Χ Χ Χ |
Ⅿ Ⅿ Ⅿ Ⅿ |
|
20000 |
Μ Μ |
ↂ ↂ |
|
30000 |
Μ Μ Μ |
ↂ ↂ ↂ |
|
40000 |
Μ Μ Μ Μ |
ↂ ↂ ↂ ↂ |
Как видно из таблиц, цифра двоичных разрядов составлялась только из одинаковых символов, как и в Древнем Египте десятичные цифры. Согласно [3] в аттическом алфавите первоначально буква 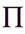 отсутствовала, а буква
отсутствовала, а буква  читалась как “П”. Поэтому цифра пенте (пять) обозначалась буквой
читалась как “П”. Поэтому цифра пенте (пять) обозначалась буквой  , хотя это более чем странно. Согласно [3] греческое слово εκατον(сто) в аттике писалось так: HEKATON, и это не вызывает сомнений.
, хотя это более чем странно. Согласно [3] греческое слово εκατον(сто) в аттике писалось так: HEKATON, и это не вызывает сомнений.
Цифры римской СС (РСС), в отличие от аттических, имели не буквенное, а геометрическое происхождение:
 один
один  линия,
линия,
 пять
пять  острый угол,
острый угол,
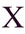 десять
десять  два острых угла,
два острых угла,
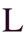 пятьдесят
пятьдесят 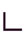 прямой угол,
прямой угол,
 centum, сто логичней изображать как
centum, сто логичней изображать как  два прямых угла,
два прямых угла,
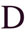 пятьсот
пятьсот 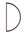 полукруг,
полукруг,
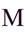 mille, тысяча, в иных вариантах написания
mille, тысяча, в иных вариантах написания  круг, состоящий из двух полукругов,
круг, состоящий из двух полукругов,
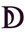 пять тысяч – два полукруга,
пять тысяч – два полукруга,
 десять тысяч – два круга.
десять тысяч – два круга.
Далее количество полукругов и кругов возрастает.
В [4] показаны и иные варианты написания римских цифр, но мы показали наиболее логичные из них.

Варианты написания римских цифр
Как и в ВСС два соседних разряда в РСС могли выполнять функцию одного разряда. Т.е. двоичный и пятеричный разряд в РСС могли выполнять функцию одного десятичного. В этом случае двоичные цифры в РСС обозначают единицы десятичного разряда, а пятеричные пять единиц. Как и в ВСС, в РСС единицы десятичного разряда составлялись из одинаковых, повторяющихся символов. Возможно, ВСС является родоначальницей пятерично-десятичной СС. В РСС числа четыре и девять, сорок и девяносто и т.д. писались так IIII, VIIII, XXXX, LXXXX [4]. Сокращения записи римских цифр IV, IX и т.д. делают невозможными вычисления.
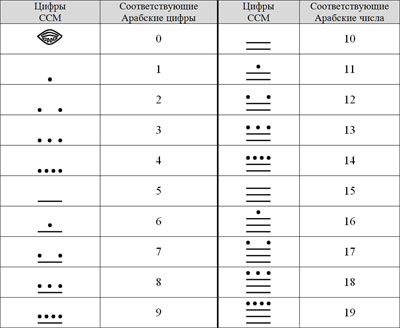
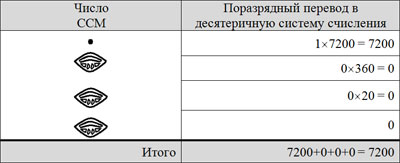
ПСС, использующую цифру нуль, изобрели и в Новом Свете жрецы майя. СС майя (ССМ) была двадцатеричной [5,6].
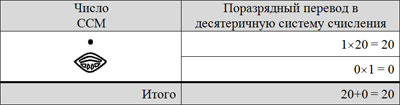
Пример двухразрядного числа
ССМ была СС с двумя основаниями, но порядок СС нарушался для третьего разряда, что было связано с астрономическими вычислениями.
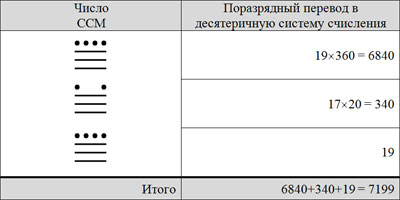
Примеры трёхразрядного и четырёхразрядного числа
Все последующие разряды в ССМ были в 20 раз больше предыдущего.
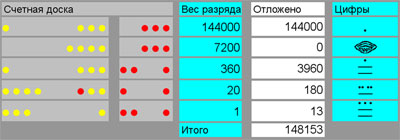
СС была тесно связана со счётной доской (СД). СС позволяла записать результат вычислений на папирусе, бумаге или другом носителе, а СД позволяла хотя бы отчасти автоматизировать вычисления.
Как это не парадоксально может показаться, но ещё до середины XX века при вычислениях активно использовались счёты, которые по своей сути являлись абаком или СД [4]. Неизвестно, кто изобрел СД, но ясно то, что это было гениальным изобретением, которое использовалось на протяжении тысячелетий. Простота и дешевизна этого устройства привели к тому, что счёты активно использовались профессиональными счетоводами для выполнения на них четырёх арифметических операций. СД представляет собой доску, разделённую на полосы (разряды), в которых движутся счётные марки [1,3,4]. Марки откладываются или сбрасываются в определённом направлении. Количество отложенных марок обозначает количество отложенных единиц в разряде числа. Марки старших разрядов имеют больший числовой вес, чем марки младших разрядов. В каждом разряде можно осуществлять счёт поразрядно, добавляя и сбрасывая отложенные марки. Количество марок в разряде определяется системой счисления (СС).

Счётные марки откладываются в левую часть счётной доски, а сбрасываются в правую. Десятая марка предназначена для того, чтобы можно было запомнить перенос единицы в старший разряд, даже если там уже отложено девять марок. Перенос осуществляется в том случае, если сумма добавляемых единиц разряда и сумма отложенных марок младшего разряда превышает 9.
Так называемые современные русские счёты устроены подобным образом, только разделителем между дробными разрядами являются четыре счётные марки, нанизанные на проволоку.
Первоначально на Руси счёты назывались дощаный счёт, причём основание дробных разрядов было не десятичным [7]. В современных счётах такой разряд сохранился в виде проволоки с четырьмя марками. При помощи этих марок можно при необходимости отложить и количество четвертей. Т.е. число 401,25 (или 401 с четвертью) можно отложить следующим образом.
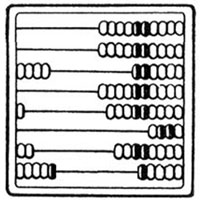
Отложено 401,25
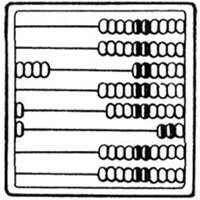
Отложено 401 ¼
Умножать на современных десятичных счётах удобно только на одноразрядное число.
Дощаный счёт состоял не из одной, а из нескольких секций (счётных полей) [7], что позволяло умножить отложенное число на многоразрядное число. В одном счётном поле можно умножать отложенное число на единицы второго множителя, во втором счётном поле на десятки второго множителя, и т.д. А после сложить результат в старшем счётном поле.
Для того чтобы умножать на десятичных счётах достаточно знать таблицу умножения до 9. Умножение происходит со старшего разряда, количество отложенных марок разряда умножается на заданное число. Если получается одноразрядное число, откладывается результат в текущий разряд. Если получается двухразрядное число, откладывается количество марок, равное количеству единиц младшего разряда числа, а в старший разряд добавляется количество марок, равное количеству единиц старшего разряда полученного числа. Для того чтобы умножить число на десять, необходимо просто переместить все отложенные марки на один разряд вверх, такая операция в современной компьютерной терминологии называется сдвиг. Для того чтобы разделить число на десять, необходимо осуществить сдвиг марок на один разряд вниз.
Деление идёт сверху вниз. Количество отложенных марок делится на нужное число. Оставляется остаток от деления, а перед этим частное откладывается в старшем разряде. Иногда приходится делить сразу в двух разрядах, результат при этом откладывается в верхнем разряде, а остаток в нижнем. Полученный результат делится на десять. Делить на два и пять можно другим способом. Деление идет снизу вверх. Делится отложенное число, откладывается частное, а в младший разряд откладывается количество долей, которое определяет количество единиц остатка. Не трудно понять, что пять марок младшего разряда выражают 1/2, а две марки младшего разряда 1/5. Конечно, наиболее удобно делить на десятичных счётах на 2 и 5.
Теперь перейдём к реконструкции счётной доски для двоично-пятеричной СС.
Естественно, что такая доска предназначена для соответствующей СС. Несомненно, что уменьшение основания разрядов позволяет проще производить сложение и вычитание, чем на десятичной СД. Также проще и умножать, достаточно помнить таблицу умножения до 5.
До нас дошла иная СД с другим, более компактным расположением двоично-десятичных разрядов.
Так называемые китайские счёты (суаньпань) устроены подобным образом. Только кладутся они набок, двоичными разрядами вниз, и марки откладываются вверх и вниз. Поскольку два соседних двоично-пятеричных разряда могут выполнять функцию одного десятичного, китайцам считают на сауньпане в ДСС.

Китайские счёты (суаньпань)
В так называемых японских счётах (соробан) выброшены марки для переноса разряда. Они также кладутся набок, двоичными разрядами вниз, и марки откладываются вверх и вниз. На соробане японцы считают в ДСС.
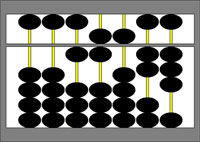
Японские счёты (соробан)
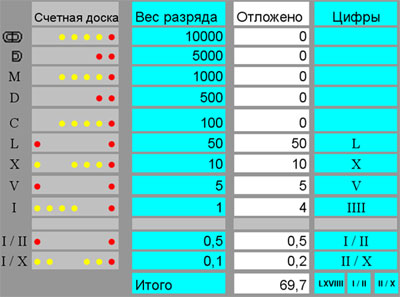
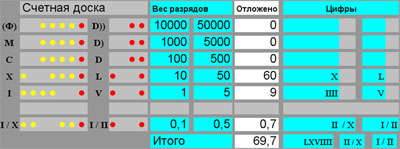
Теперь не трудно реконструировать счётную доску для ВСС.
На данной СД можно выразить цифру 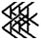 - 60 (см. выше), отложив все марки соседнего шестеричного и десятичного разряда. Шестидесятеричная ПСС удобна для выполнения операций деления на счётной доске и отображения различных дробей, потому что число 60 делится на 2,3,4, 5, 6, 10, 12, 15, 20, 30, 60. Шестидесятеричные доли выражаются следующим образом: ● – 1/60 ●● – 1/30 ●●● – 1/20 ●●●● – 1/15 ● – 1/12 ● – 1/10 ● – 1/6 ●● ● – 1/5 ● ● – 1/4 ●● – 1/3 ●●● – 1/2. Вес марки старшего разряда в шестидесятеричной ПСС: ● – 60 ● – 300 ● – 360 ● – 600.
- 60 (см. выше), отложив все марки соседнего шестеричного и десятичного разряда. Шестидесятеричная ПСС удобна для выполнения операций деления на счётной доске и отображения различных дробей, потому что число 60 делится на 2,3,4, 5, 6, 10, 12, 15, 20, 30, 60. Шестидесятеричные доли выражаются следующим образом: ● – 1/60 ●● – 1/30 ●●● – 1/20 ●●●● – 1/15 ● – 1/12 ● – 1/10 ● – 1/6 ●● ● – 1/5 ● ● – 1/4 ●● – 1/3 ●●● – 1/2. Вес марки старшего разряда в шестидесятеричной ПСС: ● – 60 ● – 300 ● – 360 ● – 600.
И в завершении реконструкция СД для ССМ.
Пока не отложены две правые красные марки во втором разряде, целесообразно использовать только первые четыре жёлтые марки второго разряда. Конечно, для разряда можно использовать только одну сплошную полосу и семнадцать марок для второго разряда, но нам кажется, что это будет менее удобно.
СД обладала одним недостатком: если сумма двух слагаемых в разряде превышала основание разряда, необходимо было произвести вычисления в уме для рассматриваемого разряда. СД пытались усовершенствовать многие изобретатели, наиболее удачным усовершенствованием был счислитель Куммера (СК), изобретённый в 1847 г. нашим соотечественником, петербургским учителем музыки Генрихом Куммером. В СК использовались идеи числительного снаряда Слонимского, однако Куммер упростил этот снаряд [1]. Простота и компактность изобретённого устройства привели к тому, что данный прибор выпускался в нашей стране до 1970 годов ХХ века, но был полностью вытеснен карманными калькуляторами. В каждом разряде в СК имеется металлическая рейка, на которой нанесены десятичные цифры 0-9. Рейку можно двигать вниз и вверх, и таким образом можно отложить или сбросить определённое количество единиц в разряде. Над рейкой имеется специальное окошко, через которое видно только одну отложенную цифру. На каждой половине рейки имеется по восемнадцать зубцов для её передвижения, каждый из восемнадцати зубцов проходит через рейку насквозь и расположен справа и слева рейки. На зубцы наложена прямоугольная маска, через отверстие которой видно только девять активных зубцов. На маске выгравированы 10 цифр, позволяющих выбрать количество добавляемых или сбрасываемых единиц в разряде. Рейка передвигается при помощи металлического штифта, вставленного между зубцами.
При передвижении рейки вниз добавляются единицы разряда, а вверх – сбрасываются. Первые девять зубцов рейки не помечены, остальные зубцы имеют метку. Не помеченный зубец показывает, что рейку нужно передвигать в обычном направлении, через верхнее отверстие маски вниз, а через нижнее – вверх. Помеченный зубец показывает, что рейку нужно передвигать в обратном направлении.
При добавлении единиц метка на зубце говорит о том, что количество добавляемых единиц переполняет разряд и нужно добавить единицу в старший разряд, а в младшем осуществить вычитание. Количество вычитаемых единиц определяется верхним отверстием маски, которое расширено на одну позицию вверх после цифры девять. Если штифтом выбран помеченный зубец напротив цифры девять, то при передвижении рейки вверх произойдет вычитание одной единицы в разряде, если напротив цифры 8 – двух и т.д. Добавление единиц в старший разряд также определяется расширенным отверстием в верхней части маски, которое закруглено и налезает на зубец соседней рейки. Пройдя через это отверстие, штифт сдвинет соседнюю рейку на одну позицию вниз, т.е. добавит единицу в старший разряд.
При вычитании единиц метка на зубце говорит о том, что количество отнимаемых единиц больше отложенных и необходимо произвести заём единицы в старшем разряде, а в младшем осуществить сложение. Количество добавляемых единиц определяется нижним отверстием маски, которое расширено на одну позицию вниз после цифры девять. Если штифтом выбран помеченный зубец напротив цифры девять, то при передвижении рейки вниз произойдет добавление одной единицы в разряде, если напротив цифры 8 – двух и т.д. Заём единиц в старшем разряде также определяется расширенным отверстием в нижней части маски, которое закруглено и налезает на зубец соседней рейки. Пройдя через это отверстие, штифт сдвинет соседнюю рейку на одну позицию вверх, т.е. отнимет единицу из старшего разряда.
Таким образом, Куммер сумел полностью автоматизировать сложение и вычитание на счётной доске. СК был компактнее счёт и совершеннее, но, несмотря на это, профессиональные счетоводы считали гораздо быстрее на счётах. Именно это и было причиной того что СК не смог полностью вытеснить их.
Все современные счётные устройства есть усовершенствование СД.
Литература
- Гутер Р.С., Полунов Ю.Л., От абака до компьютера, –М.: “Знание”, 1982. –208 с.
- В.И. Даль, Толковый словарь живого великорусского языка, в четырех томах, том I, –М.: ОЛМА-ПРЕСС ОАА ПФ “Красный пролетарий”, 2006. –636 c.
- Выгодский М.Я., Арифметика и алгебра в древнем мире, –М.: Наука,1967. –367 с.
- Депман И.Я., История арифметики, –М.: Министерство Просвещения, 1959. –405 с.
- Кузьмищев В., Тайна жрецов Майя, 1968, –357 с.
- Ершова Г. Г., Майя: тайны древнего письма, –М.: Алетейа, 2004. –296 с
- Спасский И. Г. Происхождение и история русских счётов // Историко-математические исследования, –М.: ГИТТЛ, 1952. № 5. 269-420 с.
- Тихвинский В.И. Предыстория автоматизации вычислений в докомпьютерную эпоху // V Международная научно-практическая конференция им. А.И. Китова, Москва, 2015
Примечания.
1. Вторая марка откладывается в десятичном разряде.
5 июля 2015