Из опыта реализации языка программирования Алгол 68 в Ленинградском государственном университете
Мартыненко Борис Константинович
Введение.
Изучение первоначальных вариантов языка программирования АЛГОЛ 68 [1] и подготовка к его реализации начались cосени 1968 г. под научным руководством Г. С. Цейтина, заведующим лабораторией математической лингвистики НИИММ. В течение 1969-75 годовбыла разработана и сдана техническая документация [2] на первый вариант компилятора на основе “Пересмотренного сообщения об алгоритмическом языке АЛГОЛ 68” для машин ЕС ЭВМ (по заказу НИИЦЭВТМинрадиопрома). Автор (руководитель лаборатории системного программирования ВЦ ЛГУ на общественных началах) при проектировании анализирующей части компилятора использовал опыт научной стажировки в A/S Regnecentralen (Копенгаген, Дания), где изучал проект компилятора GIERALGOL-4 под руководством П. Наура.
Г. С. Цейтин предложил модель синтаксического анализа, основанную на автоматных грамматиках и скобочных структурах.Отправной точкой при разработке метода послужила простая модель: регулярные выражения как средство описания языка, и конечные автоматы в качестве адекватного средства его распознавания.
Конечные автоматы часто используют в качестве драйверов для преобразования регулярных языков [3], выполняемых во время сканирования входного текста. Логично было бы найти метод получения конечного автомата с минимальным числом состояний для языка, заданного регулярным выражением, не забывая, однако, что минимизация сужает семантический контекст выше упомянутых преобразований.
Две теоремы из [4] дают ключ к решению проблемы минимизации конечных детерминированных автоматов.
Во-первых, Теорема 3.1 утверждает, что если отношение эквивалентности R, определённое через язык L⊆Σ∗ следующим образом: (∀x, y∈Σ∗) : xRy⇔(∀z ∈Σ∗) : (xz ∈ L⇔ yz ∈ L), имеет конечный индекс, то язык L принимается некоторым dfa. Доказательство этой теоремы конструктивно: строится dfa M, в роли состояний которого используются классы эквивалентности отношения R.
Во-вторых, в Теореме 3.2 утверждается, что этот конечный автомат M является минимальным по числу состояний.
Идея состоит в том, чтобы перенести отношение эквивалентности R, определённое на цепочках в алфавите регулярного языка L, на аналогичное отношение эквивалентности R, определённое на состояниях автомата, а затем использовать классы эквивалентности Rвместо состояний исходного автомата. Именно, два состояния pи qэквивалентны в отношении R, если множества цепочек во входном алфавите автомата, принимаемых в этих состояниях, одинаковы (см. Определение 5).
Итак, как следствие вышеупомянутых теорем, заключаем, что конечный автомат с минимальным числом состояний может быть получен в три этапа:
(1) построение отношения эквивалентности R на множестве состояний данного автомата, исходя из неразличимости цепочек, принимаемых в соответствующих состояниях,
(2) построение классов эквивалентности в отношении R, и
(3) использование классов эквивалентности отношения R взамен состояний данного автомата.
В Разделе 1 описывается алгоритм построения отношения R и классов эквивалентности в этом отношении. Он реконструирован из программы ТК SYNTAX[5], написанной в конце 70-х на Алголе 68, в частности, с цепью тестирования первой версии компилятора.
В Разделе 2 описывается метод Хопкрофта[6], в котором классы эквивалентных состояний строятся, исходя другого отношения ≡, основанного на различимостимножеств цепочек, принимаемых в соответствующих состояниях.
В Разделе 3 оба метода сравниваются на примере регулярного языка, распознаваемого конечном автоматом, позаимствованным из [7] (Ch. 2, pp. 45-46). Этот язык определяется регулярным выражением. По нему строится конечный автомат. Он, как оказывается, не является минимальным по числу состояний. Однако оба метода минимизации этого автомата при использовании этих двух разных отношений дают один и тот результат.
Альтернативный метод минимизации числа состояний
Считая, что основные понятия теории формальных языков и автоматов известны, определим только необходимые.
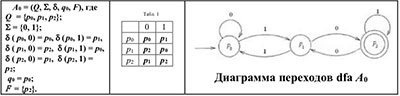
Определение 1. Детерминированный конечный автоматесть формальная система M= (Q, Σ, δ, q0, F), где Q - конечное множество состояний, Σ - входной алфавит, δ : Q x Σ ⟶ Q - функция переходов, q0 - начальное состояние, F⊆Q - множество конечных состояний.
Когда функция переходов всюду определена, говорят, что автомат полный.
Слово (цепочка) есть любая конечная последовательность символов a∈Σ.
Пусть Σ∗ обозначает множество слов над алфавитом Σ, а eобозначает пустое слово.
Определим расширенную функцию переходов δˆ: Q x Σ∗ ⟶ Q следующим образом: δˆ (q, e) = q, δˆ (q, xa) = δ (δˆ (q, x), a), где x ∈ Σ∗, a ∈ Σ.
Определение 2. Язык, T(M), принимаемый автоматом, есть множество всех слов w∈Σ∗ таких, что δˆ (q, w) ∈ F.
Определение 3. Dfa M будем называть приведённым, если
(1) (∀q∈Q): (∃(x∈Σ∗): (δ(q0,x) = q), (2) (∀p∈F): (∃y∈Σ∗) : (δ(q0, y) = p).
Термин «приведённый» в применении к автомату, аналогичен этому термину в применении к грамматикам Хомского, в том смысле, что все нетерминальные и терминальные символы используются при порождении языка, и только они. В применении к конечному автомату это означает, что всё множество цепочек, принимаемых автоматом, задействует все его состояния и входные символы, и только их.
Однако это не значит, что не может существовать другая грамматика типа 3 с меньшим числом нетерминалов, порождающая тот же самый язык. Аналогично, не исключено, что данный регулярный язык может приниматься другим автоматом с меньшим числом состояний.
Определение 4. Пусть M= (Q, Σ, δ, q0, F) – приведённый dfa. Состояния p, q∈Q будем называть подобными, и писать p~q, если
(((p∈F) ∧ (q∈F)) ∨ ((p⋶F) ∧ (q ⋶F))) ∧ ((D(p) = D(q)),
где D(p), D(q) – множества допустимых входных символов a∈ Σ в состоянии pи qсоответственно.
Определение 5. Пусть M= (Q, Σ, δ, q0, F) – приведённый dfa, и T(M) = L. Определим отношение эквивалентности R на множестве состояний Q следующим образом:
pRq ⇔ ((D(p) = D(q)) ∧(∀a∈D(p)): δ(p, a) Rδ(q, a)).
Далее даётся описание алгоритма построения отношения эквивалентности на множестве состояний конечного автомата (этап I) и классов эквивалентных состояний в этом отношении (этап II)в стиле программы на языке типа Алгол68 с комментариями.. Подразумевается, что в алгоритме используются операции над множествами, представимыми статическими массивами из целых, пар целых, т. е. элементов вида .index= .struct(.intp, q) или элементов вида .class= [ ] .int, то есть одномерных массивов целых с разным числом элементов, но не больше, чем число состояний автомата. Над значениями вида .indexопределена операция выборки поля (см. строчки 47-49 в Алгоритме 1).
Для пополнения таких множеств новыми элементами используются операции È. При пополнении массивов новыми элементами с помощью присваивания предполагается, что значение правого операнда присваивается левому только в том случае, когда он не равен ни одному элементу массива, представляющее множество соответствующего вида (см. строчки 10, 21, 30, 53 в Алгоритме 1).
Формулы вида #S, где S - обозначает массив, дают число элементовS, значения которых определены.
На этапе Iиспользуются следующие обозначения и представления:
- Автомат представляется матрицей переходов, строчки которой индексируются номерами состояний, а столбцы - входными символами a∈Σ.
- Состояние автомата представляется его номером 1 ≤ i≤ n, где n= #Q―число состояний, причём состояние 1 считается начальным.
- Принимая во внимание рефлексивность и симметричность отношения эквивалентности R, оно, ради экономии памяти, представляется статическим массивом E[1: e] .index, элементами которого являются пары номеров состояний (p, q), где p < q,называемые гипотезами. Гипотеза представляется как значение вида .index. Число элементов в массиве Eоценивается по формуле e= (n(n+ 1))/2.
- Понятие подобности состояний pи qпереносится на гипотезы h = (p, q) с помощью формулы ~h, которая реализует проверку подобности состояний, составляющих гипотезу h.
- H[1 : #Σ]― массив гипотез, относящихся к парам подобныхсостояний.
- k― индекс текущей (опорной) гипотезы в массиве H.Оператор H[k+:= 1]:= hпополняет множество гипотез в том случае, когда hещё не находится в массиве H.
На этапе II, кроме того, используются следующие обозначения и представления: - CLASS [1:n] .int - элементы текущего класса состояний.
- CLASS INDEX [1:n] .class - индекс классов. Элемент этого массива есть множество состояний исходного автомата, составляющих один класс эквивалентности.
- B[1 : n].int - множество базовых элементов класса.
- A[1 : n].int - множество состояний, включённых во все классы эквивалентности.
Подчеркнём, что в массивах определены только элементы с младшими индексами.
Алгоритм 1. Построение классов эквивалентности в отношении R.
Вход: Приведённый dfa M = (Q, Σ, δ, q0, F).
Выход: CLASSINDEX - множество классов эквивалентности в отношении R.
Метод:
- begin {ЭТАП I: построение отношения эквивалентности на множестве состояний}
- m := 0; { Множество пар эквивалентных состояний (p, q), где p < q }
- for i to n – 1 {1 ≤ i ≤ n, где n = # Q }
- do { i }
- for j from i + 1 to n {j ≤ i + 1≤ n}
- do { j } h := ( i, j ); { Очередная пара состояний: i < j }
- k := 0; {Число элементов в массиве H }
- if (h ∉ E)∧(~ h) {Состояния i и j подобны}
- then { Гипотезы h в E нет. Инициализация массива гипотез: }
- H [k +:=1] := h; {В H теперь только одна гипотеза}
- Continue:= true;
- { Цикл проверки гипотез }
- for I while (I ≤ k) ∧Continue
- do h := H [I] { Перебор гипотез}
- for ∀a∈D(h) { Областьопределениясостояний,составляющихh }
- do h’ := (δ(p of h, a), δ(q of h, a));
- if ~ h’
- then {гипотеза h’ касается состояний
- c одинаковыми областями действия}
- if h’ ∉ H [1: k]
- then H [k +:=1]:= h’ { H пополняется h’ }
- fi
- fi
- od { Конец цикла пополнения гипотез}
- od; { Конец цикла проверки гипотез }
- for I to k
- do
- h := H [I] ;
- if h ∉ E [1 : m]
- then E[m +:= 1]:= h
- fi
- od;
- {Текущий этап пополнение массива E проверенными гипотезами закончен}
- Continue := false
- fi
- od {j}
- od {i};
- {ЭТАП II: построение классов эквивалентности состояний}
- if m > 0 {E ≠∅}
- then
- A := ∅; {Множество задействованных состояний в классах эквивалентности}
- B := {1}; {Инициализация класса начального класса}
- i := 0; {Инициализация индекса классов}
- next : {Цикл построения очередного класса }
- for ∀h: (h ∈E}
- do
- if (p of h) ∈B
- then B := B ∪(q of h)
- elif q of h ∈B then B := B ∪(p of h)
- fi
- od;
- CLASS := B; {Очередной класс}
- CLASS INDEX [i +:=1] := CLASS; {Фиксация класса в индексе классов}
- A := A ∪B; {Фиксациясостояний,включённыхвклассыэквивалентности}
- if #A < #Q
- then {Не все состояния распределены по кассам}
- Continue = true;
- for ∀b: (b ∈Q) while Continue
- do {Цикл нахождения базового элемента следующего класса}
- if b ∉ A
- then B := b; Continue := false
- fi
- od;
- goto next {Возврат на построение следующего класса}
- fi
- fi
- end
Аналог отношения эквивалентности Rпредставлен массивом E. Если при окончании этапаIоказывается, что m= 0, то исходный автомат уже минимальный: каждый класс эквивалентности содержит по одному состоянию исходного автомата. В противном случае множество CLASSINDEXпредставляет классы состояний в отношении эквивалентности R. Подставляя эти классы вместо состояний исходного автомата, мы получаем минимальный автомат, принимающий тот же самый язык.
Метод Хопкрофта построения канонического конечного автомата
Напомним несколько определений и фактов из [6], необходимых для сравнения метода Дж. Хопкрофта и метода, предлагаемого в данной статье, применительно к минимизации детерминированных конечных автоматов.
Определение 6. Пусть M= (Q, Σ, δ, q0, F) — детерминированный конечный автомат, q1, q2∈Q, и q1≠ q2. Считается, что x ∈Σ* различает q1и q2, если (q1, x) ⊢* (q3, ε), (q2, x) ⊢* (q4, ε), и только одно из q3 и q4 принадлежит F.
Говорят, что q1 и q2 k-неразличимы, и пишут q2≡ kq2, если и только если не существует никакого x с | x | ≤ k, который бы различал q1и q2.
Говорят, что состояния q1 и q2 неразличимы по Хопкрофту, и пишут q1≡ q2, если и только если они k-неразличимы для всех k ≥ 0.
Определение 7. Конечный автомат M будем считать приведённым по Хопкрофту, если все состояния достижимы по п. (1) определения 3, и никакие два состояния, q1≠ q2, не различаются по Хопкрофту.
Поскольку отношение неразличимости состояний по Хопкрофту ≡ равнозначно отношению эквивалентности Rпо определению 5, то приведённость конечного автомата по Хопкрофту равнозначна тому, что он минимален по числу состояний.
Алгоритм Хопкрофта [6] (см. Алгоритм 2.2 ниже) построения такого автомата с минимальным числом состояний опирается на следующую
Лемму 2.11. Пусть M= (Q, Σ, δ, q0, F) — конечный автоматсnсостояниями. Состояния q1 и q2неразличимы тогда и только тогда, когда они (n– 2)-неразличимы.
При её доказательстве отмечается, что q1≡ kq2 при двух следующих условиях:
(1) q1≡ 0q2 тогда и только тогда, когда q1и q2 оба либо принадлежат, либо не принадлежат F, и
(2) q1≡ kq2 тогда и только тогда, когда q1≡ k− 1q2 и δ(q1, a) ≡k− 1δ(q2, a) для всех a∈Σ, из чего следует, что ≡ ⊇≡ n − 2⊇≡ n − 3⊇... ⊇≡ 2⊇≡ 1⊇≡ 0.
Справедливость леммы следует из того, что отношение эквивалентности ≡ 0 грубо разбивает Q на два класса эквивалентности Fи Q − F. Затем, если ≡ k+ 1≠ ≡ k, то ≡ k+ 1 является строгим уточнением ≡ k, т. е. ≡ k + 1 содержит, по крайней мере, на один класс эквивалентности больше, чем ≡ k. Поскольку существует самое большее n−1 элементов либо в F, либо в Q − F, мы можем иметь не больше n − 2 последовательных уточнений ≡ 0. Если для некоторого k имеется равенство ≡ k+ 1= ≡ k, то ≡ k+ 1= ≡ k+ 2... по (2). Таким образом, ≡ есть первое отношение ≡ k такое, что ≡ k + 1= ≡ k.
Алгоритм 2.2. (Хопкрофт). Построение канонического конечного автомата.
Вход: Конечный детерминированный автомат M = (Q, Σ, δ, q0, F).
Выход: M’ — приведённый по Хопкрофту (см. Определение 7) конечный автомат, эквивалентный автомату M.
Метод:
Шаг 1: Исключить из автомата M все состояния, не достижимые из q0.
Шаг 2: Строить отношения эквивалентности ≡ 0, ≡ 1, ... , как описано в лемме 2.11, до тех пор, пока не совпадут ≡ k + 1= ≡ k при некотором k. Взять в качестве ≡ отношение ≡ k.
Шаг 3: Построить конечный автомат M’= (Q’, Σ, δ’, q0’, F’ ), где
(3.1) Q’— множество классов эквивалентности отношения ≡, где [p] — класс эквивалентности отношения ≡, содержащий состояние p;
(3.2) δ’([ p], a) = [q], если δ( p, a) = q;
(3.3) q0’= [q0];
(3.4) F’= {[q] | q∈F}.
Можно непосредственно доказать, что шаг 3.2 непротиворечив, т. е. какой элемент класса [p] не взять, значение δ’([ p], a) будет одним и тем же классом.
Доказательство равенства L(M) = L(M’) просто. Его можно найти во многих учебниках[1].
Остаётся убедиться в том, что автомат с меньшим числом состояний, чем у M’, не может допускать L(M). Теорема 2.6 из [6] даёт убедительный ответ на справедливость этого утверждения.
Теорема 2.6. Автомат M’, который строится алгоритмом 2.2, имеет наименьшее число состояний среди всех конечных автоматов, допускающих язык L(M).
Доказательство
Предположим, что M’’, имеет меньше состояний, чем M’, и что L(M’’) = L(M). В силу шага 1 алгоритма 2.2 каждое состояние M’ достижимо. Так как M’’ имеет меньше состояний, чем M’, то найдутся цепочки w и x, переводящие состояние q0’ в разные состояния, а q0’’(начальное состояние автомата M’’ ) в одно и то же:
(q0’’, w)⊢*M''(q, ε) и (q0’’, x)⊢*M''(q, ε).
Следовательно, wи xпереводят автомат Mв различные состояния, скажем, p и r. Это значит, что существует такая цепочка y, такая что только одна из цепочек wyиxy принадлежит L(M). Но wy и xy должны переводить M’’ в одно и то же состояние s, для которого (q, y)⊢*M'' (s, ε). Таким образом, точно одна из цепочек wy и xy не может принадлежать L(M’’ ), а это противоречит предположению о том, что L(M’’ ) = L(M).
Пример: сравнение с методом Хопкрофта
С целью сравнения Алгоритма 1 (см. раздел 1) с Алгоритмом 2.2 Хопкрофта [6], выполним его на примере языка, распознаваемого автоматом A0, позаимствованного из [7] (Ch. 2, pp. 45–46) (см. Рис. 1 ниже).
Автомат A0 читает цепочки символов 0 и 1 и распознаёт их как двоичные числа, конгруэнтные 2 (по модулю 3). Обозначение вида v3(x) представляет бинарную цепочку xкак целое неотрицательное значение по модулю 3.
Например, v3(100) = 1 и v3(1011) = 2.
Рассмотрим произвольную входную цепочку w= a1... anна входе A0, где каждый ai(1 ≤ i ≤ n) есть или 0 или 1. Ясно, что для каждого i цепочка a1... ai попадает в один из этих трёх случаев: (0) v3(a1... ai) = 0, (1) v3(a1... ai) = 1 и (2) v3(a1... ai) = 2. Никакие другие случаи невозможны. Так что A0 нуждается только в трёх состояниях, которые соответствуют вышеупомянутым трём случаям. Обозначим эти три состояния p0, p1 и p2 соответственно. Состояние p0, соответствующее случаю (0), является стартовым, состояние p1соответствует случаю (1), состояние p2, соответствующее случаю (2), является конечным. Правила, которые управляют изменениями состояний, должны быть определены соответственно.
Заметим, что v3(a1 ... ai+ 1) = 2 ∗v3(a1... ai) + ai+ 1(mod3). Так, если текущее состояние есть p1 и текущий входной символ есть 1, то следующее состояние есть p0, поскольку 2 * 1 + 1 = 0 (mod 3). Ясно, что каждый шаг изменения состояния единственным образом определён текущим состоянием и текущим входным символом. Мы выделяем состояние p2 как конечное состояние и определяем, что A0 принимает вход w, если он находится в состоянии p2 после чтения последнего символа w. Очевидно, что dfa A0 является минимальным по числу состояний. Он представлен на Рис. 1.
Теперь мы проделаем следующий эксперимент в три этапа.
(1) Построим регулярное выражение для языка, распознаваемого dfa A0 :
(0 ; 1 , 1)* , 1 , 0 , (1 ; 0, (1 , 0* , 1)* , 0)∗ (*)
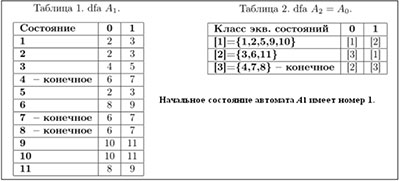
(2) По регулярному выражению (2) простоим dfa A1 (см. Табл. 1 на Рис. 2), который имеет большее число состояний, чем dfa A2 (см. Табл. 2 на Рис. 2).
(3) Используя выше описанный алгоритм 1 (этап 1) получения отношения Rна состояниях A1, построим dfa A2, заменяя состояния A1на классы эквивалентности этого отношения. Получаем dfa A2, который, как видим, равен автомату dfa A0.
Обратимся к Алгоритму 2.2 из [6] и продемонстрируем его выполнение на автомате A1, построенном из регулярного выражения (*) (см. Табл. 1 на рис. 2).
Сначала вычислим отношение ≡, строя последовательность приближений ≡ k, начиная с k= 0. Следуя Алгоритму 2.2, разобъём всё множество состояний данного автомата на два подмножества в соответствии с Леммой 2.11: {4, 7, 8} и {1, 2, 3, 5, 6, 9, 10, 11}. В первое включены все конечные состояния, во второе — все остальные. Они представляют начальное приближение классов эквивалентности отношения ≡.
Ход разбиения множества состояний автомата A1 на подмножества приближений к классам эквивалентности в отношении ≡, представлен в таблице 3.

Таблица 3
Итак, ≡ 1= ≡ 2= ≡, и процесс нахождения классов эквивалентности в отношении ≡ автомата A1закончен.
Заметим, что множество классов эквивалентных состояний автомата A1, полученное в отношении ≡ при помощи Алгоритма 2.2, равно такому же множеству в отношении R={(1, 5), (1, 9), (1, 10), (2, 5), (2, 9), (2, 10), (3, 6), (3, 11), (4, 7), (5, 10), (6, 11), (7, 8), (9, 10)}, полученному посредством Алгоритма 1.
Замена состояний в матрице переходов автомата A1 (Рис. 2, Табл. 1) на классы эквивалентности отношения ≡ или Rдаёт матрицу переходов автомата A2 (Рис. 2, Табл. 2), равную матрице переходов автомата A0 с минимальным числом состояний априори.
Заключение
Алгоритм 1 и Алгоритм 2.2 Дж. Хопкрофта [6] базируются на использовании классов эквивалентности по признаку неразличимостиили различимостимножеств цепочек, принимаемых в соответствующих состояниях, соответственно.
Первый из этих алгоритмов непосредственно строит отношение как множество пар неразличимыхсостояний по движениям автомата, а классы эквивалентности получаются в результате транзитивного замыкания этого отношения.
Второй алгоритм, начиная с грубого разделения состояний на два подмножества, первое из которых включает все конечные состояния, а второе - все остальные состояния, и затем уточняет это разбиение путём перераспределения состояний по признаку различениясоответствующих переходных состояний.
Иначе говоря, эти алгоритмы основываются на двойственных методах и могут иметь разные предпочтения при их реализации. Например, в случае, когда автомат минимальный или близкий к минимальному, то есть основание полагать, что Алгоритм 1 даст ответ быстрее Алгоритма 2.2, поскольку он получит результат уже по признаку подобия(~), который аналогичен признакуразличиястепени 0 (≡ 0).
Реализация этих двух алгоритмов имеют схожую оценку сложности порядка knlogn, где k - некоторая константа, линейно зависимая от размера входного алфавита, а n - число состояний конечного автомата [8].
Литература
- Пересмотренное сообщение об Алголе 68. / Ред. А. Ван Вейнгаарден. М.:«Мир», 1979.
- Алгол 68. Методы реализации / Ред. Г.С. Цейтин. Л.: Изд-во Ленингр. ун-та, 1976. 224 с.
- Мартыненко Б. К. Челночные трансляции в SYNTAX-технологии. // Компьютерные инструменты в образовании, 2014. № 5. С. 3–15.
- Hopcrort J. E., Ullman J. D. Formal languages and their relations to automata. 243 p. Addion-Wesley publishing company, 1969.
- Мартыненко Б. К. Синтаксически управляемая обработка данных. Санкт-Петербург: Издательство Санкт-Петербургского университета, 2004. 316 С.
- Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. Том.1: 613 с. М.: Изд-во «Мир», 1978.
- Rozenberg G., Salomaa A. Handbook of Formal Languages. Vol.1: Word, Language, Grammar, 873 p. Berlin, Heidelberg: Springer-Verlag, 1997.
- Hopcroft J. E. An nlog nalgorithm for minimizing states in a finite automaton. Technical Report CS-71-190, Stanford University, January 1971.
Примечания.
1.См., например, [4].
Материалы международной конференции Sorucom 2017
Помещена в музей с разрешения автора
7 мая 2018