Счислитель для римской системы счисления

В.И. Тихвинский

Надо обладать достаточной смелостью, что бы в XXI веке начать проектировать счётное устройство для непозиционной системы счисления на основе идей Куммера. Тем не менее, данная задача была решена в настоящее время, и получилось устройство, которое демонстрирует древнеримский счёт. Перед тем, как перейти к рассмотрению данного устройства, погрузимся немного в историю.  

Простейшим вычислительным устройством является счётная доска. Счётная доска представляла собой доску, разделённую на счётные полосы, в которых откладывались счётные марки [1,2] (рисунок 1).

Известная всем нам в быту, да и в науке, общепринятая десятичная система счисления не всегда была позиционной. Но непозиционная система счисления может иметь такое же основание, как и позиционная. Именно это и было представлено в египетской десятичной системе счисления[1]. Счётная доска для указанной системы могла выглядеть как на рисунке 1, с той разницей, что на ней счётные марки не метились соответствующими символами цифр. Марки откладывались в левую сторону и сбрасывались в правую. Счётных марок в ней девять по количеству цифр в разряде. Т.к. египетская система счисления была не позиционной, для каждого разряда был разработан элемент цифры, обозначающий единицу разряда, десятку, сотню и т.д.

Цифра могла содержать от одного до девяти элементов [3], что явствует из рисунков 1-2. Как видно из рисунка 1-2, если в разряде счётной доски ничего не было отложено, то цифру соответствующего разряда и не записывали на папирусе или другом носителе. Поскольку на счётной доске рисунка 1 ничего не отложено в миллионном разряде, поэтому нет соответствующей цифры и на рисунке 2.

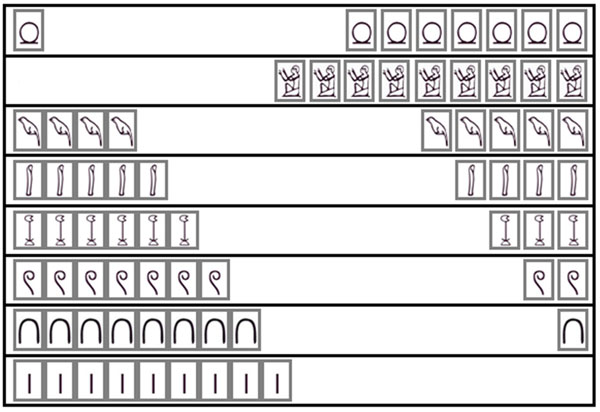
Рис. 1. На Египетской счётной доске отложено десятичное число 10456789.

Рис. 2. Представление современного числа 10456789 в египетской системе счисления.

Большое число элементов в цифре создает определённые сложности при их подсчёте и записи. Для упрощения подсчёта количества единиц разряда приходится разбивать его на четвёрки и тройки (Рис. 2). Для уменьшения количества элементов в цифре были созданы другие системы счисления отличные от египетской системы. В этих системах, чтобы сократить количество единиц в десятичном разряде, его разбивали на два сдвоенных разряда. Данное деление было и в римской системе счисления (см. рис. 3).

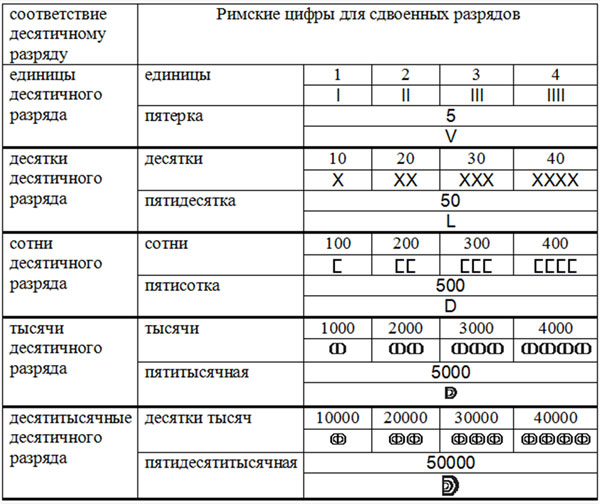
Рис. 3. Соответствие десятичным разрядам цифр римской системы счисления

По таблице, представленной на рис. 3, не трудно заметить геометрический принцип, используемый для построения римских цифр. Единица это линия, пятёрка острый угол, десятка два острых угла. Пятидесятка на рис. 3 прямой угол, сотня два прямых угла. Для упрощения написания, цифра обозначающая сотню, стала обозначаться латинской буквой C(Centum). Пятисотка на рис. 3 это полукруг, а тысяча, полный круг из двух полукругов. Для упрощения написания, цифра обозначающая тысячу, стала обозначаться латинской буквой M(Mille). Далее количество кругов и полукругов в элементах цифр нарастало.  

Для откладывания в разряде счётной доски четырёх единиц, десятков, сотен и т.д., использовалось от одной до четырёх марок счётной доски (рис. 4), им соответствовали цифры для единиц, десятков, сотен и т. д. (рис. 3). Для откладывания пятерки, пятидесятки, пятисотки и т.д., использовалась только одна марка счётной доски (рис. 4), им соответствовали цифры, состоящие только из одного элемента (рис. 3). Если в двух сдвоенных разрядах счётной доски было отложено значение больше, чем пятёрка, пятидесятка и т. д., цифра общего разряда содержала различные по написанию элементы. Десятичная цифра 9 в римской системе счисления записывалась так VIIII, а десятичное число 60 так LX, а десятичное число 69 так LXVIIII (рис. 4).

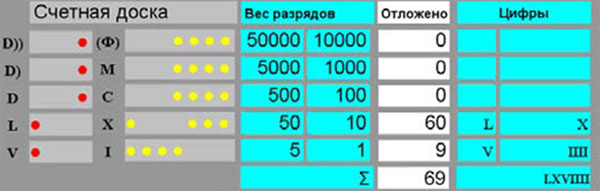
Рис. 4. Счётная доска, веса разрядов и т. д. На счётной доске отложено десятичное значение 69.

Сокращённые записи римских цифр IV (а не IIII), IX(а не VIIII) и т. д. не предназначены для вычислений [4]. Доказательством того, что сокращённая запись римских цифр появилась позже, может служить древнеримский календарь с соответствующими цифрами (рис. 5).

Счётная доска обладает одним недостатком, она не показывает цифрами число, отложенное в разряде, не показывает, сколько нужно оставить счётных марок в разряде при переполнении разряда. Все эти трудности были решены в счислителе Куммера[5]. На основе счислителя Куммера был разработан упрощённый счислитель для римской системы счисления, в котором четыре разряда. Счётные рейки счислителя представлены на рис. 6.

Рис. 5. Древнеримский каменный календарь III-IV(IIII) нашей эры.

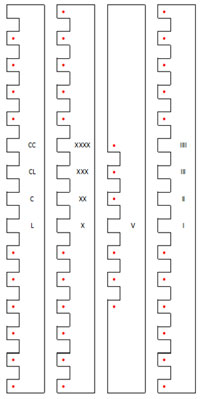
Рис. 6. Счётные рейки для счислителя.

Старший разряд счислителя расширенный, поэтому в нём можно отложить не только значения пятьдесят (L), но и значение сто (С), сто пятьдесят (CL) и двести (CС), что видно из цифр на счётной рейке.

Низ счислителя представляет собой короб, который состоит из чёрного прямоугольного основания и серой секционной рамки, прикрепленной к основанию. Счетные рейки помещаются в секции рамки и могут двигаться вверх вниз по секции (рис. 7).

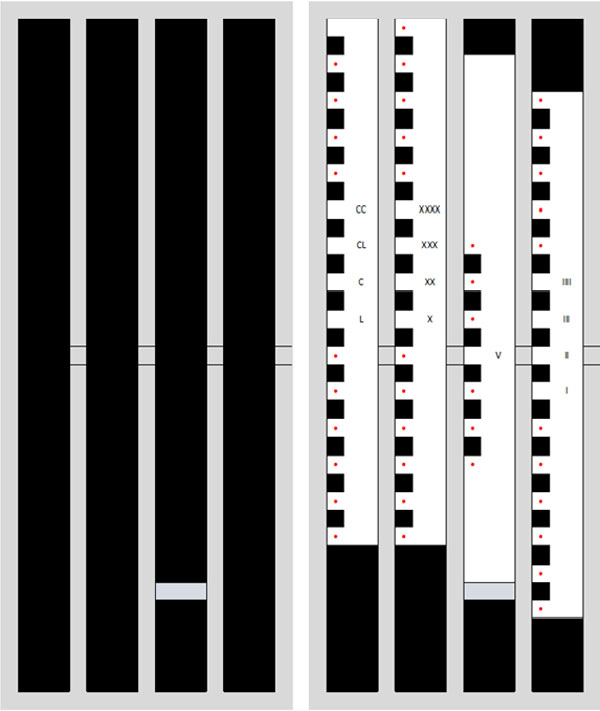
Рис. 7. Короб и счётные рейки в коробе.

На рамку сверху накладывается маска с прорезями для счетной палочки и с прорезями для отображения отложенных цифр на счётной рейке. На маске также отображены значения в виде цифр без знака и цифр со знаком минус, которые будут прибавляться или вычитаться в соответствующем разряде (рис. 8).

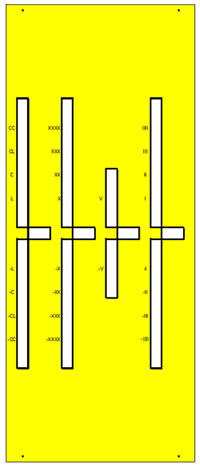
Рис. 8. Маска счислителя

На рис. 9 показано фото счислителя, на котором отложено десятичное значение 29 (XXVIIII). Справа от счислителя прикреплена счётная палочка, которую легко вынуть из держателя.

Если вставить кончик счётной палочки между зубцами счётной рейки (см. рис. 9) в соответствующем разряде напротив цифры X и двигать её вниз до конца через прорезь в маске, то счётная рейка передвинется на две позиции вниз (на один зубец и промежуток между ним), и в окошке разряда отобразится цифра XXX. Это не трудно увидеть из рис. 6, посмотрев на соответствующую рейку.

Рис. 9. Счислитель в сборе.

Теперь о переносе разряда, пусть наш счислитель будет в состоянии как на рис. 9. И мы хотим к двадцати девяти XXVIIII прибавить пять V. Но разряд для пятерки переполнен. Если мы вставим кончик счётной палочки в прорезь маски в соответствующем разряде напротив цифры V, то мы увидим, что она расположена между двумя зубцами помеченными точками. Это значит, что рейку счётной палочкой надо тянуть не вниз до упора, а вверх до упора, это приведёт к смещению счётной рейки на две позиции вверх, при этом в окошке будет пустота, т. е. не будет отражено цифр, иными словами, разряд будет сброшен. Это не трудно увидеть из рис. 6, посмотрев на соответствующую рейку. После сброса разряда, нам будет необходимо добавить десятку в старший разряд, что рассмотрено в предыдущем абзаце данной статьи. При этом на счислителе будет отражено в соответствующих разрядах тридцать четыре XXXIIII.

Теперь о вычитании. Пусть наш счислитель будет в состоянии как на рис. 9. И мы хотим из двадцати девяти XXVIIII вычесть один I. Вычитание на счислителе аналогично сложению, только счётные рейки тянутся в противоположном направлении. Если вставить кончик счётной палочки между зубцами счётной рейки в соответствующем разряде напротив цифры со знаком минуc -I, и двигать её вверх до конца, через прорезь в маске, то счётная рейка передвинется на две позиции вверх, и в окошке разряда отобразится цифра III. Это не трудно увидеть из рис. 6, посмотрев на соответствующую рейку. При этом на счислителе будет отражено в соответствующих разрядах двадцать восемь XXVIII. Таким образом, на счислителе можно осуществлять сложение и вычитание.

Литература

1. Тихвинский В.И., В.В. Холмогоров. Системы счисления в древности и современности, International Journal of Open Information Technologies ISSN: 2307-8162 vol. 10, no. 6, 2022.

2. Тихвинский В.И., Предыстория автоматизации вычислений в докомпьютерную эпоху, –М.: Менеджмент и бизнес-администрирование, №3, –2015 –199-202 с.

3. Выгодский М.Я., Арифметика и алгебра в древнем мире, –М.: Наука, –1967. –367 с.

4. Депман И.Я., История арифметики, –М.: Министерство Просвещения, –1959. –405 с.

5. Тихвинский В.И., Уравновешенная (симметричная) троичная система счисления и её использование в вычислительных устройствах в докомпьютерную и компьютерную эпоху https://computer-museum.ru/articles/precomp/1375

Об авторе: Тихвинский Виталий Игоревич,
старший преподаватель кафедры информатики,
Российский экономический университет имени Г.В. Плеханова,
E-mail: tvitaly1@yandex.ru.
Помещена в музей с разрешения автора 28 ноября 2022