Счётный прибор Прюво ле Гюэ

Дмитрий Златопольский

Счётный прибор – так называемые «палочки Непера» – описан в большом числе источников (см., например, [1]).

В 1890 году француз Прюво ле Гюэ распространил идею Джона Непера на двузначные числа. Свой счётный прибор он назвал «автоматический вычислитель» (фр. «calculateurs automatiques»). С его помощью можно было получать произведение многозначного числа сразу на все однозначные множители.

Рис. 1 Calculateurs automatiques Прюво де Гюэ. Материалы Виртуального Компьютерного Музея

Рис. 1 [2]

Прибор состоял из 50 брусков прямоугольного сечения, на широких гранях которых были записаны произведения каждого из чисел от 0 до 99 на 1, 2, …, 9. На одной стороне бруска изображались произведения для четного числа, на другой — для следующего за ним нечётного (например, 18 и 19, 26 и 27 и т.п.). На рис. 2 показан брусок с гранью для числа 65.

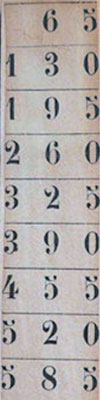
Рис. 2

Бруски, сгруппированные по десяткам чисел, размещались в ящичке, и для удобства поиска нужного бруска на их верхних торцах писались чётные числа, а на нижних — нечётные.

Рис. 3

При расчётах отбирались бруски с двузначным числами (и при необходимости – с однозначными с начальным нулем), образующими множимое. Пример умножения числа 6567 показан на рис. 4.

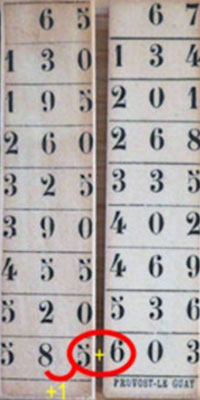
Рис. 4

Результат умножения в каждой строке определялся следующим образом.

Количество сотен в числе на правом бруске складывалось с последней цифрой левого смежного бруска и являлось соответствующей цифрой результата. Например, произведение 6567 на 3 равно 19701 (5 + 2 = 7), на 7 – 45969 (5 + 4 = 9). Если при сложении получалась сумма, большая 9, то количество единиц в ней являлось очередной цифрой результата, а количество десятков – учитывалось в следующем старшем разряде. Например, при умножении числа 6567 на 9 результат равен 59103 (5 + 6 = 11; 8 + 1 = 9).

Можно отметить следующие преимущества счётного прибора Прюво ле Гюэ по сравнению с палочками Непера:

меньшее число операций, проводимых при расчётах (в том числе в уме);
бóльшая наглядность представления результата.

Список использованных источников

Об авторе:

к.т.н., доцент, ГБОУ Школа № 1530 «Школа Ломоносова» (Москва)

16 октября 2023