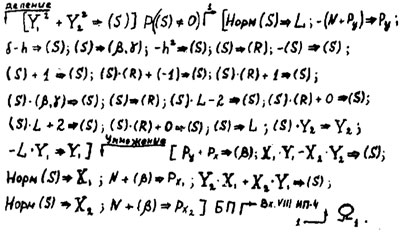Интерпретирующая система для действий с комплексными числами (ИП-4) - часть 2

Г. А. Фурман

§3. Общая характеристика стандартных подпрограмм в системе ИП-4.

Все подпрограммы рассчитаны на работу с плавающей запятой. Основным аргументом стандартной подпрограммы является нормализованная величина u = (X₁ + iX₂)·3^Px, хранящаяся внутри ИП-4. Окончательный результат тоже засылается на место u в нормализованном виде, но это осуществляет подпрограмма «Нормализация», которая расположена в дополнительной зоне и обращение к которой производится через вход VIII ИП-4. Стандартные же подпрограммы выдают результат в виде:

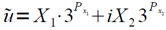
где X₁ и Х₂ — нормализованные величины, расположенные в основной зоне ИП-4, а Р_x1 и Р_x2 их порядки, причем Р_x1 записывается на место Р_x, а Р_x2 записывается в первую половину ячейки, отведенной для величины Y₁. По окончании работы каждая подпрограмма передает управление входу VIII ИП-4, в результате чего вызывается в Ф₀ и выполняется подпрограмма «Нормализация».

Подпрограмма «Нормализация» из двух порядков Р_x1 и Р_x2 выбирает наибольший и записывает его на место Р_x. Величина X_i (i = I или i = 2), имеющая меньший порядок, сдвигается вправо на разность порядков. Если одна из величин X₁, X₂ равна нулю, а другая отлична от нуля, то в ячейку Р_x засылается порядок величины, отличной от нуля.

Примечание. Как было сказано выше, величина v (точнее Y₁) затирается после выполнения подпрограммы, поэтому использовать повторно эту величину без присвоения ей нового значения нельзя. Если X₁-Y₁=0, то на место Р_x засылается минимальный порядок Р_x=40.

В конце подпрограммы «Нормализация» исследуется порядок Р_x. Если Р_x>40, то происходит предупредительный останов Ω₀ по команде 14423, хранящейся в ячейке 003. Этот останов предупреждает о том, что при дальнейших вычислениях возможно переполнение, но этот останов можно игнорировать и продолжать вычисления нажатием кнопки «пуск». Если Р_x<-40, то в ячейки для X₁ и X₂ засылаются нули, и полагается Р_x=-40.

После этой проверки данная подпрограмма передает управление на вход IV ИП-4. Итак, подпрограмма «Нормализация» формирует на месте величины u результат в стандартном нормализованном виде.

Для того, чтобы нормализовать какое-нибудь комплексное число Z, находящееся на магнитном барабане, и записать его снова на магнитный барабан (на место W), нужно обратиться ко второй части подпрограммы «Нормализация», расположенной в зоне II магнитного барабана. Это обращение в общем случае имеет вид:

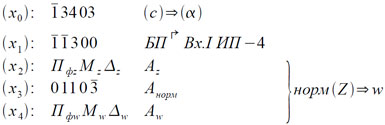
В некоторых стандартных подпрограммах имеются аварийные остановы для случаев, когда операцию нельзя выполнить:

• останов Ω₁, (по команде 1442 3) означает, что требуется выполнить деление на нуль;
• остановы Ω₂ (по команде 00323) и Ω₃ (по команде 12323) означают переполнение при вычислении функций sin u, cos u, e^u, sh u, ch u;
• останов Ω₄ (по команде 00023) означает, что требуется вычислить ln 0 или 1/0.

Библиотека подпрограммы для действий с комплексными числами занимает 12 зон магнитного барабана (с 12 по 21) без ИП-4 и характеризуется таблицей 2:

Таблица 2

*Результаты этих операций представляются также в виде комплексных чисел.

При составлении основной программы можно пользоваться константами, находящимися в основной зоне ИП-4 и перечисленными в следующей таблице:

Кроме того, в зоне 23 и 11 имеются константы, задающие действительные числа в комплексном виде (мнимая часть равна нулю). Над этими константами можно производить все операции в режиме ИП-4, задавая их обобщенные адреса. Эти константы указаны в следующей таблице:

Если стандартная подпрограмма занимает больше одной зоны, то происходят дополнительные обращения к магнитному барабану. Ниже приводится таблица 3, содержащая время выполнения каждой подпрограммы (псевдооперации). Так как это время зависит не только от числа тактов работы машины, но и от времени ожидания нужной зоны магнитного барабана при обращении к нему, (а в данном случае это время может быть точно учтено), то за время Т* выполнения псевдооперации принимается отрезок от момента вызова данной подпрограммы в Ф₀ (исключительно) до момента передачи управления входу 1V ИП-4, т.е.:

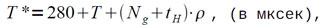
где Т и N_g имеют тот же смысл, что и в таблице I, t_н = 5490 является временем выполнения подпрограммы «Нормализация» (включая передачу ей управления) после вызова зоны M_g в оперативную память, а ρ = 1, если соответствующая подпрограмма по окончании работы обращается к «Нормализации», в противном случае (при обращении сразу к входу IV) ρ = 0. В таблице 3 время T* будет указываться при ρ = 1 в виде явной суммы T *=Δ + t_н, где ΔТ будет кратно 2500 мксек.

Таблица 3.

§4. Подпрограмма выполнения действия типа сложения.

Алгоритм сложения двух чисел

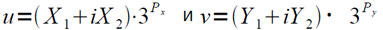
использует соотношение:

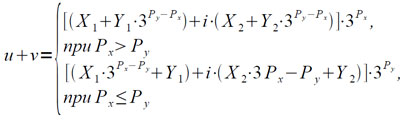
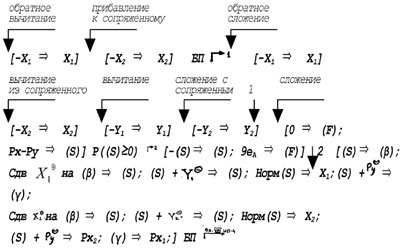
Подпрограмма для реализации действий типа сложения (включая и само сложение) размещена в одной зоне МБ и описывается следующей схемой:

Подпрограмма выполнения действий типа сложения

Подпрограмма выполнения действий типа сложения

§5. Подпрограмма для выполнения умножения и деления.

В данной подпрограмме деление сводится к умножению делимого на обратную величину делителя. Алгоритм умножения двух чисел:

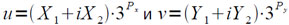
использует соотношение:

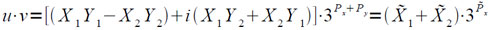
Абсолютная погрешность вычисления мантисс действительной и мнимой частей произведения u·v не превосходит 3^-16.

Обратная величина 1/v определяется при:

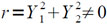
При r = 0 происходит аварийный останов Ω₂ по команде 14423 (адрес команды 041). При этом используются соотношения:

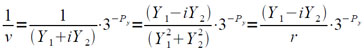
Если положить r = r_н•3^Рr , где r_н — величина, получаемая в результате нормализации r, то получим:

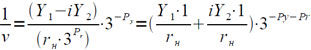
или

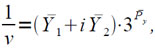
где

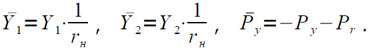
Величина t = 1/r_н вычисляется по итерационной формуле:

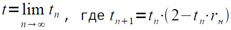
(5.1)

При этом нулевое приближение t₀ получается из соотношения:

если положить r_н = 1 + h, |h|< 1/2.

С погрешностью |ε| < 0,00782 можно определить t по формуле (примем это значение за t₀):

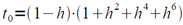
Тогда достаточно сделать две итерации по формуле (5.1), чтобы получить t = t₂ с требуемой точностью.

Действительно, если t_n = t+ε_n, то погрешность (n+1)-ой итерации ε_n+1 с учетом погрешности выполнения умножения определяется по формуле:

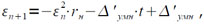
где

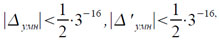
Отсюда

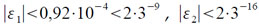
кроме того, величина r, а значит и величина r_н, была вычислена с погрешностью Δr, |Δr| < 3^-16, которая внесет в вычисление величины t дополнительную погрешность:

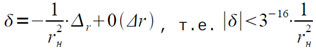
Итак, полная погрешность ε_t вычисления t = 1/r_н удовлетворяет неравенству:

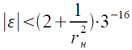
Погрешности ε_Y1, ε_Y2 вычисления величин Y₁ и Y₂ определяются по формулам:

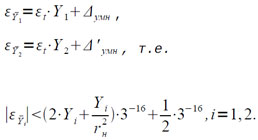
Максимальное значение правой части этого неравенства достигается при Y_i = √(3/2) , r_н = 1/2, а именно:

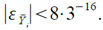
Так как для вычисления u/v используется формула:

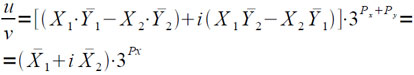
то погрешность вычисления мантисс действительной и мнимой частей результата не превосходит 25•3⁻¹⁶.

Подпрограмма умножения и деления размещается в одной зоне МБ и описывается следующей схемой:

Программа выполнения умножения и деления.

Программа выполнения умножения и деления

Предыдущая часть: Интерпретирующая система для действий с комплексными числами (ИП-4) - часть 1

Следующая часть: Интерпретирующая система для действий с комплексными числами (ИП-4) - часть 3

Литература.

1. Е.А. Жоголев. Система команд и интерпретирующая система для машины «Сетунь». Ж. вычисл. матем. и матем. физ., 1961, I, No3, 499-512.
2. Е.А. Жоголев, О логических структурах и математическом обслуживании малых цифровых автоматических машин. Диссертация на соискание ученой степени кандидата физико-математических наук, МГУ, 1963 г.
3. Е.А.Жоголев. Математическое обслуживание машины «Сетунь». Отчет ВЦ МГУ, 1961 г.

Серия: Математическое обслуживание машины «Сетунь»
16 ноября 2014