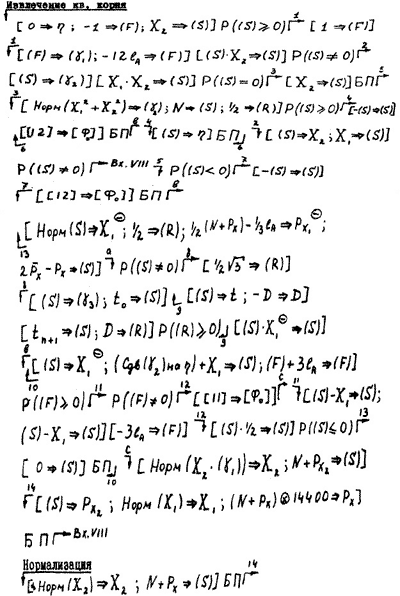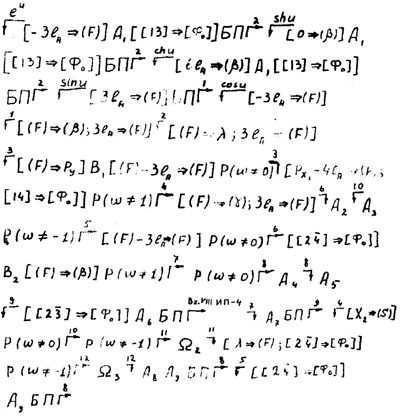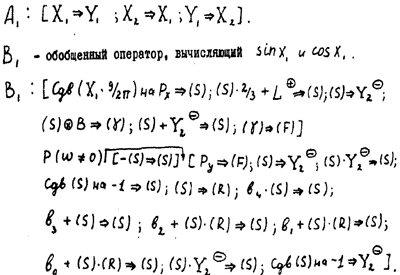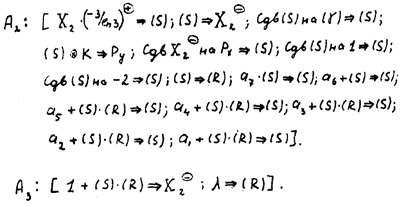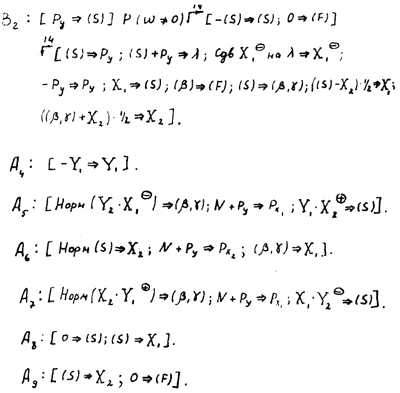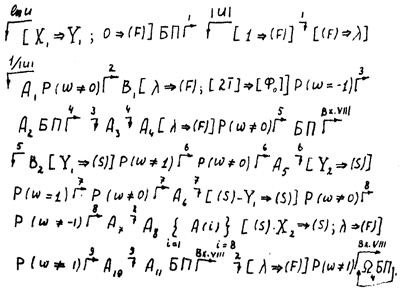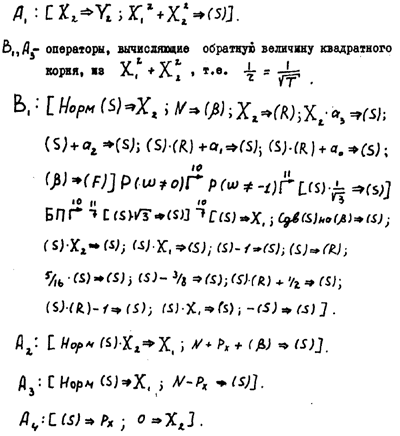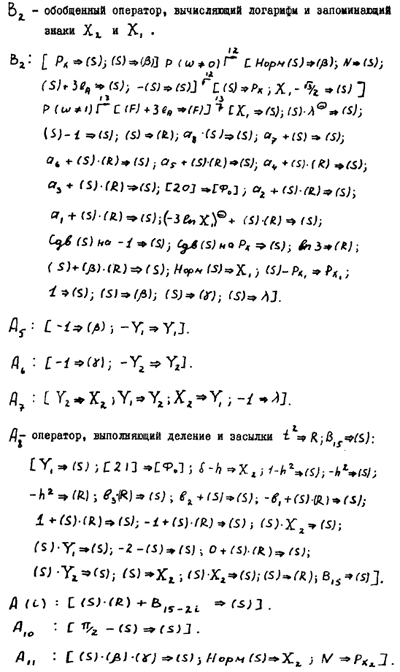Интерпретирующая система для действий с комплексными числами (ИП-4) - часть 3
Г. А. Фурман
§6. Подпрограмма извлечения квадратного корня и нормализация.
Квадратный корень из комплексного числа u = (X1 + iX2)·3Px вычисляется по следующим формулам:
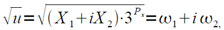
где
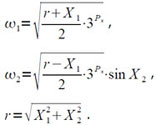
Так как величина r не меньше компонент X1 и X2, то (r± X1)/2 ≥ 0. Однако за счет неточного представления чисел в машине и неточности выполнения операций для малой величины Х выражение (r± X1)/2 может быть равно -ε1 (ε1>0), тогда программа приравнивает значение √((r± X1)/2) к нулю.
Алгоритмы извлечения квадратного корня из действительного числа l = L•3Pl следующие:
a) При l = r2•32Px:
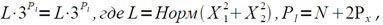
N — число сдвигов при нормализации r2,
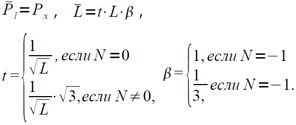
b) При l = (r± X1)/2 •3Px
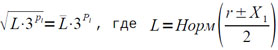
Pl = N + Px,
N — число сдвигов при нормализации (r± X1)/2, Pl = [1/2 Pl – 1/3]бл, L= t•t,
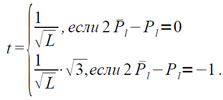
При L=0 полагается L=0 , порядок не вычисляется.
При X22=0 полагается r=|X1|.
При X12=0 полагается r=|X2|.
При X1=0 и X2=0 полагается W1=0 и W2=0.
Величина t в подпрограмме не нормализуется и поэтому удовлетворяет неравенствам:
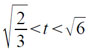
Величина t вычисляется с помощью трех последовательных приближений t0, t1, t2, причем, нулевое и первое приближения вычисляются в качестве коротких слов. Для вычисления нулевого приближения используется два первых члена разложения:
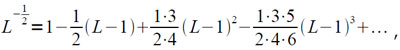
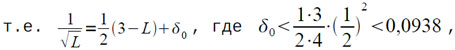
так как L≠0 и 0,5<|L|<1,5. Таким образом,
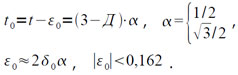
Второе и третье приближения используют преобразованную итерационную формулу (см. [3]), которая из-за погрешности выполнения операции умножения и представления коэффициентов в машине записывается следующим образом:
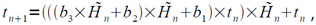
где
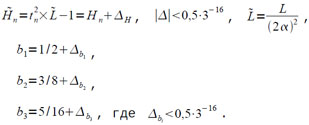
Отсюда
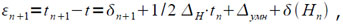
где δn+1 = 35/8 • tn-3 • εn4 – погрешность итерационной формулы, |∆умн|<1/2 • 3-16 – погрешность последнего умножения, Hn ≈ 2•εn•t-1, δ(Hn) — погрешность, включающая все погрешности, содержащие в качестве множителя Hn в какой-либо целой положительной |δ(H0)|<1/2 • 3-16.
Для первого приближения:
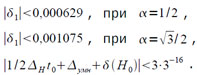
Отсюда
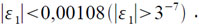
Для второго приближения погрешность δ(Hn) практически равна нулю (|δ(H1)|<0,01 • 3-16, δ2<1010.
Следовательно,
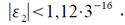
Величина L вычисляется фактически по формуле:
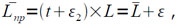
где ε = ε2•L+∆умн, т.е. |ε| < 2,18•3-16. Однако, в суммарную погрешность εL вычисления L будет выходить еще погрешность σ, вносимая погрешность ∆L вычисления величины L:
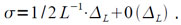
Так как в случае а) |∆L| < 3−16, то σ в этом случае будет удовлетворять неравенству:
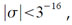
и, следовательно
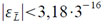
Тогда в случае б) |∆L| < 1,59•3−16
Отсюда

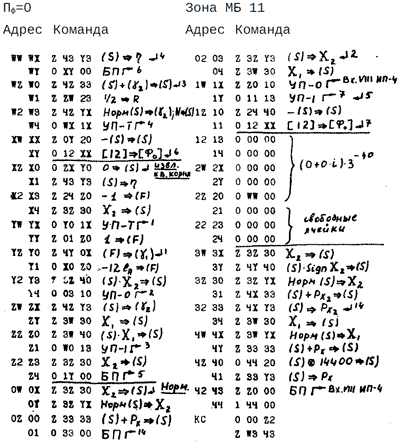
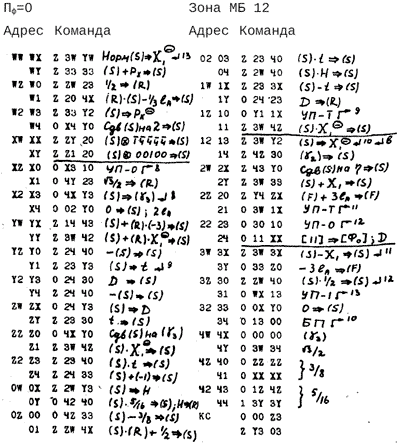
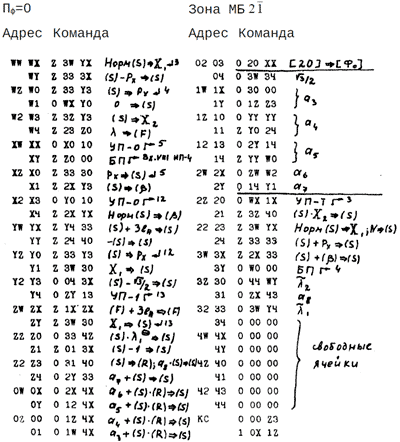
т.е. абсолютная погрешность мантисс W1 и W2 не превосходит 4•3−16. Данная подпрограмма размещается в двух зонах МБ: 11 и 12. Вычисление величины L расположено в зоне 12. Анализ аргумента и переход к Вх.VIII ИП-4 находятся в зоне II. В зоне II расположено также начало подпрограммы, реализующей псевдооперацию нормализации комплексного числа и переход в Вх.VIII ИП-4 для завершения нормализации (точнее: в зоне II производится отдельно нормализация и действительной части, а в подпрограмме «нормализация» эти части приводятся к одному порядку).
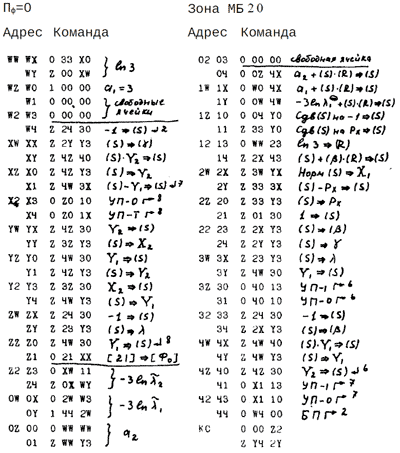
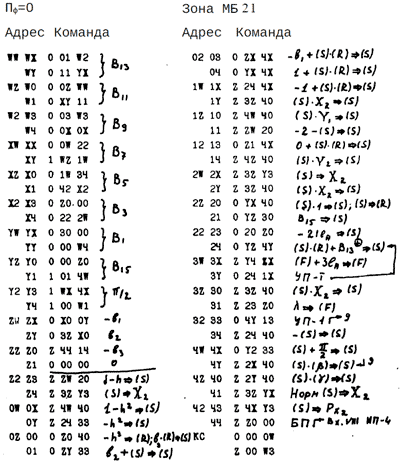
Подпрограмма извлечения квадратного корня и нормализации описывается логической схемой:
В этой схеме γ1 —рабочая ячейка для sign X2 , γ2 —рабочая ячейка для X22 и r2, причем эти величины отстоят в памяти от величины X на 12lA , т.е. запись X1θ, при (F) = −12lA означает (γ2). Содержимое ячейки γ3 используется при вычислении tn+1 . В качестве величины D используется одна из команд программы, причем, первоначально D>0. Величина Px2 хранится в старших разрядах Y1, т.е. состоит в памяти от величины Px на 3lA. Величина t помещается на место λ основной зоны ИП-4.
Два оператора (S) – X1 ⇒ (S), следующие за стрелкой ↴, реализуются в программе одной командой за счет того, что управление по этой стрелке передается длинной ячейке. Последние два оператора относятся к подпрограмме, реализующей псевдооперацию нормализации комплексного числа.
Подпрограмма извлечения квадратного корня и нормализации, I.
Подпрограмма извлечения квадратного корня, II.
§7. Подпрограмма для вычисления функций sin u, cos u, shu, ch u, eu.
Данная подпрограмма занимает 4 зоны на МБ.
Функции вычисляются по следующим формулам:
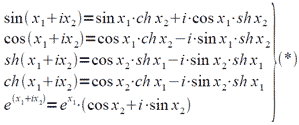
(*)
Алгоритмы для вычисления sin x, cos x, ex (x — действительное число) взяты из работы [3]. Абсолютная погрешность вычисляется каждой из величин 3sinX, 3cosX, мантиссы ex не превосходит 5/2•3−16 при |X|<3/2. Так как
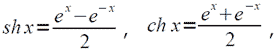
то абсолютная погрешность εshx можно оценить сверху следующим образом:
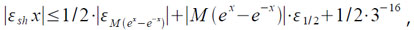
где M (ex − e−x) — мантисса (ex − e−x),
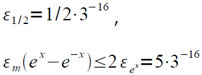
Отсюда получаем (при |x|<3/2):
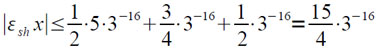
Аналогично:
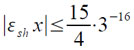
Абсолютные погрешности вычисления мантисс действительной и мнимой частей в каждой формуле (*) состоят из погрешности, которая получается в результате перемножения указанных там величин, и погрешности выполнения умножения, которая не превосходит ½ • 3−16. Эти погрешности не превосходят: 10 • 3−16, а абсолютная погрешность вычисления мантисс действительной и мнимой частей ex1 + iX2 не превосходит: 4 • 3−16.
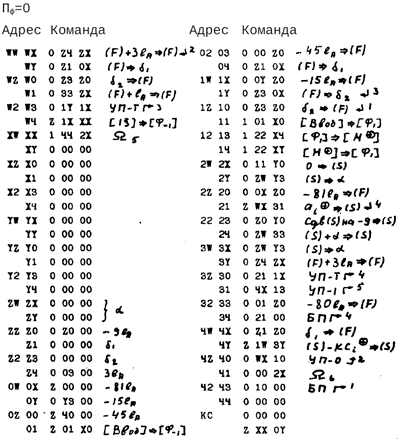
Подпрограмма вычисления функций sinu, cosu, shu, chu, eu, описывается следующей схемой:
Здесь Аi — арифметические операторы, Bi — обобщенные операторы, имеющие нижеследующее содержание:
А2 и А3 — арифметические операторы, вычисляющие ex.
B2 — обобщенный оператор, вычисляющий shx2 chx2.
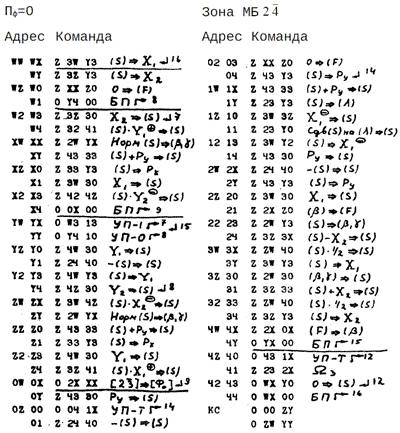
Подпрограмма вычисления функций sin u, cos u, sh u, ch u, eu. I.
Подпрограмма вычисления функций sin u, cos u, sh u, ch u, eu. II.
Подпрограмма вычисления функций sin u, cos u, sh u, ch u, eu. III.
Подпрограмма вычисления функций sin u, cos u, sh u, ch u, eu. IV.
§8.Подпрограмма для вычисления функций ln u, |u|, 1/|u|.
Подпрограмма занимает 4 зоны на магнитном барабане. Функции вычисляются по формулам:
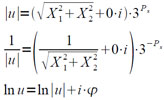
где φ = arctg(X1/X2)+2kπ, но в подпрограмме вычисляется главное значение аргумента φ = arctg(X1/X2)+2kπ (k=0). Кроме того, полученные значения нормализуются. Для извлечения квадратного корня из X12+X22
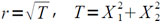
используется алгоритм из [3], но в связи с тем, что аргумент Т вычисляется с погрешностью εT , εT < 3−16 , то погрешность вычислений будет больше, чем в [3].
Величина g = 1/√T при точном аргументе Т вычисляется с погрешностью εg, |εg| < 3−16. Следовательно, абсолютная погрешность ε1/|u| вычисления мантиссы действительной части величины 1/|u| удовлетворяет неравенству:
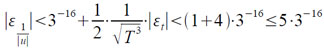
Так как величина r вычисляется по формуле:
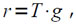
то погрешность εr ее вычисления удовлетворяет соотношению:
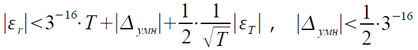
Отсюда
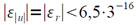
Функции ln x при точном аргументе X вычисляются в [3] с погрешностью εln,
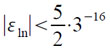
Поэтому абсолютная погрешность εln r вычисления мантиссы действительной части величины ln u удовлетворяет соотношению:
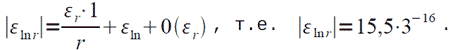
Величина φ = arctg(X1/X2)+2kπ вычисляется согласно следующим соотношениям:
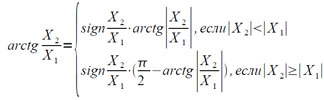
для вычисления отношений t = X1/X2 или t = X2/X1 используется алгоритм деления из [3]. Это отношение вычисляется с погрешностью εt , |εt| < 2 •3−16.
Значение arctg t вычисляется с помощью полинома 15-ой степени:
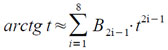
Этот полином получен из разложения arctg t по полиномам Чебышева,
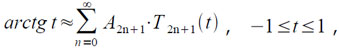
в котором взято восемь членов, что вносит в вычисления погрешность ε,
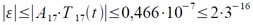
Коэффициенты B2i−1 полинома имеют следующие значения:
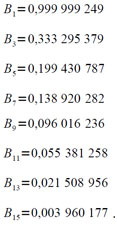
Полная абсолютная погрешность εφ вычисления arctg t с учетом погрешности аргумента t удовлетворяет неравенству:
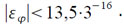
Логическая схема данной подпрограммы имеет следующий вид:
Здесь λ используется в качестве признака того, какую из трех функций нужно вычислять. Первоначально ИП-4 всегда формирует λ<0 (это соответствует тому, что нужно вычислять 1/|u|) . Остальные операторы имеют следующий смысл.
В2 — обобщенный оператор, вычисляющий логарифмы и запоминающий знаки X2 и X1.
Подпрограмма вычисления функций ln u, |u|, 1/|u|, I.
Подпрограмма вычисления функций ln u, |u|, 1/|u|, II.
Подпрограмма вычисления функций ln u, |u|, 1/|u|, III.
Подпрограмма вычисления функций ln u, |u|, 1/|u|, IV.
Приложения.
Ввод системы ИП-4.
Контрольные суммы.
Предыдущая часть: Интерпретирующая система для действий с комплексными числами (ИП-4) - часть 2
Литература.
- Е.А. Жоголев. Система команд и интерпретирующая система для машины «Сетунь». Ж. вычисл. матем. и матем. физ., 1961, I, No3, 499-512.
- Е.А. Жоголев, О логических структурах и математическом обслуживании малых цифровых автоматических машин. Диссертация на соискание ученой степени кандидата физико-математических наук, МГУ, 1963 г.
- Е.А.Жоголев. Математическое обслуживание машины «Сетунь». Отчет ВЦ МГУ, 1961 г.
16 ноября 2014