Прямоугольный или круглый?

Юрий Полунов

Я с детства презирал овал,
Я с детства угол рисовал.

Павел Коган.

Меня, наверно, Бог не звал
И вкусом не снабдил утонченным,
Я с детства полюбил овал
За то, что он такой законченный.

Наум Коржавин.

Трем замечательным немецким самоучкаммеханикам мы обязаны изобретением арифмометров, имевших совершенно новую для счетной техники круглую конструкцию.

Один из них — Якоб Лейпольд — родился 25 июля 1674 г. в Планице, в семье талантливого ремесленникамеханика. Из-за стесненных материальных обстоятельств Лейпольду не довелось много учиться: он слушал некоторое время лекции по математике в Йене, затем штудировал теологию в Виттенберге. Когда деньги, отпущенные ему семьей на обучение, подошли к концу, Лейпольд решил возвратиться в родной город, но, заехав по дороге в Лейпциг, он не удержался от искушения прослушать несколько лекций в университете и изменил свое решение: он снова будет учиться!

Лейпольд поступает в Лейпцигский университет на теологический факультет и одновременно работает как репетиторматематик. Позже он начинает изготавливать на продажу различные приборы и инструменты. Нужен был лишь толчок, чтобы Лейпольд изменил богословию и занялся тем, к чему звало его призвание. Таким толчком оказались слова некоего лиценциата Зелигмана, сказавшего однажды Якобу, что «Лейпциг имеет достаточно проповедников, но ни одного мастера, который поставил бы ремесло на математическую и физическую основу».

Лейпольд решает отказаться от карьеры священнослужителя и стать профессиональным механиком. Так как у него не было денег для открытия мастерской, он решил «поправить обстоятельства женитьбой», выгодной разумеется, и в 1701 г. сочетается браком с дочерью оружейника из Лукка. Тесть выхлопотал для него место эконома в городском госпитале, что позволило Лейпольду жить безбедно и заниматься в свое удовольствие любимой механикой. Он конструировал, изготовлял и продавал в основном «ходовую» продукцию — воздушные насосы. Хотя и медленно, но упорно он шел к своей цели — к собственной мастерской. И такая мастерская у него появилась. Произошло это уже после смерти жены в 1713 г., когда он лишился места эконома в госпитале.

В 1715 г. Якоб Лейпольд зачисляется механиком Лейпцигского университета. Его имя и машины приобретают все большую известность: он удостаивается чести быть почетным членом Академии наук в Берлине, получает титулы прусского коммерческого советника и горного советника польского короля. Последние годы жизни Лейпольд посвящает обучению молодежи основам теоретической и прикладной механики, занимая пост директора технической школы.

Но все же не машины и не преподавательское искусство принесли славу Якобу Лейпольду, а многотомная энциклопедия технических знаний под общим названием «Theatrum machinarium» («Описание различных машин»). Над ней он работал с 1722 г. до самой смерти, наступившей в январе 1727 г. Из девяти томов «Описания...» при жизни автора вышли первые семь. Каждый из них содержал 200 страниц текста in folio и 50 гравюр, скопированных из книг великих инженеров Возрождения — Джероламо Кардано, Жака Бессона, Джуанелло Турриано, Агостино Рамелли и др. Лейпольд собрал в своей энциклопедии, девизом которой были слова «Сила без знания беспомощна», сведения практически обо всех машинах и инструментах, известных к 20-м годам XVIII столетия. Сочинения Лейпольда были написаны не общепринятой в ученом мире латынью, а по-немецки и поэтому оказались доступными для понимания не только университетским профессорам, но и простым ремесленникам. Долгие годы эти книги служили учебниками и справочниками как для начинающих, так и для опытных изобретателей и механиков. Известно, например, что великий Уатт специально изучил немецкий язык, чтобы познакомиться с описанными Лейпольдом паровыми машинами.

«Theatrum machinarium» — настоящий гимн профессии механика, который неплохо бы знать и помнить нынешним студентам механических факультетов.

«Механик... должен быть человеком, который не только знает подлежащие обработке материалы, такие, как дерево, сталь, железо, медь, серебро, золото, стекло и другие, и который умеет на основании физических законов решить, насколько каждый из этих материалов по своей природе и свойствам способен выдержать обработку, придающую необходимые пропорции и прочность... но он также должен выполнить свою работу в соответствии с механическими науками и с учетом требуемых размеров и существующих или предполагаемых нагрузок, для чего ему необходимо знать из геометрии и арифметики все то, что потребуется при расчете машины. И если он действительно хочет знать свое дело, он должен в совершенстве понимать все ремесла и науки, для которых ему придется изобретать и изготовлять машины, иначе он не сможет ничего усовершенствовать или изобрести что-нибудь новое, а именно это в первую очередь требуется от механика. Но, кроме того, он должен родиться механиком, чтобы не только быть искусным от природы в изобретательстве, но и уметь перенять все науки и ремесла таким образом, что о нем можно было бы сказать: то, что видят его глаза, могут сделать его руки. Его любовь к своей профессии не позволяет ему обойтись без тревог и расходов, ибо в течение всей жизни ему придется каждодневно учиться чему-нибудь новому и экспериментировать».

Одна из книг энциклопедии — «Theatrum arithmeticogeometricum», вышедшая в 1727 г. и полностью посвященная инструментальным средствам вычисления, может рассматриваться как первая в мире монография по вычислительной технике. В ней среди многих вычислительных устройств и машин Лейпольд описал несколько собственных изобретений.

Счетная машина Лейпольда (рис. 1) помимо круглой конструкции имеет еще одно отличие от известных арифмометров: ее работа основана на предложенном автором принципе так называемого «переменного пути зубчатки». Здесь в начале движения приводной ручки машины зубья зубчатой рейки сцеплялись с колесом основного счетчика и поворачивали его на определенный угол, а момент расцепления определялся путем, который проходил по ступенчатой пластинке специальный кулачок, связанный с устройством ввода.

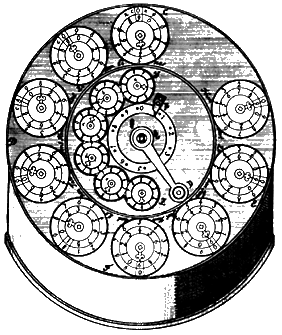
Рис. 1. Арифмометр Лейпольда

Для представления результата умножения в машине использовалось девять неподвижных цифровых дисков, расположенных во внешнем кольце СDFE и соответствующих единицам, десяткам, сотням и т. д. (Диски имеют две противоположные градуировки: одна для сложения и умножения, другая для вычитания и деления.) Поверх дисков скользят стрелкиуказатели, укрепленные на осях, проходящих через центры дисков. На тех же осях, но внутри машины, располагаются десятизубые храповые колеса G, H, I и т. д. Они приводятся во вращение девятизубой секторной рейкой NO (рис. 2, фиг. III), которая может поворачиваться вокруг оси W, укрепленной в зубчатом кольце РR. На рейке NО под прямым углом к ней укреплена тонкая пластинка х, показанная отдельно (рис. 2, фиг. IV). Левый боковой торец пластины плоский, правый выполнен в виде девяти ступенек равной высоты.

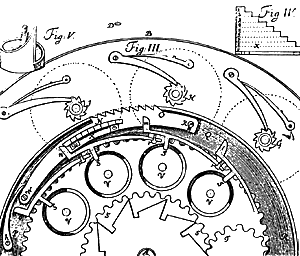
Рис. 2. Счетный механизм арифмометра Лейпольда

При вращении приводной ручки зубчатое кольцо РR вместе с рейкой NО поворачивается относительно внешнего кольца. Один из кулачков (l, т, п и т. д.), расположенный на свободном конце рычага, наталкивается своим закругленным торцом на пластинку x и, скользя по ее грани, перпендикулярной поверхности рейки, отжимает последнюю вверх, вводя ее зубья в зацепление с тем храповым колесом, мимо которого проходит рейка в данную часть оборота. Пройдя по боковой грани пластинки до конца ступеньки, кулачок проскакивает вперед по направлению к периферии машины, и рейка возвращается пружиной h в исходное состояние, выходя из зацепления с храповиком. Таким образом, число зубьев, на которое повернется одно из храповых колес (G, H, I), определяется длиной пути кулачка.

Для того чтобы произвольно менять длину этого пути, необходимо иметь средство для установки кулачка на различную относительно пластинки х высоту. Это достигается следующим образом: рычаг с кулачком, имеющий возможность поворачиваться в плоскости, перпендикулярной верхней крышке машины, несет на себе палец S, опирающийся на спиральную наклонную плоскость, показанную отдельно (рис. 2, фиг. V). При повороте оси v палец скользит по этой плоскости, поднимая конец рычага с кулачком и устанавливая его против определенной ступеньки пластинки х. Ось v оканчивается указателем, который поворачивается относительно одного из шести неподвижных цифровых дисков внутреннего кольца. Каждый диск лежит напротив диска внешнего кольца и используется для представления первого разряда множимого. Итак, во внешнем кольце машины располагается основной счетчик, а во внутреннем — устройство ввода. Сдвиг множимого осуществляется поворотом против часовой стрелки всей центральной части машины. Наконец, в центре машины размещен вспомогательный счетчик: его шкала видна на рис. 1, а храповое колесо — на рис. 2.

Механизм переноса десятков выполнен следующим образом.

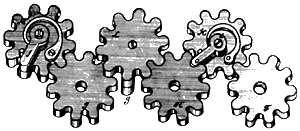
Рис. 3. Механизм переноса десятков в арифмометре Лейпольда

На осях основного счетчика расположены десятизубые колеса (G, H, I и т. д.), между которыми имеются промежуточные колеса К, L, M... (рис. 3, фиг. II). Каждое промежуточное колесо несет на себе подпружиненный палец (d, g, i...), причем у нечетных колес этот палец расположен над колесом, а у четных — под ним (рис. 3, фиг. I). При повороте на 360° колеса единиц G палец d поворачивает на 36° колесо десятков Н (расположенное выше, чем колеса G и К), благодаря чему совершается передача десятков. Аналогичным образом выполняется передача сотен, тысяч и т. д. 

Смерть помешала Лейпольду изготовить машину, и принцип «переменного пути зубчатки» был впервые реализован много позднее Дитцхольдом (1877) и Ф. Вайсом (1893).

Более удачливым оказался тишайший пастор Филипп Маттеус Ган. Именно ему мы обязаны созданием первого действующего арифмометра круглой формы — хитроумного устройства, внешне напоминающего ручную кофемолку.

Ган, родившийся 25 ноября 1739 г. в деревне Шарнхаузен близ Штутгарта, был одним из восьмерых детей викария местного прихода. В детстве он проявил склонность к живописи и астрономии. Найдя в библиотеке отца несколько астрономических руководств, он самостоятельно изучил их и мог точно определить время восхода и захода Солнца по положению звезд. Увлечение живописью привело Гана к тяжелому заболеванию: приготовляя краски и лаки, он отравился ядовитыми парами и долго болел.

В возрасте семнадцати лет Ган покинул родительский дом, чтобы изучать теологию в Тюбингенском университете, том самом университете, где сто с лишним лет назад учил богословие, а затем преподавал восточные языки и математику Вильгельм Шиккард — его славный предшественник на ниве механизации счета. Свой студенческий досуг Ган посвящал изучению математики и механики. Не имея средств для приобретения книг, Ган ночами переписывал их, а однажды, когда ему захотелось узнать устройство замысловатых часов, он на несколько месяцев обрек себя на хлеб и воду, пока не накопил сумму, необходимую для их покупки.

Вскоре Ган влюбился «в одну молодую особу, богатую и из хорошей семьи» и, желая получить ее руку, решил прославиться как знаменитый изобретатель. Урывая часы от сна и отдыха, он непрестанно конструирует то «инструмент для определения долготы в море», то «повозку, приводимую в движение паром», а то и... «вечный двигатель». Но все изобретения остались на бумаге из-за отсутствия средств для их изготовления. «И хотя,- как писал один биограф,- его труды не были вознаграждены успехом, на который он надеялся, он обязан этой страсти развитием благороднейших чувств и рождению той высокой репутации, которая соответствовала его таланту».

В начале 60-х годов Ган закончил университет и получил место викария небольшого прихода в деревушке Онстметтинген. Там несколько лет он работал над чертежами машины, воспроизводящей движение небесных тел. В 1764 г. местный механиксамоучка изготовил по ним деревянную «астрономическую машину»: движение часового механизма передавалось на диск, где Солнце, Луна и некоторые звезды «всходили» и «заходили» в течение всего года в строго определенное время; кроме того, Солнце и Луна проделывали свой путь по Зодиаку, и можно было наблюдать различные лунные фазы.

Вскоре Ган с помощью братьев и нескольких часовых подмастерьев сделал более точную «астрономическую машину», на этот раз металлическую, которую преподнес герцогу Вюртембергскому.

Слава Гана разнеслась по всей Германии. Его работами восхищался И.В. Гете, а писатель Лаватер отметил в своем «Физиогномическом фрагменте»: «...Исключительный выдающийся гений в механике, математике и астрономии. Он постоянно изобретает, беспрестанно творит, с огромным терпением, преодолевающим все трудности, выполняет все задуманное до конца. Он создает миры и простодушно рад своей спокойной творческой силе...».

Герцог Вюртембергский, покровительствовавший Гану, предложил ему занять место профессора и библиотекаря в Людвигсбурге, но тот предпочел остаться сельским священником.

В конце 60-х гг. Ган задумал новую «астрономическую машину», но внезапно прервал работу над ней и обратился к «счетным приборам». Впоследствии он писал: «Когда я был занят вычислениями над колесами астрономических часов, мне пришлось иметь дело с громаднейшими дробями и делать умножение и деление над весьма большими числами, от которых даже мои мысли останавливались, так что эта работа могла нанести ущерб моим прямым обязанностям. Тут я вспомнил, что когда-то читал о Лейбнице, что он занимался изобретением арифметической машины, на которую тратил много денег и времени, но удовлетворительного результата не достиг. У меня явилась мысль также поработать в этом направлении...»

В своем дневнике Ган указывает дату начала работы над машиной: «на Троицу 1770 года». Поначалу он попытался создать модель счетного механизма на два разряда. Получив удовлетворительный результат, он стал «наращивать» счетные возможности машины.

Ган не предвидел всей сложности работы. «Я должен был бы написать целую книгу,- отмечает он в дневнике,- чтобы рассказать о всех своих заботах и трудностях. Короче, я вскоре убедился, что все казалось ранее слишком легким и что машина будет готова через несколько недель... Однако, когда машина была готова до класса тысяч, открылись новые обстоятельства...»

Первые изделия, позднее уничтоженные автором, имели прямоугольные формы, но затем Ган перешел к машинам круглого вида. Уже в мае 1773 г. у него была вполне приемлемая небольшая модель счетной машины, и он приступил к строительству «действующего образца», о чем и записал 13 июля 1773 г. в дневнике. Ему помогали подмастерья местного часовщика, о которых Ган говорил: «Они... не имели природных данных и часто делали эту работу без охоты или вели беспорядочный образ жизни. Если я привлекал мастеров, они часто хотели быть умнее меня и были упрямы или работали слишком медленно, или требовали слишком большую плату».

Несмотря на все трудности, 11разрядная счетная машина была изготовлена уже в первые месяцы 1774 г., и Ган демонстрирует ее работу герцогу Вюртембергскому, а позднее удостаивается чести показать ее императору Иосифу II в герцогской библиотеке Людвигсбурга.

Однако изобретатель на этом не остановился и продолжил совершенствовать счетный механизм. В результате появилась четырнадцатиразрядная машина, завершенная в 1778 г. Уступая просьбам друзей, он подробно описал ее в журнале «Teutschen Mercur» в 1779 г.:

«Господин фон Лейбниц имел, по-видимому, веские основания сделать такие затраты* на подобные опыты. И если польза таковых окажется незначительной, поскольку при больших числах принято считать с помощью логарифмов, все же я удовлетворен, поскольку нашел то, что хотел, и могу использовать это, когда мне нужно, для самого себя. Верно, однако, что эта машина в мире единственная в своем роде. Если даже и существуют еще так называемые счетные машины, то я все же уверен, что нет такой совершенной и удобной, как эта».

Отличительной чертой машины Гана является, во-первых, круглая форма конструкции и, во-вторых, использование «ступенчатых валиков» Лейбница, которые изобретатель расположил вдоль боковой стороны машины. Каждый валик оканчивается стерженьком с десятью делениями, выступающими над верхней крышкой. Стерженьки (вместе с валиком) можно перемещать в вертикальном направлении на любое число делений от 0 до 9, устанавливая таким образом 12разрядное слагаемое (или множимое) в машине (рис. 4).

Рис. 4. Арифмометр Гана

Ступенчатые валики зацепляются с колесами основного счетчика, расположенными на 12 вертикальных осях. На каждой из них поверх крышки машины укреплена круглая эмалированная пластинка с двумя рядами (кольцами) цифр. Внешний ряд цифр (от 0 до 9) — черного цвета, внутренний ряд (от 9 до 0) — красного. Черные цифры используются при сложении и умножении, красные — при вычитании и делении. Пластинки располагаются по дуге, имея над собой плоскую стрелку с вырезом, через который видны считываемые цифры. За основным счетчиком размещены оси вспомогательного, чьи шкалы имеют один ряд цифр. Центральную часть машины занимает неподвижный круг с ручкой, делающей изобретение похожим на кофемолку, и стрелкойуказателем. Поворотом ручки число переносится с устройства ввода («ступенчатых валиков») на основной счетчик. При этом вспомогательный счетчик регистрирует число оборотов ручки. Сдвиг множимого осуществляется следующим образом: освобождают защелку, которая расположена на наружном крае машины, и поворачивают подвижное кольцо с основным и вспомогательным счетчиками до тех пор, пока стрелкауказатель не укажет нужный разряд вспомогательного счетчика; затем защелку закрывают и поворачивают ручку столько раз, сколько единиц стоит в соответствующем разряде множителя.

Круглую форму конструкции Ган мог заимствовать из лейпольдовской энциклопедии «Theatrum arithmeticogeometricum», в которой в самых общих чертах сообщается и о машине Лейбница. Однако совершенно не ясно, знал ли Ган о «ступенчатом валике» или пришел к этой мысли самостоятельно. Во всяком случае ни из книги Лейпольда, ни из других описаний лейбницевской машины он не мог почерпнуть сведений об этом элементе арифмометра.

Счетная машина Гана получила довольно широкую известность. О ней писали многие немецкие журналы, о ней был высокого мнения И.В. Гете, наблюдавший работу машины в доме профессора физики Готтфрида Христофора Бейерса, а писатель Жан Поль в своем «Палингенезине» задавался вопросом: «Почему не установили уже давно на земле машину Гана в качестве счетного ревизора, раз у нее есть совесть?».

Статья Гана в «Teutschen Mercur» побудила капитанинженера и строителя Иоганна Гельфрайха Мюллера из Дармштадта в 1783 г. сконструировать свою счетную машину и заказать ее изготовление часовому мастеру в Гиссене.

14разрядную машину Мюллера (рис. 5) отличали от машины Гана некоторые усовершенствования. Так, Мюллер заменил цифровые стержни, перемещавшиеся вверх и вниз по окружности машины, на вращающиеся диски с цифрами на боковой поверхности. Он также включил в механизм звоночек, подававший сигнал, если вычислитель допускал определенные ошибки (эту идею использовал позже в своей Аналитической машине «отец компьютера» Чарльз Бэббидж).

Рис. 5. Арифмометр Мюллера

Мюллер, избранный за создание счетной машины членомкорреспондентом Королевского геттингенского общества, опубликовал в 1784 г. ее подробное описание в «Геттингенском журнале ремесел и искусств», не удержавшись от нападок на Гана. Он заявлял, что машина последнего работает с ошибками, хотя и признал, что использовал многие идеи скромного священнослужителя.

В апрельском номере «Teutschen Mercur» за 1785 г. Ган выступил с умелой защитой своей машины. Он писал, что считал звонок в мюллеровской машине простой игрушкой, поскольку ошибки, которые обнаруживались благодаря звонку, видны и в его, Гана, машине. Надо только пользоваться глазами, а не ушами. Ган приводил высказывания авторитетных свидетелей в пользу точности работы его машины. «Если она (машина Мюллера. — Ю.П.),- пишет Ган,- совершает то, на что способна моя, то это в достаточной степени свидетельствует о познаниях господина Мюллера в механике, хотя он и располагал лучшим руководством в виде описания моего изобретения, чем то, которое было у меня,- описанием машины господина Лейбница». И высказав предположение, что Мюллер мог получить соответствующие указания от его, Гана, рабочих или от ученых, имевших доступ к его машине, добавляет: «Это, однако, не умаляет того, что у него (Мюллера. — Ю.П.) имеются большие способности, и я не буду спорить с ним о преимуществах моей машины, поскольку это и мне принесет мало пользы».

В защиту Гана (уже после смерти изобретателя) выступил издатель, экономист и статистик Христофор Фридрих Николаи. Он, ссылаясь на рассуждения о машине Мюллера, помещенные в одном берлинском журнале, писал: «Рецензента обманули, сообщив ему, будто машина Гана считает неверно. Это уже по одному тому маловероятно, что покойный Ган был не только крайне аккуратным, но и весьма честным человеком. Он никогда не приписал бы своему творению возможностей больших, чем те, которыми оно в действительности обладало».

Изготовленный в 1778 г. арифмометр был последней работой Гана в области счетной техники. Затем он вновь обратился к часовым механизмам и астрономическим приборам, «трудясь с привычным жаром, пока 2 мая 1790 года его не настигла смерть».

«Сегодня в Эхтердинге хоронят человека, который был гордостью Вюртенберга и славой Германии. Это Филипп Маттеус Ган, тамошний священник,- писал в своей “Хронике” поэт, органист и публицист Шубарт.- Величие его ума доказывают его изобретения в области механики, ни одно из них не было подражанием... Будь он британцем, его имя гремело бы по всему миру. Но он был лишь смиренным швабом, и открытия его ума были спрятаны под пеленой строжайшей скромности. Он был великим механиком...»

Из цикла статей напечатанных в журнале “Подводная лодка”, опубликованных в 1998-1999 году.
Статья опубликована в журнале “Подводная лодка” № 11, 1998 г.
Перепечатывается с разрешения автора

Статья помещена в музей 20.06.2008 года