Машина мятежного профессора

Юрий Полунов

7 мая 1673 года «куратор экспериментов» Лондонского королевского общества Роберт Гук выступил перед членами общества с докладом о способах механизации счетных операций. Со свойственной ему проницательностью Гук верно подметил те недостатки суммирующих машин, с которыми на протяжении двух следующих столетий с разной степенью успеха будут бороться изобретатели, и пришел к заключению о превосходстве письменного способа вычислений над машинным.

«Лучший способ сложения и вычитания заключается в записи чисел на бумаге и выполнении над ними действий обычной арифметики; обе части операции выполняются при этом быстрее и значительно надежнее, чем с помощью какого-либо инструмента; во-первых, запись чисел на бумаге требует вполовину меньше времени, чем при установке их на любом из известных инструментов; во-вторых, числа, постоянно оставаясь в поле зрения, могут быть быстро сложены и вычтены, а их сумма или остаток записаны; если же при вычислениях будет допущена какая-то ошибка, то их сейчас же можно будет повторить, что займет не более четверти усилий, которые тратятся на выполнение всей операции, в то время как при использовании инструмента для проверки результата потребуется повторить всю операцию полностью (т. е. установить числа и выполнить вычисления); человек в большей степени подвержен ошибкам при установке чисел посредством ключей, чем при записи цифр, выражающих это число. Следовательно, для облегчения выполнения этих арифметических операций инструмент не имеет большого значения, так как в лучшем случае он сокращает время обычного счета».

Примерно через полвека некоторые из названных Гуком недостатков счетных машин попытался преодолеть другой член Лондонского королевского общества немецкий математик, физик и астроном Христиан Людвиг Герстен.

О жизни этого ученого известно немногое. Он родился в феврале 1701 года в Гессене, главном городе графства Гессен-Дармштадт. 32 лет от роду он был назначен профессором Гессенского университета, но вскоре вынужден был оставить должность и родные края: будучи втянутым в судебный процесс, он потерял не только большую часть своего состояния, но и лишился значительной части профессорского жалованья, и поэтому решил поискать счастья в других краях. Он пытался найти работу в различных университетах Европы, добрался даже до Санкт-Петербурга. Но все его попытки оказались неудачными; вероятно, причиной тому был упрямый и вспыльчивый характер ученого. Герстен вынужден был вернуться на родину. Доведенный нуждою до отчаяния, он пишет в 1748 году ландграфу столь резкое письмо, что оскорбленный правитель приказывает посадить экс-профессора под домашний арест в один из замков Марксбурга. Здесь Герстен безвыездно живет около двенадцати лет, занимаясь математикой, астрономией, физикой и время от времени публикуя свои труды. Эти публикации приносят Герстену определенную известность в научных кругах Европы; его избирают членом Лондонского Королевского общества.

В 1760 году ландграф освобождает Герстена из-под ареста, определив ему местожительство в Браубахе, где он должен был неотлучно находиться еще в течение года (испытательный срок!). Однако мятежный профессор нарушил приказ и бежал во Франкфурт. Здесь в крайней бедности он умер 13 августа 1762 года.

Наибольшую славу Христиану Людвигу Герстену принесла его арифметическая машина, которую он изобрел в 1723 году, а изготовил двумя годами позднее.

В статье, опубликованной в 1735 году в «Философских трудах Королевского общества», Герстен так пишет об истории своего изобретения: «Первый толчок к рассуждению дала мне заметка Лейбница, которая заставила меня размышлять над тем, каким образом могло быть сконструировано внутреннее устройство машины. Но я был не в состоянии следовать идеям великого человека*, и поэтому собственные исследования сущности арифметических операций привели меня, в конце концов, к другой конструкции, которую я воплотил в грубой деревянной модели. Я показал ее нескольким покровителям и друзьям, которые посоветовали мне сделать медную модель машины. Но из-за отсутствия мастера, который бы смог воплотить мои идеи, мне пришлось отложить ее изготовление до 1725 года, когда, имея свободное время, я сделал модель для вычислений с семиразрядными числами».

Для того чтобы разобраться в устройстве и принципе действия этой одной из самых сложных суммирующих машин, воспользуемся несколькими рисунками, заимствованными из упомянутой статьи.

На рис. 1 показаны только три младших разряда, обозначенных АА, ВВ, СС, причем разряд единиц АА изображен без верхней крышки и некоторых внешних деталей.

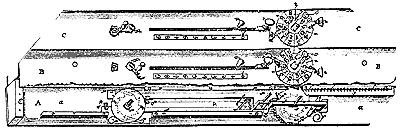
Рис. 1. Три младших разряда АА, ВВ, СС счётной машины Герстена

Механизм каждого разряда содержит две подвижные линейки, храповые и зубчатые колеса и монтируется на медном основании aaa. Первая подвижная линейка ggg, названная автором Оператором, движется в медных боковых желобах iii и qqq. В ее верхней части имеется ряд неподвижных стальных штырьков, а в центре находится выступ D, на котором крепится плата h со штырем. На штырь надевается ручка z, с помощью которой можно перемещать Оператор в желобках.

Вторая подвижная линейка – Определитель (kkk) – скользит в желобках ss и u. В ее верхней части имеется устройство, названное автором «замком» (рис. 2) и предназначенное для фиксации положения Определителя.

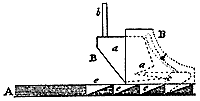
Рис. 2. "Замок" определителя

Делается это следующим образом. В основании aaa нарезано 10 зубьев еее. С ними в зацеплении находится собачка с, поджатая пружиной d. К «ключу» аa замка приварен штырь b, на который насаживается ручка ll. Нажимая на ручку, можно вывести собачку из зацепления и затем сместить Определитель вдоль машины. Его положение определяет расстояние, на которое Оператор может быть сдвинут влево. Если сместить Определитель так, чтобы собачка оказалась в зацеплении с i-м зубом, то Оператор можно будет сдвинуть влево на шаг i – 1.

В правой части машины в каждом разряде находится механизм, представляющий собой «сэндвич», который состоит из двух храповых и одного зубчатого колеса (см. рис. 1). Сверху находится десятизубое храповое колесо а с собачкой r, поджатой пружиной t. Под ним располагается второе храповое колесо b той же формы, но меньших размеров. Колеса а и b прикреплены друг к другу и имеют одну и ту же ось вращения. Под колесом b находится зубчатое колесо f, число зубьев которого (20 или более) равно числу штырей Оператора. Колесо f больше в диаметре, чем нижнее храповое колесо, но меньше, чем верхнее. На нем крепится подпружиненная собачка с, которая входит в зацепление с зубьями колеса b. Колеса «сэндвича» имеют общую ось вращения, установленную в мостике е-е.

Непосредственно под «сэндвичем» располагается Оператор, стальные штырьки которого при его смещении вдоль машины входят в зацепление с зубьями колеса f и поворачивают его в ту или иную сторону. Геометрические параметры колес «сэндвича» и шаг зубьев в основании aaa подбираются таким образом, что при перемещении Оператора на расстояние, скажем, равное трем шагам, колесо f поворачивается на такой угол, при котором собачка с проскальзывает по трем зубьям храпового колеса b.

В нижней части каждого разрядного механизма имеется еще одно храповое колесо mm, необходимое при выполнении операций умножения и деления. На этом колесе сверху укреплен круглый диск l с выгравированными по его периферии цифрами 0, 1, ... , 9. Ось, на которой вращается колесо с диском, крепится в основании машины. Храповое колесо располагается непосредственно над Определителем и имеет подпружиненную собачку n. Кроме того, в нижней части Оператора имеется еще одна подпружиненная собачка o, укрепленная на небольшом рычаге таким образом, что при каждом смещении Оператора вниз либо вверх вдоль машины она поворачивает колесо mm на один зуб.

Механизм «передачи десятков» выполнен следующим образом. К верхнему храповому колесу «сэндвича» приклепан стальной зуб таким образом, что один раз в течение полного поворота этого колеса он входит в зацепление с храповым колесом старшего разряда и поворачивает его на 1/10 оборота (рис. 3). Такое конструктивное решение требует, чтобы весь механизм старшего разряда был приподнят (на толщину передающего зуба) относительно младшего. Необходимо также, чтобы зубья храповиков смежных разрядов были нарезаны в противоположных направлениях. Соответственно этому и «сэндвичи» смежных разрядов будут вращаться в разные стороны.

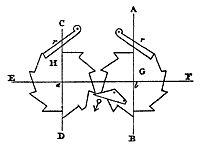
Рис. 3. Механизм передачи десятков

Весь разрядный механизм закрывается крышкой, которая крепится к боковым стойкам СС. На крышке имеется узкая прорезь, в которой перемещаются ручки Оператора и Определителя. Параллельно прорези нанесена шкала, интервал между делениями которой соответствует шагу нарезки зубьев в основании машины. Вдоль шкалы движется Указатель, укрепленный на боковой стойке Определителя и позволяющий установить последний в нужное положение. Кроме того, на крышке имеется окошечко, в котором видны цифры, выгравированные на диске l. Для установки храповика mm в нулевое положение на его ось, выступающую поверх крышки, наворачивается шайба ff с ручкой. На оси «сэндвича» крепится поверх посеребренный круглый диск x и ручка s. На плате имеется два концентрических кольца с десятью выгравированными на них цифрами 0, 1, ... , 9. Внешнее кольцо используется при сложении, внутреннее — при вычитании.

Диск поворачивается ручкой fs так, чтобы против Указателя w установилась нужная цифра внешнего кольца, а против Указателя y – внутреннего. Указатели выполнены в виде выпуклых стрелок. Это сделано для того, чтобы облегчить работу с машиной: диски соседних разрядов должны вращаться в разные стороны, соответственно направлению выпуклости указателей (нечетные разряды вращаются по часовой стрелке, четные – против). При изготовлении машины градуировку дисков выполняли следующим образом: «сэндвич» поворачивали до положения, при котором зуб передачи десятков касался храпового колеса старшего разряда. Тогда на диске против указателя w во внешнем кольце наносили цифру 9, а на внутреннем – против указателя y – цифру 0. Затем оба кольца делили на 10 равных частей. Далее во внешнем кольце нечетного разряда после цифры 9 гравировали в направлении против часовой стрелки цифры 0, 1, ... , 8, а во внутреннем – в том же направлении – после цифры 0 гравировали 9, 8, ... , 1. На дисках четных разрядов градуировка имела обратное направление. Цифры, находящиеся на одном и том же диске против указателей w и y, всегда составляли в сумме 9. При градуировке дисков l цифры на них наносили в том же направлении, что и на внешнем кольце диска x данного разряда.

Параллельно прорези, в которой движутся Оператор и Определитель, на крышке машины крепились пластины из слоновой кости, на которые записывались исходные данные вычислений.

При выполнении операции сложения цифры первого слагаемого устанавливаются в каждом разряде машины поворотом ручек fs в соответствующем направлении. Затем Определители ставят в положения, соответствующие цифрам второго слагаемого, и последовательно, начиная с 1-го разряда, смещают Операторы влево (до упора с Определителями) и вправо, в исходное положение. При движении Оператора влево его штыри поворачивают зубчатое колесо f и укрепленная на нем собачка с скользит по зубьям храповика b, причем число зубьев, по которым проходит собачка, равняется цифре в данном разряде второго слагаемого. При движении Оператора вправо та же собачка вместе с колесом f, вращаясь в противоположную сторону, поворачивает на такое же число зубьев храповики a и b, а вместе с ними – посеребренный диск x. Результат операции считывается с дисков против указателей.

Операция вычитания выполняется аналогичным образом, с той лишь разницей, что цифру уменьшаемого устанавливают на внутреннем кольце, напротив указателей y.

Рис. 4. Машина Герстена

Умножение осуществляется путем последовательного сложения множимого. Поворотом ручек fs и ff диcки x и l становятся в нулевое положение, а Определители – в положения, соответствующие цифрам множимого. Операторы смещают столько раз, сколько единиц в младшем разряде множителя. Число этих смещений регистрируется поворотом дисков и наблюдается в окошках. Затем снова устанавливают разрядные Определители, причем «единицы» множимого устанавливают в разряде «десятков», «десятки» – в разряде «сотен» и т. д., а Операторы вновь смещают столько раз, сколько единиц стоит в разряде десятков множителя и т. д.

Операция деления выполняется аналогичным образом. Цифры делимого устанавливают на внутренних кольцах напротив указателей y, и деление выполняется как последовательное вычитание делителя из делимого. Число этих вычитаний (частное) регистрируется при смещении Определителя каждого из них поворотом дисков l, а остаток считывается с дисков x против указателей y. Внешний вид машины показан на рис. 4.

Машина Герстена замечательна во многих отношениях: в ней впервые применено устройство для подсчета частного и числа последовательных операций сложения, необходимых при умножении чисел, а также (главное!) предусмотрена возможность контроля за правильностью ввода (установки) второго слагаемого, что снижает вероятность субъективной ошибки, связанной с утомлением вычислителя.

Из цикла статей напечатанных в журнале “Подводная лодка”, опубликованных в 1998-1999 году.
Статья опубликована в журнале “Подводная лодка” № 4, 1998 г.
Перепечатывается с разрешения автора

Статья помещена в музей 29.04.2008 года