Непер - na peer!

Юрий Полунов

Я всегда старался, насколько позволяли мои силы
и способности, избавиться от трудности и скуки
вычислений, докучливость которых обыкновенно
отпугивает очень многих от изучения математики.

Джон Непер

… Враги яростно наступали и теснили шотландцев до тех пор, пока королевское войско под предводительством Давида II (1329-1371) не обратилось в бегство. Тогда юный граф Дональд Леннокс выхватил знамя из рук знаменосца и храбро встретил врага. Удача изменила неприятелю, и шотландцы одержали крупную победу. После битвы король сказал, что все воины сражались храбро, но Дональд — Na peer (не имеющий равных). В знак благодарности за достойную службу король велел изменить фамилию героя и впредь именовать его Непером. Знал бы Давид II, что много столетий спустя английский историк адресовал почти те же слова потомку графа Леннокса, сказав, что Джон Непер «заслуживает звание Великого Человека более, чем любой другой шотландец, когда-либо появившийся на свет». И как бы, наверное, удивился король, узнав, что эта высочайшая похвала дана не за ратные подвиги, а за мирные труды на неведомом ему поприще математики!

… 450 лет назад город Эдинбург состоял из одной улицы длиною в милю, постепенно поднимавшейся от ворот Холирудского аббатства — резиденции шотландских королей — до Эдинбургского замка, возведенного на мрачных и неприступных скалах. Маленькие, грязные узкие боковые улочки сбегались к «королевской миле», беря начало прямо в полях и поросших вереском торфяниках. Подступы к городу защищали замки: на юговостоке возвышался величественный Крейгмиллар, на юго-западе одиноко стоял сравнительно небольшой Мерчистон. Замок имел в плане L-образную форму. Фронтальная (южная) его сторона длиной 43 фута была обращена к дороге, западная, имевшая 45 футов в длину, выходила в сад; с востока к замку примыкала площадка для игры в мяч, с севера — бассейн, источник воды для обитателей Мерчистона. По главной винтовой лестнице можно было попасть на любой из четырех этажей здания. Лестница заканчивалась в башенке, откуда был выход на зубчатую стену. Другая лестница вела из кухни в вырубленное в скале подземелье, где хранились пищевые запасы. Владельцем Мэрчистона был отец великого математика — лэрд (шотландский барон) Арчибалд Непер, помощник судьи и управляющий королевским монетным двором.

Род Неперов принадлежал к числу тех воинственных шотландских кланов, «этой эгоистичной, свирепой и беспринципной стаи гиен» (Т. Карлейль), которые всю жизнь воевали: друг против друга, против своих или чужих королей, вечно сбиваясь в шайки и клики. Совершенно необъяснимо, как в этой среде грубых и невежественных баронов, привыкших использовать пять пальцев руки для крепкого кулака, а отнюдь не для счета, появился великий математик!

Джаннет и Арчибальду Неперам не было еще и шестнадцати, когда в конце 1550 г. родился их первенец. Нелюдимый и замкнутый, слабого здоровья мальчик до тринадцати лет воспитывался дома, а затем был зачислен в один из колледжей университета Св. Андрея, где в течение примерно двух лет изучал грамматику, логику, теологию, каноническое и гражданское право, а также этику, физику и математику. Университет он не закончил, но продолжил образование на континенте, побывав во Франции, Италии и Дании. Вернувшись в Шотландию, Джон в феврале 1572 г. женился на дочери богатого землевладельца Элизабет Стирлинг. Молодые поселились в Гартнесе, в двадцати милях от Глазго, где на берегу полноводного Эндрика для них был выстроен просторный дом с садом и оранжереей. В Гартнесе Непер прожил без малого 35 лет. Здесь у него родились сын и дочь, здесь в конце 1579 г. умерла Элизабет, и спустя несколько лет Джон женился на ее троюродной сестре Агнесс (этот брак принес семье Неперов пятерых дочерей и пятерых сыновей).

В Гартнесе Непер вел жизнь «сельского джентльмена» и все свободное от присмотра за обширными земельными угодьями время отдавал занятию наукой — подозрительному и предосудительному, с точки зрения окружающих, делу. «Он имел привычку часто разгуливать в ночном халате и колпаке,- вспоминал современник. — Это наряду с некоторыми другими вещами, казавшимися простонародью довольно странными, утвердило за ним репутацию колдуна. Существовало мнение, что у него договор с дьяволом и что под предлогом занятий наукой он проводил время в изучении черной магии и беседах со Старым Ником» (так в Шотландии называют черта. — Ю.П.).

Джон Непер не пытался разуверить окружающих, а напротив, своеобразно использовал эту убежденность. Однажды у него дома случилась пропажа. Подозрение пало на слуг, но ни одного из них нельзя было обвинить наверняка. И тогда Непер объявил, что его черный петух обладает способностью открывать своему хозяину тайные мысли. Каждый слуга должен был войти в темную комнату, где находился петух, и дотронуться до него рукой. Было сказано, что петух закричит, когда вор до него дотронется. И хотя петух так и не закричал, Непер все же определил вора: он предварительно обсыпал петуха золой, и чистые пальцы одного из слуг стали доказательством его виновности.

Надо думать, что и сам Непер верил в существование сверхъестественных сил. Сохранился любопытный документ — договор, согласно которому Непер брался, используя свое необычайное искусство заклинаний, открыть местонахождение клада в одном из старых и мрачных шотландских замков. «Рожденный в век, когда не признавать ведьм значило в глазах людей то же самое, что оправдывать их нечистые деяния, Домини сжился с этими легендами и верил в них так же свято, как верил в бога»,- писал об учителе Сэмсоне в «Гае Мэннеринге» другой великий шотландец — Вальтер Скотт. Эти слова, пожалуй, как нельзя лучше относятся и к Джону Неперу.

Увлекался Непер алхимией и астрологией, следствием чего явился опубликованный уже после его смерти «Кровавый альманах, содержащий много верных предсказаний относительно того, что произойдет в текущем 1647 году. Вместе с вычислениями дня Страшного суда составлен и опубликован знаменитым астрологом лордом Непером Мэрчистонским».

Но, видимо, с особым удовольствием Непер — владелец обширных угодий — занимался вопросами сельского хозяйства. Он пытался повысить урожайность хлебов, удобряя землю солью, изобрел несколько полезных сельскохозяйственных орудий, таких, как гидравлический насос, облегчающий поливку сада.

Впрочем, Непер изобретал орудия и пострашней: в 1596 г., когда опасность испанской интервенции была еще велика, он направил, говоря современным языком, докладную записку одному из придворных короля Иакова VI Шотландского: «Секретные изобретения, полезные и необходимые в наши дни для защиты Острова и борьбы с иноземцами, врагами божьей веры и религии».

«Секретные изобретения» включали:
зеркало для сжигания вражеских кораблей на любом заданном расстоянии;
устройство для плавания под водой с ныряльщиками, различными приспособлениями и военными хитростями для нанесения вреда врагу;
круглую колесницу, непробиваемую выстрелами из сдвоенного мушкета и движимую теми, кто находится внутри;
и, наконец, орудие, при выстреле из которого ядра летят не по прямой линии, поражая, как у других, лишь то, что случайно окажется на его пути, но движется, рыская, над поверхностью целого заданного района и не покидает его до тех пор, пока не израсходует свою силу.

«Врагами» для Непера, страстного приверженца протестантизма, были католики, паписты, которые всячески стремились вернуть Шотландию в лоно католической церкви. Для разоблачения «наглых идолопоклонников» Непер написал и в 1593 г. издал на английском языке книгу «Простое объяснение всех откровений Св. Иоанна», которая интересна для нас тем, что позволяет еще более приблизиться к личности великого математика.

Публикуя свои комментарии к апокалипсическим пророчествам святого, Непер преследовал две, тесно связанные между собой цели: теологическая цель состояла в том, чтобы показать антихристианский характер католической церкви, политическая цель заключалась в том, чтобы изменить отношение короля к делу установления новой религии.

В письме Иакову VI, предшествующем посланию книги, Непер писал: «… Сэр, пусть постоянным занятием Вашего величества… будет искоренение всеобщих гнусностей в вашей стране и… прежде всего в собственном доме, семье и дворе и очищение их ото всех подозрений в папизме, атеизме или предательстве. Ибо может ли быть государь… избавителем мира от антихристианизма, если он не очистил от него свою собственную страну? Очистит ли страну тот, кто не очистил свой дом? Или очистит ли свой дом тот, кто не очистился сам через созерцание своего Бога?»

Подобные поучения свидетельствуют — в условиях вероятной контрреформации — о несомненной смелости Непера.

В книге Непер с помощью числовой мистики расшифровывал апокалипсические пророчества, доказывая, что десятирогий зверь из бездны — Римская империя; Антихрист — римский папа, который одновременно является и Гогом, в то время как Магогом следует считать турков и других магометан; что Страшный суд наступит между 1688 и 1700 гг. и т. д.

Любопытно, что книга заканчивается «Пророчеством Сивиллы», заимствованным из латинского текста Кастальо, но представленным автором своему английскому читателю десятью страницами терцин: по-видимому, Непер, как, впрочем, многие homo universalis того времени, был не лишен стихотворного дара. Об этом свидетельствует и возвышенный, поэтический, хотя и несколько цветистый — в традициях времени — язык, которым написана книга. Вот, например, какими словами завершается предисловие к ней:

«… Я уверен, что по стилю и выражениям мой язык ужасающе груб, и в этом отношении я ставлю себя ниже кого-либо другого; вряд ли я даже по зрелому размышлению мог бы найти слова, чтобы выразить свои мысли об этом высоком предмете… Но видя эти недостатки, Господь, быть может, обратит их в великое достоинство скромности и сломит тщеславие… И коль скоро наше доброе намерение и благочестивая цель воистину исходят из очень нежного и хрупкого сосуда, и так же, как все жидкости (как бы драгоценны они ни были), заимствуют часть вкуса от содержащих их сосудов, так и этот праведный труд может в некоторых вещах (хотя и незамеченных мною) иметь привкус моих недостатков. Поэтому смиренно представляю я эти несовершенства для великодушного исправления каждому благоразумному и мудрому человеку, кто о движении господнего духа судит честно, но без зависти и пристрастия, и молю всех добрых людей простить меня за все, что написано неверно; ибо хотя я сделал это не настолько совершенно, насколько должен был сделать, зато так усердно, как только мог, зная, что скромная лепта бедной вдовицы будет угодна богу; ибо не у всякого человека есть золото, серебро, шелка и пурпур, чтобы предложить их для святилища; но мне (как говорит Иеремия) уже много, если я смогу купить шерсть или очески и отдать их для священных деяний».

Для нас представляются достойными гения Непера лишь его математические работы. Он занимался наукой исключительно ради удовлетворения прирожденной жажды знаний и неохотно отдавал свои труды в распоряжение печатного станка. По этой причине первое математическое сочинение Непера «De arte logistica», посвященное некоторым вопросам арифметики и алгебры, вышло в свет лишь в 1839 г.; хотя заметки, из которых оно составлено, можно отнести к 70-м годам XVI в., а знаменитый трактат «Описание удивительных таблиц логарифмов» был издан только в 1614 г., примерно через 20 лет после того, как Непер пришел к идее логарифмических вычислений и подготовил первый вариант своих таблиц.

Трудно назвать другое сочинение, совершившее столь же глубокий переворот в прикладной математике. Сведение сложных операций к более простым осталось непревзойденным средством упрощения вычислений в течение последующих столетий. Перефразируя Норберта Винера, можно сказать, что если бы наука вычислений нуждалась в святом покровителе, то им следовало бы назвать Джона Непера.

Современники Непера высоко оценили значение его изобретения, столь отвечающего потребностям времени. Достойным преемником шотландского математика в Англии стал профессор лондонского Грэшем-колледжа Генри Бригс. Его биограф так описывал энтузиазм, с которым 54-летний ученый встретил появление «Описания…»: «Он берег книгу как зеницу ока и постоянно носил с собой либо за пазухой, либо прижимал к сердцу… Жадными глазами, отрешенно, внимательно перечитывал ее снова и снова… Она была предметом его восхвалений в повседневных беседах с друзьями и на кафедре, он излагал ее содержание ученикам…»

Восхищение Бригса было не созерцательным, а активным, творческим. Хотя в книге Непера были приведены лишь таблицы логарифмов синусов, косинусов и тангенсов, он быстро сообразил, что с помощью «удивительного изобретения» могут быть вычислены и другие таблицы. Он попытался найти логарифмы целых чисел, степеней, корней и частных, но обнаружил, что Неперова система более приспособлена для тригонометрических функций. И тогда он вознамерился улучшить ее! «Своими новыми и удивительными логарифмами Непер, лорд Мерчистонский, заставил меня усиленно работать головой и руками; я надеюсь увидеть его летом, если будет угодно…» — писал Бригс архиепископу Джеймсу Ашеру.

Во время летних студенческих каникул Бригс отправился в Шотландию, чтобы отдать Неперу дань уважения и обсудить с ним возможные изменения в системе логарифмов. Сохранился любопытный рассказ об их первой встрече.

Вследствие задержки в пути Бригс не приехал в заранее назначенное время, и Непер пожаловался на это одному из своих друзей, математику Джону Марру. «Увы, Джон,- говорил он,- мистер Бригс не приедет. Но в тот же момент кто-то постучал в ворота, Джон Марр поспешил выйти, и, к великому своему удовольствию, увидел мистера Бригса. Он проводил его в комнату милорда. Около четверти часа Непер и Бригс восхищенно смотрели друг на друга, не говоря ни слова. Наконец мистер Бригс начал: «Милорд, я предпринял это долгое путешествие только для того, чтобы увидеть вас и узнать, с помощью каких глубин разума и изобретательности вы пришли впервые к мысли об этом превосходном пособии для астрономов, а именно о логарифмах, но милорд, после вашего открытия, я удивился, почему никто не нашел их раньше настолько легкими они кажутся…»

Бригс провел у Непера месяц. Мерчистонский барон познакомил нового друга с рукописью своей книги «Устройство удивительной таблицы логарифмов», в которой объяснял способ их вычисления и попросил отредактировать и подготовить ее к печати (что Бригс впоследствии и сделал). В беседах ученых родилась идея десятичных логарифмов, более совершенных, чем те, что поначалу предложил Непер. Лэрд Мерчистона, обремененный заботами о своем огромном семействе, жестоко страдающий от подагры — болезни, которая через несколько лет свела его в могилу,- уже не мог проделать огромный объем вычислений, необходимых для составления таблиц новых логарифмов. За эту задачу, вернувшись в Лондон, с жаром взялся Бригс. Вскоре, однако, ему пришлось на время отложить работу ради другой, не менее важной и благородной: подготовки к изданию английского перевода «Описаний…», выполненного Эдуардом Райтом, чьи труды занимают почетное место в истории навигационной науки.

Завершив труды по изданию перевода, появившегося на свет в 1616 г., Бригс вновь засел за вычисления таблиц десятичных логарифмов и летом 1616 г. отправился в Шотландию, чтобы показать первые результаты своего труда. Непер тем временем был занят подготовкой к печати своего последнего трактата — «Рабдология, или Две книги о счете с помощью палочек», в предисловии к которому писал: «Теперь мы также нашли значительно лучшую разновидность логарифмов и намерены (если бог дарует долгую жизнь и хорошее здоровье) опубликовать как метод их вычисления, так и способ использования. Но по причине нашей телесной слабости само вычисление этих новых таблиц мы предоставляем людям, опытным в такого рода занятиях, и, прежде всего, ученейшему мужу Генри Бригсу, профессору геометрии и нашему дражайшему другу».

Бригс обещал Неперу незамедлительно закончить вычисления таблиц и летом следующего года привезти их в Шотландию. Однако этой поездке не суждено было состояться: 4 апреля 1617 г. закончил свой земной путь мерчистонский барон, великий Na peer.

Можно смело сказать, что дружба и совместная работа с Бригсом озарили последние годы жизни великого математика. Их отношения — образец сотрудничества ученых, решающих одну и ту же проблему. Эти немолодые уже люди относились друг к другу с глубочайшим уважением и трогательным вниманием. Бригс постоянно подчеркивал, что является всего лишь учеником Непера и проводником его идей, а Непер, в свою очередь, высоко оценивал способности лондонского профессора в своих высказываниях.

Вероятно, Непер установил «иерархию» важности своих трудов, поэтому, когда его здоровье резко ухудшилось, он распорядился издать не «Устройство…», а «Рабдологию», которой он придавал в то время, по-видимому, большее значение. Книга вышла в Эдинбурге в начале 1617 года.

Термин «рабдология» Непер объяснял как «счет с помощью маленьких палочек»[1]. В предисловии к книге он писал, что изобрел их для тех, кто предпочитает логарифмам вычисления с «естественными числами»[2], и решился на публикацию потому, что «палочки» понравились многим его друзьям и даже были перевезены в другие страны.

Эти палочки, изготовленные из дерева или из слоновой кости, под названием «палочки (или кости) Непера», как и сам метод умножения с их помощью, быстро получили распространение в Европе и были одно время даже более популярны, чем логарифмы. «Рабдология» была вскоре переведена на итальянский, датский, французский языки и только в 1667 г. — на английский (под названием «Искусство счета с помощью говорящих палочек, обычно именуемых костями Непера»).

Непер наверняка знал о приеме умножения, описанном в известном средневековом трактате Луки Пачоли «Summa de arithmetica» под названием gelosia (этот прием задолго до Пачоли был знаком индийцам). Суть его в следующем.

Счетную доску (или просто лист чистой бумаги) расчерчивали в виде сетки прямоугольников, разделенных диагоналями. По сторонам сетки (сверху и справа) записывали сомножители, а промежуточные произведения помещали в прямоугольники так, чтобы диагональ разделяла единицы и десятки (единицы помещались в нижний треугольник, а десятки — в верхний). Для получения произведений осуществляли суммирование «вдоль диагоналей», а результат записывали внизу сетки (младшие разряды) и слева от сетки (старшие разряды)[3]. Непер предложил разрезать «школьную» таблицу умножения на 10 полосок (включая нулевую) и числа разделить диагональю на единицы и десятки. Пусть требуется умножить 2085 на 4 (рис. 1). Делали это так: брали палочки для цифр 2, 0, 8 и 5 и еще одну — единичную. Палочки прикладывали друг к другу так, как показано на рисунке, и против цифры 4 единичной палочки искали произведение 4 на цифры 2, 0, 8 и 5, из которых составлено множимое.

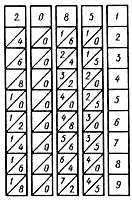
Рис. 1. Умножение на палочках Непера

Суммируя числа, как в gelosia, получаем: 2085 в 4 = 8; (0 + 3); (2 + 2); 0; = 8340.

Если множитель многозначный, то отдельные произведения выписывали, как обычно, со смещением на один разряд, а затем складывали. Для множимого, содержавшего несколько одинаковых цифр, приходилось иметь несколько одинаковых палочек. Поэтому Непер предложил выполнять палочки в виде прямоугольных параллелепипедов и наклеивать на них не одну, а 4 полоски (по одной на каждую грань) таким образом, чтобы первая палочка содержала полоски для 0, 1, 9, 8; вторая — для 0, 2, 9 и 7; третья — для 0, 3, 9 и 6 и т. д. вплоть до 10-й, содержавшей полоски для 3, 4, 6 и 5.

Таким образом, каждая палочка имела на противолежащих гранях полоски для некоторой цифры и ее дополнения до 9. С помощью «палочек Непера» можно было выполнять не только операцию умножения, но и деления и извлечения квадратного корня. Следует отметить, что содержание «Рабдологии» не ограничивается описанием «палочек». В книге автор подробно говорит еще об одном изобретении: «… раздумывая над тем, как облегчить тяжкий труд вычислителя, я пришел к идее некоторой табличной арифметики, с помощью которой наиболее трудоемкие арифметические операции выполняются на абаке или шахматной доске и которую можно рассматривать как развлечение, а не как труд; ибо с ее помощью сложение, вычитание, умножение, деление и даже извлечение квадратного корня выполняется простым движением жетона».

Речь идет о счетной доске, разделенной на квадраты, подобно шахматной и о правилах вычислений с ее помощью, основанных на использовании двоичной (!) системы счисления, что было первым практическим применением этой системы.

Завершая рассказ о изобретениях Джона Непера, уместно вспомнить слова одного знаменитого математика: «Для того, чтобы математическая теория была верна, она должна быть красива». Все изобретения Непера красивы, и, больше того, они, как все гениальное, просты и, на первый взгляд, очевидны (вспомним слова Бригса, сказанные им при первой встрече с Непером в Мерчистоне). А палочки? Ведь от таблицы умножения и метода gelosia до «палочек Непера» — один шаг! Но никто из математиков средневековья и Возрождения не обратил внимания на эту, казалось бы, очевидную возможность упрощения операции умножения, и этот единственный шаг был сделан Непером.

Наверное, ни одна идея в истории вычислительной техники не дала столько пищи изобретательным умам, как идея «палочек Непера». На протяжении трех веков было сделано множество улучшений и модификаций «палочек». Быть может, последней из них была брошюра «Настольная таблица умножения для сложных вычислений», вышедшая в Ленинграде в 1930 году! Сравнивая «быстроту чтения результата с работой на русских счетах», автор писал: «Преимущества на стороне таблицы, сохраняющей вам мышцы рук и шеи от лишних движений, а мозг — от лишней работы».

В 1892 г. француз Прюво ле Гюэ распространил идею Непера на двузначные числа. Его «счетные бруски» содержали произведения каждого из чисел (от 1 до 99) на 1, 2, … , 8, 9. На одной стороне бруска изображались произведения для четного числа, на другой — для следующего за ним нечетного (например, 12 и 13, 26 и 27 и т. д.). Бруски помещались в ящичке, и для удобства поиска на их верхних торцах писались четные числа, а на нижних — нечетные.

Но, пожалуй, наиболее остроумная модификация «палочек» была предложена в 1885 г. двумя французскими изобретателями: железнодорожным инженером Женейем и сотрудником парижского Музея искусств и ремесел Эдуардом Люка. Набор Женейя и Люка содержал 11 брусков. Один из них, соответствующий множителю, имел боковую грань, разделенную на два вертикальных столбца. Левый столбец был разбит на 8 клеток с цифрами 2, 3, … , 9, означающими множитель. Правый столбец разбивался на различное число клеток в зависимости от множителя: против множителя 2 были две клетки с цифрами 0, 1, против множителя 3 — три клетки с цифрами 0, 1, 2 и т. д. (рис. 2).

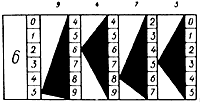
Рис. 2. Палочки Женейя — Люка

У остальных 10 брусков использовались все боковые грани. Каждая из них также разбивалась на два вертикальных столбца. В самом верху грани справа была написана цифра множимого. Далее правая колонка разбивалась так же, как и на бруске, описанном выше. Произведение однозначных чисел записывалось так: верхняя клетка правой колонки содержала цифру единиц произведения; в следующих клетках писались соседние цифры в порядке возрастания. Цифра десятков изображалась в левой колонке с помощью черного треугольника, вершина которого находилась на высоте нужной клетки. Благодаря этому, читая цифры результата против вершин, можно было избавиться от необходимости сложения для получения нужных значений разрядов.

Мы расстаемся с изобретениями достославного барона Непера ненадолго, поскольку в следующей статье познакомимся с попытками «механизации» его «палочек» и создания специализированных счетных множительных машин.

Примечания

1. Rabdos — палка, прут.

2. Непер иногда называл логарифмы numeri artificialis (искусственные числа) в противоположность numeri naturalis (естественные числа).

3. По мнению Пачоли, запись выкладок при этом методе напоминает решетчатые оконные ставни, скрывавшие от взоров прохожих сидящих у окон женщин. Такие ставни называли gelosia (жалюзи), что по-итальянски означает «ревность».

Из цикла статей напечатанных в журнале “Подводная лодка”, опубликованных в 1998-1999 году.
Статья опубликована в журнале “Подводная лодка” № 5, 1998 г.
Перепечатывается с разрешения автора

Статья помещена в музей 12.06.2008 года