Мирный снаряд из белостока

Юрий Полунов

У одного русского писателя есть рассказ о математике-самоучке из маленького еврейского местечка, который в XIX веке изобрел дифференциальное исчисление и умер от огорчения, узнав о том, что до него это уже сделали Ньютон и Лейбниц.

Судьба Хаима-Зелика Слонимского оказалась счастливее. Слонимского, родившегося 19 марта 1810 года в Белостоке, с детства готовили к религиозной карьере, поэтому начальное образование он получил в хедере – начальной школе, а затем в бет-гамидраше – молитвенном доме и школе для тех, кто посвятил себя изучению Талмуда. На семнадцатом году жизни он женился и переехал в местечко Заблудово близ Белостока в дом тестя, обязавшегося содержать его семью в течение трех лет, пока Слонимский будет совершенствоваться в изучении Талмуда.

Однажды совершенно случайно Хаим-Зелик купил у разъезжего книготорговца книгу некоего Рафаила Гановера под названием «Технут Гашомаим», т. е. «Описание неба, или Астрономия» (Амстердам, 1756). Он сразу же наткнулся на непонятные места в тексте книги, которые автор не объяснял, ссылаясь на незнакомые геометрические теоремы и аксиомы. Вскоре Слонимский узнал, что у соседа есть книга о еврейском календаре, в которой в качестве приложения сообщаются некоторые сведения по геометрии и тригонометрии. Ему удалось заполучить «драгоценную» книгу, но листы с чертежами оказались вырванными. Все же Хаим-Зелик смог по тексту восстановить чертежи и даже доказать некоторые теоремы по-своему.

Следующую книгу по астрономии – «Шевиле дерокиа» («Стези неба») – Слонимский взял «напрокат» у одного жителя Белостока и вернул ее спустя всего лишь две недели. Пораженный успехами юноши, владелец книги посоветовал ему немедленно заняться изучением немецкого языка. Он познакомил Слонимского с основными грамматическими правилами, а затем отпустил с «Алгеброй» Эйлера, которая должна была заменить Хаиму-Зелику и букварь, и хрестоматию. Вернувшись домой, Слонимский начинает по ночам, дабы не навлечь на себя гнев набожного тестя, учить и алгебру, и язык. На освоение уходит четыре недели.

По истечении трех лет Слонимский, который к этому времени уже стал отцом двоих детей, поступает на службу к брату, владевшему маленьким стекольным заводиком. Впрочем, через некоторое время предприятие «лопнуло», и Хаим-Зелик открыл собственную торговлю, которой в основном занималась его жена. Слонимский же, прошедший нелегкий «путь познания», уже определил к этому времени свое назначение в жизни – быть, говоря по-современному, пропагандистом научных знаний среди еврейской молодежи.

Но как сделать, чтобы всесильный Раввинат разрешил публикацию его будущих статей и книг? Ведь жители убогого местечка, запуганные и нищие, уже поговаривают, что зять достойного человека и большой знаток Талмуда читает богопротивные книги и утверждает – о ужас! – что Земля вращается вокруг Солнца. Что и говорить, задача стояла перед Слонимским нелегкая, но, как мы увидим, он блестяще с ней справился.

Слонимский пишет «Мосде Хохма» («Основа мудрости» – руководство по математике, от арифметики до интегрального исчисления). Сжатостью и формой изложения руководство напоминало Талмуд, и это ставило своей целью не оттолкнуть, а привлечь церковь. В 1834 году он приезжает в Вильно со своей книгой и получает благосклонные рецензии от тамошних раввинов. Однако денег на издание не хватило, и свет увидела только часть, касающаяся алгебры. С трудом компенсировав выручкой от продажи руководства затраты на его издание, без единого гроша возвращается Слонимский в Заблудово.

В следующем году ему представляется удобный повод для пропаганды научных знаний: в связи с появлением кометы Галлея среди населения города ходили слухи о близком Конце Света, и Слонимский решил выступить с сочинением, разъясняющим суть небесных явлений. Его новая книга называлась «Кохбе де Шабит» – «Звезда с хвостом». Уже одно ее название должно было привлечь еврейскую молодежь, получавшую, в основном, религиозное образование и поэтому наверняка помнившую слова рабби Самуила «Для меня ясны все стези на небе ... кроме пути хвостатой звезды, который мне не известен». У молодых людей, знакомых лишь с мертвой схоластикой Талмуда, название книги вызывало интерес и любопытство: что же можно сказать о «звезде с хвостом» помимо того, что сказал Учитель? Неужели современные астрономы превзошли его и умеют точно предсказывать появление и исчезновение загадочного небесного тела?

Книга Слонимского представляла собой по существу популярный очерк развития астрономии. Автор писал о Копернике, о трех законах Кеплера, о законе всемирного тяготения, об астрономических приборах, а в конце книги приводил сведения о кометах, условиях их появления, орбитах и т. д.

«Звезда с хвостом» имела большой успех и много раз переиздавалась, а автор ее был тем временем занят составлением новой книги, на этот раз популярного руководства по астрономии. В нем Слонимский решил привести, в частности, результаты своих собственных исследований, касающихся способов вычислений дат затмений и построения еврейского календаря, весьма запутанного и сложного. Для издания книги он едет в Варшаву, где знакомится с директором Варшавской обсерватории Фр. Арминским. Профессор Арминский не только написал предисловие к руководству (оно вышло в свет в 1838 году), но и ходатайствовал об освобождении Слонимского из-под ареста: дело в том, что каждый иногородний еврей должен был платить за день пребывания в Варшаве налог в 20 грошей, а у Слонимского даже таких денег не было, и он попал в каталажку...

Поездка в Варшаву имела большое значение для дальнейшей жизни Слонимского: здесь он познакомился с Авраамом Штерном, членом варшавского «Общества друзей науки», дочь которого в 1842 году стала женой Хаима-Зелика.

Штерн был известен как автор счетной машины, которую он демонстрировал в салоне князя Михаила Радзивилла самодержцу российскому Александру I. Ко времени появления Слонимского в доме Штерна тот задумал новую «числительную машину», но умер, не осуществив своего замысла.

Переезд Слонимского в Варшаву избавил его от мелочной опеки религиозных родственников и позволил полностью посвятить себя занятиям наукой. На правах наследника Штерна он решает закончить задуманную им счетную машину и некоторое время занимается ею, впрочем, без особого успеха.

Слонимский интересовался счетными машинами и ранее, вероятно, в связи с трудоемкими вычислениями, которые ему пришлось делать при работе над усовершенствованием еврейского календаря. В 1843 году, когда он отважился на поездку в Берлин, у него уже имелась оригинальная «числительная машина», предназначавшаяся для умножения и деления целых чисел и извлечения корней; машина основывалась на теореме теории чисел, сформулированной самим Слонимским.

В Берлине Слонимский знакомится со многими известными математиками, астрономами и естествоиспытателями. Свою машину он демонстрирует 12 августа 1844 года перед членами Берлинской академии и получает похвальные отзывы таких ученых, как Карл Якоби, Август Крелле, Фридрих Бессель.

Особое участие в судьбе Хаима-Зелика принял президент академии Александр Гумбольт, который был не только великим естествоиспытателем, но и, как мы сказали бы сегодня, борцом за права человека, самоотверженно выступавшим против рабства на Кубе, против крепостного права в Пруссии и России, против ограничения прав евреев. Желая поддержать молодого ученого, Гумбольт снабдил Слонимского письмом к прусскому королю Фридриху Вильгельму IV.

Из Берлина Слонимский направляется в Кенигсберг, где находился в то время король, и, продемонстрировав свою машину, получает некоторую сумму денег и рекомендательные письма в Петербург. Но перед тем как попасть в столицу Государства Российского, Слонимский вынужден был в ожидании паспортов несколько месяцев обивать пороги канцелярии наместника Царства Польского маршала Паскевича. Наконец он оказывается в Петербурге, где обращается со своими рекомендательными письмами к министру народного просвещения и президенту Академии наук С.С. Уварову. По предложению Уварова физико-математическое отделение Академии на своем заседании 4 апреля 1845 года заслушало Слонимского, демонстрировавшего прибор и пояснявшего его работу. Отделение поручило академику В. Я. Буняковскому и секретарю Академии П. Н. Фуссу рассмотреть это изобретение и дать о нем письменный отзыв.

Высоко оценивая работу Слонимского, рецензенты ходатайствовали о награждении его Демидовской премией[1]. «Мы убеждены,– говорилось в отзыве,– что этот молодой и скромный математик, известный уже и некоторыми другими своими трудами, в полной мере заслуживает поощрения. Первый успех на поприще математики будет тем живительнее для него, что он поставлен обстоятельствами в беспрерывную борьбу духа любознательности со строгою нуждою, отрывающею его на каждом шагу от занятий умственных».

Премия размером 2500 рублей была присуждена Слонимскому на чрезвычайном Демидовском собрании 17 апреля 1845 года, а еще через некоторое время в Петербурге вышла брошюра «Описание нового числительного инструмента Слонимского».

Помимо «числительного инструмента» Слонимский привез в Петербург более скромное изобретение, о котором в отзыве Фусса – Буняковского говорилось: «...кроме главного инструмента г-н Слонимский представил снаряд для сложения и вычитания, он очень прост и удобен на практике...»

Можно предположить, что «снаряд» был изобретен до «числительного инструмента» и именно об этом «снаряде» писал в № 60 от 26 июля 1840 года «Литовский вестник», выходивший в Вильно: «Еврей Х.З. Слонимский, белостокский уроженец, изобрел малую счетную машину, которая по своему объему... удобству и дешевизне заслуживает того, чтобы ввести ее в общее употребление. Каждый, кто знает цифры, с помощью этой машины может считать весьма удобно, скоро и безо всякого размышления. Эту машину можно видеть у изобретателя, который занимается изготовлением другой, изобретенной им же, машины для логарифмов. Посредством этой машины удобно и легко можно находить дифференциацию логарифмов Бригета (десятичных логарифмов Бригса. – Ю. П.), равно как и порядков до 14 десятичных знаков,– изобретение, которое еще первый раз является в кругу механизма математики. Математические и астрономические познания даровитого г-на Слонимского, а также его математические сочинения на еврейском языке... не дозволяют нам сомневаться в справедливости и важности его изобретения».

«Снаряд для сложения и вычитания» был суммирующей машиной, на которую 24 ноября 1845 года изобретатель получил патент. Машина имеет несколько 24-зубых колес одинакового диаметра, сделанных из тонких металлических пластинок. Колеса насажены на параллельные оси и вращаются с помощью ведущего штифта: для этого он вставляется в одно из отверстий, расположенных по окружности колеса. Часть этой окружности зачернена, и ближе к центру по дуге нанесены цифры 0, 1, 2, ... , 9 (рис. 1).

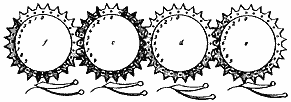
Рис. 1. Счетный механизм машины

Колеса вырезаны по окружности до половины своей толщины, так что та часть колеса, где написаны цифры, находится выше, нежели край того же колеса. Колеса расположены так, что своими вырезанными краями лежат одно над другим, причем одно колесо обращено выпуклой стороной вверх, а другое, смежное с ним,– вниз. Поэтому, как сказано в патенте Слонимского, «все колеса лежат в одинаковой вышине». Они свободно, не задевая друг друга, вращаются на своих осях, причем отверстия одного колеса всегда находятся между зубьями смежного.

В верхней крышке машины сделаны 4 полукруглых выреза ab, расположенных так, что в них видны отверстия в колесах. Под вырезами находится круговая шкала с цифрами от 1 до 9. Наконец круги А — D представляют собой окошки, в которых при вращении колес показываются имеющиеся на них цифры (рис. 2).

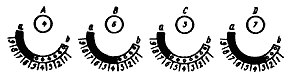
Рис. 2. Верхняя крышка машины

Число вводится в машину поразрядно. Для этого необходимо вставить штифт в отверстие, находящееся против заданной цифры на шкале под вырезом, и повернуть колесо вправо (к торцу b), если отверстие расположено на светлой части окружности, и влево (к торцу a) – если на зачерненном. Поворот осуществляется до тех пор, пока штифт не упрется в торец выреза. Если сумма складываемых цифр в любом разряде меньше 9, то штифт всегда попадает в одно из отверстий на светлой части окружности. В других случаях его надо было ставить в отверстие на черной части, и он при движении обязательно доходил до одного из зубьев колеса старшего разряда и поворачивал его на один шаг, иначе говоря, осуществлял передачу десятков.

Важно заметить, что если одно из окошек А, В, С, D, например В, содержит число 9, а мы должны повернуть к торцу a следующее колесо С, заставляя таким образом колесо В продвинуться на один зуб вперед, то в окошке В никакого числа не покажется, ибо за цифрой 9 на колесе ничего не следует. Для получения правильного результата в этом случае необходимо предварительно повернуть к торцу a колесо В, вставив штифт в отверстие, расположенное у торца b, этим действием мы прибавим 1 к числу в окошке А и заставим нуль появиться в окошке В.

Конструкция машины Слонимского допускает самопроверку правильности вычислений: всякий раз, когда одно из колес поворачивается вычислителем не так, в окошке не будет видно никакой цифры, что является индикацией ошибки.

Обратная сторона каждого колеса, а также нижняя крышка машины предназначены для выполнения операции вычитания. Здесь все знаки нанесены так же, но «с точностью до наоборот», поэтому вычитание выполняется аналогично сложению.

«Снаряд для сложения и вычитания» Слонимского – одна из наиболее простых и остроумных суммирующих машин. Она в какой-то степени перекликается с изобретением Клода Перро, но значительно проще, чем «Рабдологический абак». В последнем изобретении «узким местом» был механизм «передачи десятков», в машине же Слонимского этот узел вообще отсутствует, поскольку перенос осуществляется движением ведущего штифта.

Демидовская премия освободила Слонимского на некоторое время от забот о куске хлеба. Он переезжает в тихий польский городок Томашев, где занимается научными изысканиями. Ряд его изобретений того времени относится к самым разнообразным областям техники. Так, в 1849 году он получает патент на «усовершенствование паровой машины, при котором сила пара сообщала бы непосредственное круговращательное движение», а в 1858 году предлагает схему телеграфной связи, позволяющую одновременно вести две передачи и два приема и получившую впоследствии название «квадруплекса». Слонимский обратился в Главное управление путей сообщения за средствами для практического внедрения своей схемы, но получил отказ. А примерно через тридцать лет великий американец Томас Альва Эдисон вновь изобрел «квадруплексную связь».

В Томашеве Слонимский подготовил к изданию самую свою «рисковую» книгу «Мезиат Ганефеш Векиюма» («О бессмертии души»). Следуя своей практике обхода острых углов, он сначала в строгом соответствии с теологической ортодоксией излагает взгляды талмудистов по данному вопросу, а затем постепенно обращает внимание читателя к естественно-научному знанию, знакомя его с основами оптики, электричества, магнетизма и т. д., и, наконец, излагает (правда, в завуалированной форме) принцип единства всех сил природы. Написанная простым и ясным языком, книга пользовалась огромной популярностью у читателей самого различного образовательного уровня.

В 1858 году в связи с празднованием 90-летия Александра Гумбольта Слонимский снова едет в Берлин, где издает свою очередную книгу, посвященную биографии и научным трудам юбиляра, а также краткому изложению его «Космоса». В знак признательности Гумбольту он преподносит ему рукопись своей книги. В ответ всемирно известный ученый так пишет скромному самоучке:

«Многоуважаемый г-н Слонимский! Я очень виноват перед Вами, что так долго медлил с благодарностью... Хотя и чуждый еврейской литературе, но с ранней юности связанный с благороднейшими из ваших единоверцев, и как пламенный и постоянный поборник ваших прав, в которых вам так часто отказывают, я не могу оставаться равнодушным к той чести, которую вы мне оказали...»

В Берлине же Слонимский начинает издавать научно-популярную газету «Гацифира» («Рассвет»). Впоследствии он переносит издание газеты, которая с 1886 года стала ежедневной (!), в Варшаву и до самой своей смерти (в 1904 году) продолжает оставаться ее редактором и основным автором.

«Числительный снаряд» Слонимского не получил распространения в России потому, вероятно, что не нашлось предпринимателя, который бы взялся за его промышленное изготовление. Такая же судьба постигла и «арифметический прибор» петербургского учителя музыки Куммера (однофамильца известного математика).

Идея этого прибора заимствована изобретателем у Слонимского, однако Куммер использовал вместо зубчатых колес кремальеры (точно так же, как это сделал в свое время Клод Перро), что еще в большей степени упростило работу и конструкцию прибора.

Вряд ли изобретения Слонимского и Куммера, будь они даже «приняты к производству», выдержали бы конкуренцию с русскими счетами. Однако за границей идея Слонимского – Куммера была подхвачена многими изобретателями. Так, в 1891 году во Франции появляется «арифмограф» Тронсе, лишь несколько видоизмененный по сравнению с прибором Куммера, в следующем году – прибор Эггиса и т. д.

Интересно, что в 1949 году артель «Музремонт» в Днепропетровске выпустила счетную машину «Прогресс», которая в принципе ничем не отличалась от прибора Куммера. В отзыве авторитетной комиссии, давшей оценку машине, говорилось: «Машина может быть полезна инженерам-проектировщикам, научным работникам, студентам вузов и счетным работникам, т. к. она в очень значительной степени облегчает расчетную работу и дает в результате точное значение суммы...»

Прекрасный отзыв для изобретения столетней давности!

Примечание

1. Демидовская премия Императорской академии наук существовала с 1831 по 1865 год. Камергер П.Н. Демидов пожертвовал Академии наук 20000 рублей ассигнациями ежегодно для поощрения молодых ученых.

Из цикла статей напечатанных в журнале “Подводная лодка”, опубликованных в 1998-1999 году.
Статья опубликована в журнале “Подводная лодка” № 6, 1998 г.
Перепечатывается с разрешения автора

Статья помещена в музей 07.06.2008 года