Из истории развития аналоговых вычислительных машин в России

А.Д. Смирнов, Г.М. Петров

Принято считать, что ХХI век будет веком информатики. Информатика — это обширная область человеческой деятельности. Она состоит из трех взаимообусловленных частей: технических, программных и алгоритмических средств. Бурное развитие информатики связывают зачастую с появлением и развитием электронной техники и средств связи, объединяя их термином hardware, но без программного обеспечения — software — машины никому не нужны. О третьей составляющей — алгоритмическом обеспечении нередко забывают. Эта часть была уже ранее разработана для численного решения многих задач. И программы для ЭВМ составляются в основном для уже имеющихся алгоритмов. Действительно, при наличии алгоритма составление для него программы это, как правило, вопрос времени, а разработка самого алгоритма — более трудный и творческий процесс.

Академик А. А. Дородницын неоднократно предлагал ввести термин brainware для третьей — алгоритмической части информатики, чтобы о ней не забывали. Создания алгоритмов бурно шло еще со времен Ньютона. Особенно нуждались в точных расчетах в XVIII в. так называемые корабельные науки, требующие расчета устойчивости и усилий, возникающих в конструкции корабля при качке, определения «ходкости» и устойчивости корабля под парусами, расчета нагрузок на конструкции корабля от отдачи орудий и т. д.

Обращаясь к истории, следует признать: еще великий Эйлер, академик Российской АН, считал математику единой. В ней он видел как цель исследований, так и могучий метод решения конкретных задач, который, по существу, для многих ранее нерешенных задач на базе дифференциального и интеграг.ного исчисления давал алгоритмы их решения.

Огромное признание во всем мире получили книги Эйлера «Scientia Navalis» («Корабельная наука», 1743 г.) и «Examen des eflar que tauttes les pieses du navire ont a sapported pendant le raulis et le tangage» (1770 г.) — более полное и глубокое руководство по проектированию и расчету корабля, удостоенное премии Парижской академии наук. Это руководство послужило основой для работы Рида «Рациональное построение железных судов».

К сожалению, в ХIХ-ХХ вв. в связи с дальнейшим развитием теоретических исследований по различным разделам математики стали отделять прикладные вопросы математики от чисто абстрактных, «высоконаучных».

Известный алгебраист Д. Буль с гордостью говорил, что он изобрел такую абстрактную и изящную алгебру, которая никогда не будет востребована для практических задач (к счастью, он ошибся). Многие теоретики, изобретая хороший алгоритм, сами не доводили его «до числа», да и описывали часто на латыни, которой в ХIХ в. многие ученые (за исключением медиков) не владели.

Вычисления в руководствах и пособиях проводились, как правило, с 10-12 значащими числами, многие данные брались из опытов, и можно сказать, что при тогдашней точности измерительных приборов в таких данных верными были от силы 4-5 значащих цифр.

Несмотря на то что в конце XVIII в. было создано много алгоритмов для решения практических задач, вычисления по этим алгоритмам были чрезвычайно трудоемки. Наибольшие объемы работ возникали в астрономии, баллистике, навигации. О необходимости машинизации этих работ Г. В. Лейбниц писал еще в начале XVIII в.: «Недостойно одаренному человеку тратить, подобно рабу, часы на вычисления, которые, безусловно, можно было бы доверить любому лицу, если бы при этом применить машину».

Началось создание цифровых механических машин для выполнения арифметических операций, так называемых арифмометров. В разработку конструкции арифмометров внесли значительную лепту русские ученые и инженеры. Академик П. Л. Чебышев неоднократно обращался к исследованию механизмов. Именно точная, строгая постановка задачи в теории механизмов и исследование ее решения привели его к блестящим математическим открытиям.

П. Л. Чебышевым были исследованы механизмы счетных машин. Он решил, что наиболее сложные и ненадежные решения возникают при дискретном переносе между разрядами и предложил эпициклический механизм с плавным переносом, который впоследствии был использован американской фирмой «Мерчент» в серийных вычислительных машинах, выпускавшихся до 50-х годов XX столетия.

Попытка применить в счетных машинах колеса с переменным числом зубцов была впервые предпринята еще итальянцем Джованни Пеленом в 1709 г. Однако создать на этой базе надежную простую конструкцию никому в течение 150 лет не удавалось. Только в 1874 г. инженер Экспедиции заготовления государственных бумаг в Петербурге В. Т. Однер предложил надежную и простую конструкцию такого колеса — знаменитое «колесо Однера». Это колесо стало основным узлом многих арифмометров. В нашей стране арифмометры Однера выпускались вплоть до 60-х годов XX в.

Так развивалась линия арифмометров, перешедшая затем в линию клавишных вычислительных машин. С заменой механических счетных устройств электронными она перешла в линию электронных калькуляторов, которая в наше время для старших моделей слилась с линией персональных ЭВМ.

В начале XX в. (в 1906 г.), выдающийся русский математик, механик и инженер-кораблестроитель академик А. Н. Крылов, озабоченный тем, что в современных курсах математического анализа доказывается существование решения какой-либо проблемы и теоретическая возможность получения его с любой степенью точности, но при этом не уделяется внимания получению такого решения с точностью, необходимой для практических целей, решил исправить это положение.

Им был составлен курс о приближенных вычислениях, приемах и способах: вычисление корней численных уравнений, и определенных интегралов, пользование тригонометрическими рядами и приближенное решение дифференциальных уравнений.

Книга «Лекции о приближенных вычислениях» была первым в мировой литературе курсом такого направления и послужила образцом для последующих, вышедших после нее курсов других авторов. Этот классический курс выдержал пять изданий (три из них при жизни автора). В главе IV описывается также общая теория и конструкция механических приборов для вычисления определенных интегралов. Это механические приборы, в которых исходные данные и результаты представляются не в цифровой форме, а в виде линейных или угловых перемещений частей этих приборов.

А. Н. Крылов изобрел прибор для фотозаписи качки корабля (1913 г.), планометр-топорик (1908 г.), создал полную теорию разработки и оценки точности планиметров. Он построил прибор для решения обыкновенных дифференциальных уравнений (1911 г.). А. Н. Крылов, по скромности, не уточнял, какие алгоритмы численного решения или какие части счетно-решающего аналогового устройства разработаны лично им, но очень скрупулезно отмечал источники, послужившие прототипом для них или натолкнувшие его на те или иные выводы. Так, современники указывают, что на базе морского компаса, хронометра и лага (прибора для измерения скорости корабля) Крылов создал прибор, автоматически вычерчивающий на карте путь, проходимый кораблем, гироскопический успокоитель качки (раньше Сперри), полную теорию гироскопа.

Им были разработаны или улучшены многие алгоритмы вычислений в области корабельных наук и баллистики, в 1896 г. он представил полную теорию качки корабля (3-мерный случай).

Свободно владея несколькими языками, он полностью перевел с латыни «Математические начала натуральной философии» И. Ньютона (в 1915-1916 гг.), сделав при этом 207 примечаний.

Из переписки Наполеона он выбрал и перевел места, относящиеся к науке. Не мешало бы их издать отдельной брошюрой для наших правителей и законодателей.

Ссылаясь на Фурье и Больцмана, А. Н. Крылов напомнил, что единство законов природы выражается в том, что разные явления описываются одними и теми же дифференциальными уравнениями, и, найдя решения уравнений, мы сразу решаем задачи для целого ряда наук.

Тот факт, что различные физические явления описываются одинаковыми математическими уравнениями, отмечался многими учеными: Больцманом, Гексли и др. А. Н. Крылов сформулировал это явление достаточно точно, но не дал заключения о возможности создания на его основе вычислительной машины. Такой вывод сделал другой русский академик Н. Н. Павловский в 1918 г.

Для приближенного решения уравнения Лапласа, которым описываются фильтрация подземных вод, потенциальное обтекание тел потоком несжимаемой жидкости, стационарный поток тепла в нагреваемой металлической пластинке, установившийся электрический поток в электролитической ванне и т. д., можно создать электрическую модель с электролитической ванной. И если область решения и граничные условия будут такими же, как для плоской задачи фильтрации воды под плотиной, то можно установить соответствие переменных величин в гидравлической задаче их аналогам в электрической и получить решение, измеряя электрическую величину (напряжение), которая является аналогом давления воды в гидравлической задаче.

Павловский назвал этот метод аналогового моделирования ЭГДА (электро-гидродинамический аналог). За вычислительными системами, использующими этот метод, закрепилось наименование аналоговых (АВМ), в отличие от цифровых (ЦВМ),

Приборы ЭГДА получили широкое применение как у нас в стране, так и за рубежом при расчете гидросооружений, решении задач фильтрации нефти, в гидродинамике.

Если коэффициент фильтрации грунта в исследуемой области неравномерный, то дно электролитической ванны делалось из парафиновой пластинки переменной толщины для отслеживания коэффициента фильтрации грунта. Точность модели ЭГДА определялась точностью электроизмерений и точностью изготовления ванны.

В развитии метода ЭГДА большую роль сыграла работа ленинградского математика С. А. Гершгорина, который предложил заменить электролитический (токопроводящий) слой раствора в ванне сеткой из сопротивлений.

Это было аналоговой моделью замены дифференциального уравнения Лапласа конечноразностной схемой. Точность такой модели теперь зависела и от шага сетки. Точность можно было увеличить, сгущая сетку в местах больших градиентов искомой функции (вводя как бы «электрическую лупу»).

Делая сопротивление сетки переменным, можно было решать более сложное уравнение с переменными коэффициентами, а подключая к узлам сетки емкости (конденсаторы), — моделировать уравнение Фурье (теплопроводности), т. е. уравнение параболического типа.

Дальнейшее развитие электроинтеграторов сеточного типа осуществлялось коллективом под руководством проф., д.т.н. Л. И. Гутенмахера.

В серии были выпущены электроинтеграторы ЭИ-12 для решения уравнений эллиптического типа с переменными коэффициентами и ЭИ-22 с конденсаторами в узлах сетки для решения параболических задач.

Помимо развития электроинтеграторов сеточного типа в Институте железнодорожного транспорта д.т.н., проф. В. С. Лукьянов в качестве аналоговой применил сетку из переменных гидравлических сопротивлений. Каждое сопротивление представляло собой трубочку с коаксиально входящим в нее стержнем. Вода протекала по цилиндрическому пространству между трубочкой и стержнем. Чем глубже вставлен стержень в трубочку, тем больше сопротивление. В узлах сетки подсоединяются емкости, причем они могут быть переменного сечения, т. е. решаются уравнения параболического типа с нелинейностями.

Коэффициент 1/RC в уравнении Фурье моделирует масштаб времени. Можно решать задачу в натуральном масштабе времени, в замедленном (например, моделировать сварку или взрыв, занимающие 1 с, в течение 100 с), разбираясь во всех тонкостях процесса, или в ускоренном (например, за 10 мин проследить осадку грунта в плотине или таяние ледника, проходящие в естественных условиях в течение 10 лет).

В. С. Лукьянов, будучи инженером путейцем, ставил сам и совместно с акад. Патоном задачи сварки железнодорожных мостов, строительства в условиях вечной мерзлоты.

В узлы сетки могут подключаться плавающие сосуды, заполняющиеся или сливающие в сеть воду при моделировании t=0°С, замерзания воды или оттаивания.

Была решена классическая и очень важная задача для нашего Севера — определение оптимальной изоляции и глубины заложения магистральных теплотрасс в условиях вечной мерзлоты. При этом и потери тепла минимизировались, и разрушение вечной мерзлоты не допускалось. Задача была нестационарной, т. е. параболического типа и существенно нелинейной.

Конструкция, надежность и легкость эксплуатации гидроинтегратора была такова, что он выпускался в трех вариантах до конца 80-х годов (образцы гидроинтегратора и сеточные электроинтеграторы представлены в коллекции московского Политехнического музея). На них были решены многие двумерные и даже трехмерные задачи нестационарной фильтрации, задачи теплопередачи в зданиях, инженерных сооружениях (например, в теле плотины), исследованы температурные поля (а через них и напряжения температурной деформации) при сварке металлов, решена большая серия задач по теплопередаче в мерзлом и талом грунтах с учетом поглощения или выделения тепла при оттаивании и замерзании грунта, что имело важнейшее значение при освоении районов Дальнего Севера.

Интеграторы на электрических сеточных моделях ЭИ-12 для решения уравнений эллиптического типа и ЭИ-22 для решения уравнений параболического типа были разработаны под руководством профессора Л. И. Гутенмахера. На сеточных моделях моделировались нефтяные месторождения. Первоначально созданная модель уточнялась по натурным измерениям дебита скважин, неизвестные параметры грунта подбирались таким образом, чтобы добиться соответствия ретроспективного процесса на модели и в натуре, это являлось залогом достаточно близкого соответствия модели натуре. После этого на модели в ускоренном масштабе времени отрабатывался перспективный план оптимальной эксплуатации месторождения и затем переносился на натуру.

В конце 40-х — начале 50-х годов Л. И. Гутенмахером, Н. С. Николаевым, Н. В. Корольковым, В. Б. Ушаковым и Г. М. Петровым создаются электроинтеграторы на активных четырехполюсниках (см. рис. 1, 2) для моделирования обыкновенных линейных и нелинейных уравнений. Появление этих интеграторов позволило исследовать методом математического и полунатурного (с включением в контур моделирования реальных приборов автоматического управления, например автопилотов) моделирования сложные динамические системы. В частности, стала возможной замена некоторых летных исследований наиболее опасных режимов полета новых самолетов их полунатурным моделированием.

Таким образом, в период с 20-х до 50-х годов советская научная школа вышла на передовые позиции в решении задач методом моделирования, заложив принципиальные основы кибернетики.

В 1948 г. в СССР были созданы первые электронные аналоговые вычислительные машины (АВМ), построенные на операционных усилителях постоянного тока. Именно операционные усилители, работающие по принципу систем автоматического регулирования с глубокой отрицательной обратной связью, позволили осуществить точное моделирование математических операторов (в том числе главного — интегрирование переменных) и параллельную обработку информации в реальном времени при решении систем дифференциальных уравнений.

Благодаря этому АВМ обеспечили решение важнейших задач в целом ряде направлений науки и техники (авиации, ракетостроении, космических исследованиях, оборонной промышленности и др.). В этот период ЦВМ еще не имели необходимого быстродействия для решения подобных задач.

Первые АВМ на электронных лампах были созданы объединенными усилиями двух коллективов: НИИ-855 МРП СССР и ИАТ АН СССР. В дальнейшем этим занимались в СКБ-245, НИИСчетмаше, ИПУ АН СССР, КБ-1. Серийный выпуск АВМ был организован на Московском, Пензенском и Кишиневском заводах счетно-аналитических машин и ряде других заводов радиопромышленности. За первые 20 лет было изготовлено более 100 тыс. АВМ различной мощности — от простых АВМ типа МН-7 (общий выпуск которых превысил 25 тыс.) до самых мощных типа МН-8, АВК-2. На первом этапе (50-е годы) АВМ использовались в основном в виде самостоятельных средств математического моделирования динамических объектов в реальном времени. Часто они входили в состав тренажеров (авиационных, космических, атомных установок, транспортных средств и т. п.). Со временем (60-70-е годы) в связи с прогрессом в области цифровой электроники АВМ все чаще стали подключаться к ЦВМ для совместной обработки информации. Появился новый вид вычислительной техники — аналого-цифровые вычислительные комплексы (АЦВК). Функции АВМ и ЦВМ в этом случае существенно различались.

На рисунке представлено «дерево» развития средств АВТ и АЦВТ в СССР в период 1948-1970 гг. В их создании активное творческое участие принимали выдающиеся ученые и специалисты: Витенберг И. М., Беляков В. Г., Копай-Гора В. Н., Басов Е. П., Коган Б. Я., Москаленко Г. В., Птаховский И. Г., Шубин Ю. А., Сабаев Г. Н., Райков Л. Д., Ефремова Е. А., Голован В. А. и многие другие.

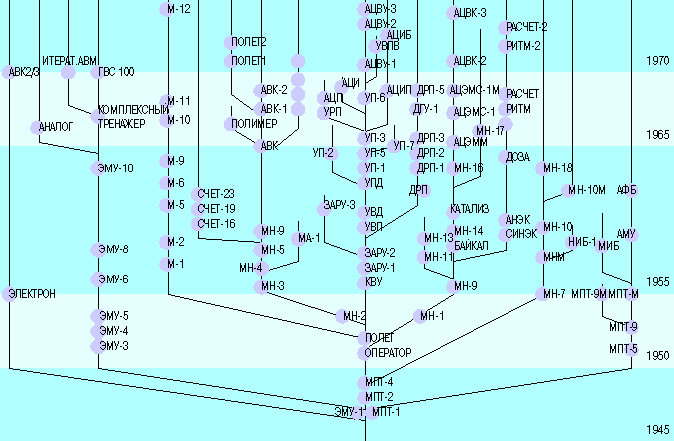
«Дерево» развития средств АВТ и АЦВТ в СССР в 1948-1970 гг.

В 1958 г. в СССР была создана первая в мире полупроводниковая АВМ МН-10. Эта машина с большим успехом демонстрировалась на выставке в Нью-Йорке в июне 1959 г.

В 60-70-х годах специалистами НИИСчетмаша, ИПУ АН СССР создана серия аналоговых и аналого-цифровых комплексов с использованием микроэлектронной элементной базы, внедренных в серийное производство на отечественных заводах радиопромышленности. Коллективу разработчиков комплексов АВК-1 и АВК-2 (главный конструктор Беляков В. Г.) в 1980 г. была присуждена Государственная премия.

В 80-х и начале 90-х гг. в НИИСчетмаше были созданы эффективные современные периферийные устройства для ввода-вывода в ЭВМ аналоговой информации в реальном времени, в их числе: двухкоординатные графопостроители, устройства автоматического распознавания графических изображений, векторные и растровые графические дисплеи, струйные и лазерные печатающие устройства, устройства автоматического распознавания речи и др.

В этом году коллектив НИИСчетмаша отмечает свой 50-летний юбилей. К сожалению, праздник омрачен тяжелым материальным положением института. За годы реформ (с 1991 г. до настоящего времени) от более чем двухтысячного коллектива осталось 30 человек. Основные производственные площади института по вине нерадивых руководителей оказались в руках Инкомбанка. Несмотря на это, НИИСчетмаш продолжает работать, надеясь на лучшее будущее.