Блуждание в трех соснах

(Приключения диалектики в информатике)

Брусенцов Н. П.

Цель памфлета — обратить внимание на недиалектичность и несподручность здравому рассуждению преобладающей в современной информатике формальной логики, унаследованные ею будто бы от Аристотеля. Указана возможность и актуальная необходимость воссоздать в информатике подлинный дух аристотелева Органона.

Философы все еще не могут договориться о том, что же значит слово информация, но практикам исчерпывающая ясность, похоже, и не нужна: неопределенность ведь в каком-то смысле свобода . Бог с ней, с информацией, практики создают информационные системы, информационные технологии (также толком не определив, что это такое), и все мы уже знаем, что очередным этапом человеческой цивилизации будет информационное общество. Впрочем, непонятно, почему бы не  виртуальное. Недоумения не будет, если в приведенных словосочетаниях вместо информационные говорить компьютерные. Конечно, не все информационное должно быть компьютерным, но в современном понимании информатизация — это не более чем компьютеризация, и слово информатика в новом смысле употребляется как синоним англоязычного computer science .

Однако по справедливости, информатика должна быть наукой об информации, т.е. об отображениях бытия не только компьютерных, но всевозможных — мысленных, письменных и устных, алгебраических, графических, изображающих, выражающих, подражающих, карикатурных и т.п. Аристотель называл эту науку первой философией, понимая ее как способ (Органон) исследования, прокладывающий “путь к началам всех учений”.

Сущность этого способа в том, что, исходя из правдоподобного отображения реальной ситуации, применением его доказательно выявляются оправдывающиеся на практике заключения об этой ситуации. Слова, которыми в нашем языке отображены объекты реальности, Аристотель уподоблял счетным камешкам в том смысле, что при помощи слов можно моделировать всевозможные взаимосвязи, подобно тому как посредством камешков моделируются взаимосвязи количественные:

“... так как нельзя при рассуждениях приносить самые вещи, а вместо вещей мы пользуемся как их знаками именами, то мы полагаем, что то, что происходит с именами, происходит и с вещами, как это происходит со счетными камешками для тех, кто ведет счет.”

Другими словами, у традиционного анализа реальных ситуаций методом проб и ошибок имеется “информационная альтернатива” - отобразить рассматриваемую ситуацию посредством слов и производить необходимые исследования полученного отображения методами аристотелева Органона, т.е. подменить физическое моделирование информационным. Разумеется, методы Органона должны гарантировать практическую подтверждаемость получаемых результатов в учтенных отображением условиях конкретной ситуации.

В Органоне функции счетных камешков выполняют термины - слова либо буквы, обозначающие критерии , по отношению к которым характеризуются рассматриваемые вещи. Сущности вещей (не только отдельных материальных предметов, но и всевозможных взаимосвязей, ситуаций, процессов, как реальных, так и мыслимых) отображаются совокупностями определенностей их в отношении принятых критериев. Например, погоду можно охарактеризовать в таких терминах, как “ветренная”, “дождливая”, “холодная”, “пасмурная”, “промозглая” и т.п. Если характеризуемая вещь удовлетворяет данному критерию, соответствующий термин входит в ее определение непосредственно, в утвердительной форме, а если не удовлетворяет, то в отрицательной - под знаком отрицания . В русском языке таким знаком служит, как правило, частица не (“не-ветренная”, “не-холодная”), а друг с другом термины, и утверждаемые, и отрицаемые, связываются выражающим совместность соответствующих определенностей союзом и , который в многочленных определениях обычно опускают. Вместо “ветренная, и дождливая, и холодная" говорят “ветренная, дождливая и холодная" или “ветренная, дождливая, холодная”.

Подобная форма определения сущности вещи в булевой алгебре называется элементарной конъюнкцией. Терминами в алгебре, как и в Органоне, служат буквы, поскольку исследуются не конкретные критерии и определенности, а виды взаимосвязей, применяемых к определенностям любой природы. В роли связки и употребляется знак конъюнкции (совместности) Λ , который, подобно знаку умножения в числовой алгебре, обычно умалчивают (опускают) - вместо xΛy пишут xy . Нередко конъюнкцию называют логическим умножением, хотя как раз умножения в ней нет - в отличие от умножения x•x=x² она идемпотентна: xΛx=x . Впрочем, следуя Булю, можно рассматривать ее как умножение чисел, допускающих только два значения: 1 - “дано”, 0 - “исключено”.

В булевой алгебре вместо не - x пишут ¬x, либо надчеркнутое x , либо x'. Применительно к несоставному, не детализируемому в рамках проводимого рассмотрения, термину эти символы тождественны друг другу, синонимы. Однако в общем случае, когда буква обозначает произвольное булево выражение, их следует различать либо вводить какие-то иные знаки для представления возникающего многообразия взаимосвязей. Условимся, что постфикс ' обозначает инверсию выражения, префикс ¬ - дополнение в универсуме терминов-критериев, а надчеркивание употреблять не будем.

Применительно к двучленной конъюнкции xy это значит :

(xy)'=x'y'

¬(xy)'=x'νy'

Знак ν символизирует дизъюнкцию - взаимосвязь, двойственную конъюнкции, в русском языке представленную союзом или . Двойственность понимается в том смысле, что произвольное выражение булевой алгебры, если в нем заменить конъюнкции дизъюнкциями, а дизъюнкции конъюнкциями, будет представлять ту же взаимосвязь при условии, что значение 1 истолковывается как 0, а значение 0 - как 1. Так, xy = 1 означает совмещение двух: x = 1 и y = 1, а xνy = 0 соответственно x = 0 и y = 0, т.е . конъюнкция отображает совместность единиц, а дизъюнкция - совместность нулей. С другой стороны, при xνy =1 термины x , y несоисключимы, не могут вместе принять значение 0, а при xy = 0 они несовместимы , исключена совместность 1.

Заметим, что дополнение булева выражения двойственно его инверсии: в приведенном примере дополнительное выражение x' ν y' отличается от инверсного x' Λ y' тем, что в нем заменен двойственным (перевернут, “инвертирован”) знак Λ . Взаимосвязь операций инверсии, дополнения и получения двойственного (“дуалирования”) δ ( διπλοη - двойственное) булева выражения e представима тождествами:

e'δ(¬e) ¬(δe),     ¬e (δe')(δe)',     δe¬(e')(¬e)'

Странно, что это фундаментальное соотношение выявлено не логиками и не математиками, а психологом Жаном Пиаже. Впрочем, не странно, ибо логики и математики приучены к булевой алгебре с единственной одноместной операцией отрицания-дополнения, которую иногда называют также инверсией, либо полагают, что инверсия - операция не булева, а теоретико-множественная, множественное дополнение.

Джордж Буль изобрел “математику мысли”, устранив из числовой математики все значения, кроме 0 и 1, интерпретируемых как “нет" и “есть”, либо “исключено” и “дано”, либо “ложь” и “истина”. Такую систему называют двузначной , что не представляется верным, ибо двузначность - синоним двусмысленности. Корректней назвать ее двухзначной системой, двухзначной логикой. Но это только поверхностное, “косметическое" уточнение, а по существу проблема двухзначности несравненно глубже, фундаментальней. Противопоставленный стоиками аристотелеву Органону хрисиппов принцип двухзначности в его “классической" трактовке (либо истина, либо ложь и ничего третьего) радикально отделил формальную логику, и традиционную, и математическую, от диалектики.

Впрочем, основоположник математической логики Буль, не в пример современным представителям этой науки, сосредоточившим все внимание на проблеме двухзначного (дихотомического) вывода, считал важнейшей ее задачей решение логических уравнений, чем и оправдывалось название “математическая”. Решение этой обратной задачи, предпринятое самим Булем, показало, что удовлетворяющим логическому уравнению значением термина может быть не только 1 либо 0, но и нечто третье - “неопределенность”, которую Буль обозначал буквой u ( u0/0). В дальнейшем выяснилось, что в зависимости от условий, определяемых значениями прочих входящих в уравнение терминов, для искомого термина x имеется четыре альтернативы:

1. x = 0,
2. x = 1,
3. x свободно, не фиксировано (у Аристотеля - “привходяще”),
4. решение не существует.

Например, решение относительно термина y уравнения xy = 0, как нетрудно проверить, таково: при x = 0 значение y привходяще, при x = 1 y = 0. Решение уравнения x ν y = 0, т.е . x'y' = 1, при x = 1 не существует, при x = 0 y = 0.

Как члены элементарной конъюнкции, которой охарактеризована рассматриваемая вещь, скажем, xy', термин x утверждается, а термин y , входящий в конъюнкцию под знаком отрицания, отрицается относительно этой вещи. В духе Аристотеля можно сказать, что определенность x необходимо присуща данной вещи, а присущность ей определенности y исключена, она антиприсуща. Но по Аристотелю определенность может быть, кроме того, привходящей , т.е. не присущей и не антиприсущей с необходимостью, а - то быть, то не быть, как попало. Представляющий такую определенность термин, скажем, z , рассматриваемая конъюнкция не содержит ни в утвердительной, ни в отрицательной форме, он не утверждается и не отрицается. Строго говоря, определенность z в этом случае будет потенциально привходящей - возможно присущей, возможно антиприсущей, возможно привходящей. Актуально привходящее, исключающее возможность присущности и возможность антиприсущности, в “классической" двухзначной системе невыразимо.

Буль наряду с операцией отрицания применял операцию элиминации (устранения) термина, которая была затем усовершенствована П.С. Порецким. Выходит, что и в двухзначной булевой алгебре термин можно либо утверждать, либо отрицать в смысле антиутверждать, либо не утверждать и не отрицать, а “элиминировать”, устранить из выражения, “опустить”.

Обращаясь к древним грекам, нетрудно убедиться, что в логике их языка хрисиппова двухзначность не доминировала, но впоследствии привела к такому искажению смысла слов, обозначающих базисные взаимосвязи, что написанное Аристотелем стало непостижимым. Слова: καταφασις - утверждение, αποφασις - не-утверждение, αντιφασις - анти-утверждение, составляющие основу аристотелева соотнесения объектов (“быть благом”, “не быть благом”, “быть не благом”; “Всякое А есть Б”, “Некоторое А не есть Б”, “Всякое А есть не Б”), стали понимать иначе, будто αποφασις - “отрицание”, αντιφασις - “противоречие”. Но ведь и απο - и αντι - означают отрицание и оба порождают выражения, противоречащие утверждению. В чем же логика?

По Аристотелю конъюнкция не-утверждения и не-антиутверждения (“не быть благом и не быть не благом”) составляет третье , среднее, промежуточное между утверждением и антиутверждением - συμβεβηκος (привходящее). Хрисипп же “упростил" логику, изъяв это третье, а вместе с ним адекватность реальности и здравому смыслу. У него дискретная дихотомия - “да”/“нет”, поэтому αποφασις αντιφασις , “не быть благом” “быть не благом”. Это мир “рыцарей” и “лжецов” из “занимательной логики”: “рыцарь” никогда не лжет, “лжец” лжет всегда; если некто не “рыцарь”, то он “лжец”, а если не “лжец”, то “рыцарь”. Все четко и просто, но не так, как в действительности.

Поразительна живучесть хрисипповой “простоты”. На протяжении двух с лишним тысячелетий имели место лишь единичные попытки преодолеть роковую ограниченность (Раймонд Лулий, Уильям Оккам, Ян Коменский, Лейбниц, Гегель, Льюис Кэррол).

Двадцатый век ознаменован прогрессирующим нарастанием протеста против двухзначности: отвержение интуиционистской математикой закона исключенного третьего, попытки Льюиса, а затем Аккермана преодолеть “парадоксы" материальной импликации, изобретение Лукасевичем трехзначной логики, предположение Рейхенбаха о трехзначности логики микромира (квантовой механики), общее усиление активности в области многозначных логик, наконец, нечеткие множества Заде, справедливо квалифицируемые “как вызов, брошенный европейской культуре с ее дихотомическим видением мира в жестко разграничиваемой системе понятий”. Однако все это пока как бы некий “модерн”, не достигающий преследуемых целей, да и сами цели еще далеко не осознаны. Хрисиппова же “классика” обрела второе дыхание в исчислениях математической логики, в двоичной цифровой технике, и с позиций ее столь же непросто постичь недвухзначное, как, скажем, обитателям двухмерного мира представить себе мир трехмерный.

Показателен пример Яна Лукасевича, который, связывая создание им трехзначной логики “с борьбой за освобождение человеческого духа”, затем (надо полагать, в продолжение этой борьбы) в своей неординарной книге “Аристотелева силлогистика с точки зрения современной формальной логики" устанавливает “ошибочность” положений трехзначной логики Аристотеля, формально “верифицируя” их в двухзначном исчислении высказываний. Впрочем, его попытки формализации модальностей средствами трех- и четырехзначного исчислений также не достигли цели. Он обратился к многозначности, осознав, что “модальная логика не может быть двухзначной”, однако не сумел преодолеть традиции и выявить трехзначность аристотелевой силлогистики, чего ранее уже достиг поборник “эмансипации логики от влияния Аристотеля” Н.А.Васильев, в 1911 году преобразовавший логический квадрат A - I - O - E в треугольник противоположностей A - I O - E .

Этот треугольник и есть “три сосны”, в которых заблудились логики 20-го века в попытках изобрести то, что в древности естественно и неопровержимо установил Аристотель. Изобретать вынуждала неадекватность двухзначной логики, в частности, невыразимость в ней сущности естественноязыкового (содержательного) следования. Первой, получившей значительный и все еще не угасший резонанс, была попытка Льюиса (1918 г.) устранить “парадоксы” материальной импликации, модифицировав аксиоматику классического исчисления высказываний. Но “строгая импликация” Льюиса оказалась тоже парадоксальной, да и неясно, что она такое, поскольку при помощи связок двухзначного исчисления определить конструктивно ее нельзя, а введенная в него “модальная функция самосовместимости-возможности” в свою очередь лишена определения.

Импликация Лукасевича (1920 г.) определена трехзначной таблицей истинности, но как заметил полвека спустя Слупецкий, смысл ее “довольно-таки неуловим”. Сам Лукасевич впоследствии, признав трехзначное исчисление недостаточным, разработал четырехзначную модальную логику, однако именно его трехзначная импликация инициировала необыкновенную активность в области трехзначных логик и алгебр, в результате которой теперь имеется множество импликаций (интуиционистская Гейтинга, сильная и слабая Клини, внешняя и внутренняя Бочвара, Геделя, Собочинского...), смысл которых столь же неуловим и, увы, не тождествен содержательному следованию. Это удивительное блуждание в трех соснах обусловлено тем, что ищут, не зная что. Операции определяются не путем воплощения подразумеваемого смысла, а либо формальным обобщением соответствующих двухзначных таблиц истинности, в частности, таблицы материальной импликации, истолкование которой в свою очередь проблематично, либо модификацией системы аксиом, например, изъятием закона исключенного третьего.

Таблицы истиности

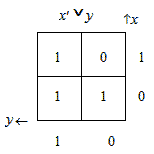
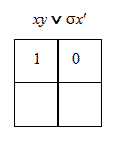
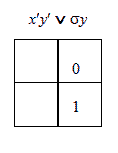
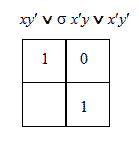
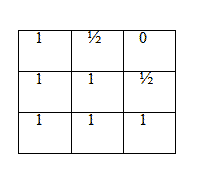
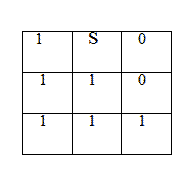
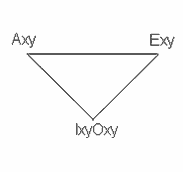
        Импликация Лукасевича           Импликация Гейтинга           Треугольник Н.Васильева

Разобраться в силлогистике удается не путем формального построения трехзначных и многозначных логик, а осмысленным последовательным развитием двухзначной логики, находящейся в ее основании. В качестве необходимых начал доказательного рассуждения (“без которых невозможно рассуждать”) Аристотель принял в сущности принцип двухзначности: “... что относительно чего бы то ни было необходимо или утверждение, или отрицание и что невозможно в одно и то же время быть и не быть”. По этому принципу, получившему наиболее совершенное воплощение в булевой алгебре, у Аристотеля посредством терминов определены сущности рассматриваемых вещей (“первые сущности”). “Камешки”-термины предполагаются четко различимыми, дискретными, подобно целым числам. Однозначная характеристика вещи представляет собой элементарную конъюнкцию всех уместных терминов, утверждаемых либо отрицаемых, а неоднозначная, нечеткая, характеристика - дизъюнкцию таких конъюнкций, в частности, попарно склеиваемых.

Другими словами, вещи охарактеризованы совокупностями терминов, четкими либо нечеткими. Это 1-я ступень силлогистики, изоморфная классической логике высказываний, булевой алгебре терминов, пополненной теоретико-множественными операциями инверсии, пересечения и объединения выражений. Она позволяет рассуждать о совокупностях терминов, характеризующих единственную и единую рассматриваемую “вещь” (в широком смысле слова), выявляя отношения, которыми термины связаны друг с другом “в мире этой вещи”. Но силлогистика исследует совокупности различных вещей, т.е. совокупности совокупностей терминов. Поэтому в Органоне необходима 2-я ступень, которую естественно и проще всего реализовать, воспользовавшись теми же булевыми связками (конъюнкцией, дизъюнкцией, отрицанием-дополнением, а также инверсией, пересечением и объединением), однако на сей раз применительно не к атрибутам вещей непосредственно, а к охарактеризованным ими вещам и к совокупностям вещей.

В отличие от представленной элементарной конъюнкцией терминов четкой совокупности 1-й ступени, означающей их совместность (единство) и присущность символизируемых ими определенностей охарактеризованной ею вещи, четкая совокупность (множество) 2-й ступени означает сосуществование в ней, или сопринадлежность ей различных вещей, сущности которых попарно несовместимы. Такая совокупность представима конъюнкцией существований, в которой существование вещи, охарактеризованной, скажем, атрибутом xy', обозначается дизъюнктом V xy' . Например, множество, которому принадлежат сущности xy' и x'y , но не принадлежат xy и x'y' , обозначаемое в математике как {xy', x'y}, выражается конъюнкцией дизъюнктов V'xyVxy'Vx'yV'x'y' .

Как видно, Vx - конструкция, аналогичная сумме Σx , однако означает не суммирование, а дизъюнкцию значений, принимаемых термином x на элементах рассматриваемого множества (данной совокупности “вещей”). Наглядной моделью совокупности является “урна Лукасевича”, в которой элементы представлены шарами, помеченными присущими им терминами. Наличие в урне хотя бы одного шара, помеченного буквой x , есть принадлежность данной совокупности элемента, которому присуще x (который удовлетворяет критерию x), а короче - принадлежность x , существование x , Vx = 1. Урна, в которой x - шаров нет, символизирует антипринадлежность x, Vx=0, V'x=1 . Наличие в урне шаров, не помеченных буквой x , есть принадлежность x', Vx'= 1 , отсутствие - антипринадлежность x', V'x'=1. Наличие x - шаров при отсутствии x' - шаров представляет собой совокупность VxV'x', которой x необходимо присуще в целом. Урна же, в которой нет ни x -, ни x' - шаров, символизирует пустую совокупность V'xV'x' .

Принадлежность вещей, охарактеризованных по нескольким критериям, представляется дизъюнктами с соответствующими элементарными конъюнкциями, например: Vxyz, Vxyz' , Vxy'z и т.д.

В самом простом случае различения по единственному критерию x имеется два вида вещей: x, x' и четыре качественно различных четких совокупности (множества):

VxVx' - полная совокупность, ей принадлежат (сопринадлежат) оба вида;
VxV'x' - одноэлементная совокупность, принадлежность только вида x, присущность x всем членам совокопности;
V'xVx' - принадлежность только вида x';
V'xV'x' - пустая совокупность.

Дизъюнкцией этих четырех конъюнкций (они несоисключимы и попарно несовместимы) исчерпывается характеристика произвольной однокритериальной совокупности вещей, однокритериального общего универсума (УО):

VxVx' ν VxV'x' ν V'xVx' ν V'xV'x'1

Это СДНФ-выражение 2-й ступени можно минимизировать, получив ослабленную версию законов исключенного третьего и противоречия:
Vx ν V'x1,   VxV'x 0.

Исключение из УО тех или иных его частей порождает специальные универсумы, в частности, представляющие особый интерес для упорядочения логики :

непустой (интуиционистский) универсум (УИ) -
VxVx' ν VxV'x' ν V'xVx'Vx ν Vx'1, V'xV'x' 0 ;

трехзначный дискретный универсум Поста (УП) -
Vx V'x' ν V'x Vx' ν V'x V'x'V'x ν V'x'1, Vx Vx'0 ;

двухзначный универсум Хрисиппа-Буля (УБ) -
Vx V'x' ν V'x Vx'1, Vx Vx' ν V'x V'x'0 ;

универсум Аристотеля (УА) -
Vx Vx'1, V'x ν V'x'0 ;

пустой универсум -
V'x V'x'1, Vx ν Vx'0 .

В приведенном фрагменте иерархии универсумов наглядно отображена иерархия важнейших логик:

в УО имеет место четырехзначная логика, в которой термин x можно охарактеризовать как необходимо присущий - Vx V'x' , необходимо антиприсущий - V'x Vx' , привходящий - Vx Vx' , ничего не представляющий, немыслимый - V'x V'x' ;
в УИ устранено пустое - предметная область непуста, логика трехзначна: присуще / привходяще / антиприсуще;
в УП исключено привходящее, осталось три четко различимых состояния - дискретная трехзначная логика;
в УБ исключены пустое и привходящее, осталось два четко различимых состояния - дискретная двухзначная логика;
в УА исключены дискретные состояния, термин определен сосуществованием противоположностей Vx Vx' , т.е. так как оно и есть в реальности.

С пониманием того, как устроена иерархия логик, открывается возможность конструктивно определить модальные функции и отношения, не изобретая их “по интуиции”. Очевидно, что базисной модальной функцией должна быть простейшая и инвариантная по всем универсумам - актуальная возможность , или существование , т.е. дизюнкт Vx , сущность которого охарактеризована выше. У Льюиса это ◊x - самосовместимость, и вместе с тем 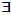x - существование , у Лукасевича: M x - “ простая ” возможность и 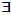x - существование . Ни Льюис, ни Лукасевич не обнаружили, что их модальные функторы ◊, M означают то же, что и кванторы по терминам-предикатам 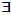, Σ, т.е. что
◊x Σx M x Σx Vx

Этой же функцией является замыкание Cx в алгебрах с замыканиями. Для нее выполняются тождества:
¬M x M'x,   Mx ν ¬M xMx ν M'x1

Посредством нее определимы другие модальные функции и соответствующие кванторы.

Аристотелева актуальная необходимость L x определяется в виде:
L x VxV'x'MxM'x'

В УИ это определение упрощается в LxV'x'M'x' , однако в УО выражение M'x' означает лишь потенциальную необходимость , которой соответствует квантор общности 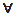по предикатам в его “математическом”, не в естественноязыковом, смысле:

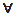x Λx V'x'M ' x'

Модальная функция QxMxMx' - случайность, акцидентальность, выявляет аристотелево привходящее Vx Vx' : термин x обладает значением σ (συμβεβηκος), если Q x 1. Символ σ обозначает промежуток между утверждением и антиутверждением: 0 < σ< 1. В теории вероятностей 0 - невозможность, 1 - достоверность, а все прочие значения в совокупности составляют логическое σ . У Буля и у Порецкого имеется процедура пробабилизации - перевода булевых выражений по существу на язык нечетких множеств Заде.

В УБ с устранением привходящего, а вместе с ним и Q x , функции M x и L x вырождаются, отождествляясь с их аргументом - двухзначным термином:
MxVxVxV'x'x , LxVxV'x'x

В УА, наоборот, все термины необходимо привходящи, и именно поэтому “строгая импликация” Льюиса ~ ◊(x ~ y), т.е. V'xy', оказывается здесь полноценным содержательным следованием, в точности соответствующим аристотелеву определению [“Первая аналитика”, 57b1], в котором Лукасевич усмотрел “ошибочное” с точки зрения современной формальной логики положение. В алгебре совокупностей 2-й ступени это определение представлено выражением VxV'xy'Vy' , означающим нечеткое множество, которому необходимо принадлежат x -элементы и y' - элементы, и антипринадлежат xy' - элементы, так что всякий его x - элемент непременно есть y - элемент, всякому x присуще y .

Замечательным графическим аналогом алгебры дизъюнктов является диаграмма Льюиса Кэррола, наглядно отображающая совокупности 2-й ступени с не более чем тремя терминами в формате “таблицы истинности”, интерпретируемой как разбиение универсума на классы по принятым терминам-критериям.

Диаграммы Льюса Кэррола

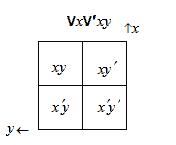
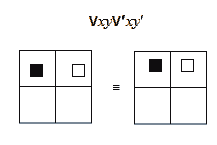
Классы xy -универсума       “Всякое x есть y” (буквально)

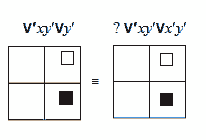
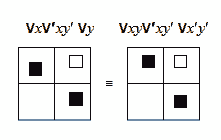
      “Всякое y' есть x' ” (буквально)     “Всякое x есть y ” (следование y из x )

Следует заметить, что выражение VxV'xy' Vy' представляет собой и общеутвердительное силлогистическое суждение A xy - “Всякое x есть y ” . Дополнением A xy в УА является частноотрицательное суждение Oxy ¬Axy Vxy' Vx' Vy , а инверсией термина y получаются общеотрицательное ExyAxy' Vx V'xyVy и частноутвердительное Ixy Oxy'VxyVx'Vy' . Именно в УА законы подчинения частных посылок общим совместимы с силлогистическим законом исключенного третьего и имеет место треугольник противоположностей Васильева:
Axy ν Exy ν ¬Axy¬Exy Axy ν Exy ν OxyIxy 1 .

Непарадоксальная “строгая импликация”, аксиоматику которой вводил Льюис, а также Аккерман, представима в алгебре 1-й ступени как общий атрибут элементов совокупности, определяющей аристотелево следование, выражение которой предварительно преобразовано к виду
VxyV'xy'Vx'y'. Искомая импликация оказывается трехзначной функцией двухзначных терминов: x —>y xy ν σx'y ν x'y'. Но она, как и ее двухзначный прототип, не может быть характеристической функцией отношения следования, адекватно неотобразимого средствами 1-й ступени.

Ситуация в логике убедительно свидетельствует о том, что и в трех соснах, когда видят два, глядя на три, блуждать можно без конца, причем блуждать научно и изобретательно - виртуальные миры неисчерпаемы и неисчислимы. Но ведь мы живем в единственном реальном мире, и Органон должен упреждать заблуждения в познании и благоустройстве именно этого мира, нашего бытия. Так понималось назначение информатики Аристотелем и его достойными последователями. Логики уклонились от этой цели, и теперь информатика при всей ее технической мощи и “искусственном интеллекте” функции Органона не выполняет. Она не предоставляет нам безупречных методов и инструментов рассуждения, вынуждая полагаться на эмпирику и интуицию, ее положения оказываются неадекватными реальности, несовместимыми со здравым смыслом, с диалектикой. Очевидна, однако, возможность коренного исправления ситуации: ведь не извращенная двухзначниками силлогистика Аристотеля с законом сосуществования противоположностей и с привходящим в качестве третьего-среднего есть та самая диалектическая логика , которую днем с огнем ищут современные мудрецы.

Литература

1. Аристотель. Сочинения в четырех томах. - М.: "Мысль", т.1 - 1975, т.2 - 1978.
2. Брусенцов Н.П. Искусство достоверного рассуждения. Неформальная реконструкция аристотелевой силлогистики и булевой математики мысли. - М.: Фонд "Новое тысячелетие", 1998.
3. Брусенцов Н.П., Жоголев Е.А., Маслов С.П., Рамиль Альварес Х. Опыт создания троичных цифровых машин // Компьютеры в Европе. Прошлое , настоящее и будущее . - Киев , " Феникс ", 1998. С . 67-71.
4. Brusentsov N.P., Vladimirova Yu.S. Solution of Boolean Equations // Computational mathematics and modeling, V ol.9, No 4, 1998, pp.287-295.
5. Васильев Н.И. Воображаемая логика. Избранные труды. - М.: "Наука,, 1989.
6. Карпенко А.С. Многозначные логики // Логика и компьютер. Вып.4. - М.: "Наука", 1997.
7. Кэррол Льюис. Символическая логика // Льюис Кэррол. История с узелками. - М.: "Мир", 1973.
8. Лукасевич Я. Аристотелевская силлогистика с точки зрения современной формальной логики. - М.: ИЛ, 1959.
9. Пиаже Ж. Логика и психология // Избранные психологические труды. - М.: "Просвещение", 1969.
10. Порецкий П.С. О способах решения логических равенств и об обратном способе математической логики. - Казань, 1884.
11. Слинин Я.А. Современная модальная логика. - Л.: Изд-во Ленингр. ун-та, 1976.
12. Стяжкин Н.И. Формирование математической логики. - М.: "Наука", 1967.
13. Отчеты по НИР "Развитие конструктно-ориентированного подхода к информатике и компьютерной дидактике" (№ гос. рег. 01.960.009505). - ВНТИЦ, инв. №№ 02.9.80 003626, 02 .9.80 005206, 02.20.0000209.

Заметки о трехзначной логике
Доложено на Ломоносовских чтениях 24 апреля 2000 г. на факультете ВМиК МГУ.

Опубликовано: Москва, SvR - Аргус, 2000, с. 16 и в сборнике "Программные системы и инструменты", труды ф-та ВМиК МГУ, №1, Москва: МАКС Пресс, 2000, с. 13-23.
Помещено в музей 16.04.2007 с разрешения автора, по тексту с сайта http://ternarycomp.narod.ru/