Введение в недоопределенность

А.С. Нариньяни

2. Основные понятия

В предыдущей главе мы выяснили два основных различия Н-математики от привычной традиционной:

• Традиционная вычислительная математика решает задачи на основе алгоритмического подхода, а Н-матемика оперирует моделями;
• Понятие переменной в Н-математике принципиально отличается от традиционной классической переменной.

Соотношением алгоритма и модели мы займемся специально в главе 3, а в данной главе доопределим Н-переменную и введем понятия Н-расширения, Н-операции и Н-отношения.

2.1. Н-переменная и Н-расширение

В п.1.2 мы сравнили два основных понятия переменной — алгоритмической и классической. Первая в общем случае не имеет прямого отношения к параметрам объекта расчетов, но может менять значение в ходе процесса вычислений. Вторая наоборот, прямо соответствует параметру объекта, но получать значение может один раз — в результате решения задачи.

Мы уже убедились, что Н-переменная содержательно принципиально отличается и от той и от другой. С одной стороны, Н-переменная, как и классическая, ставится в соответствие конкретному параметру объекта моделирования. С другой, ее недоопределенное значение в общем случае уточняется, т.е. меняется, в ходе решения. Это радикально изменяет сам аппарат ее использования в процессе вычисления.

Так что введение основных понятий Н-математики придется начать с завершения рассмотрения особого содержания Н-переменной, которое отражается не только на области ее значений, но и на ее прагматике.

Выше уже упоминалось, что в Н-математике выражения *х = *а₁(где *х это Н-переменная, а *а₁ - ее Н-значение) получает следующий смысл: значение переменной х, представленной Н-переменной *х, принадлежит подобласти значений х, представленной Н-значением *а₁.

При этом в процессе Н-вычислений ключевую роль играет операция присваивания : при *х = *а₁присвоение *х:= *а₂интерпретируется следующим образом : значение х принадлежит как подобласти *а₁, так и подобласти *а₂, т.е. результат присвоения таким образом принадлежит одновременно обоим этим областям и определяется, следовательно, как *х = *а₁∩ *а₂. Например, для Н-чисел, представленных интервалами, это выглядит следующим образом:

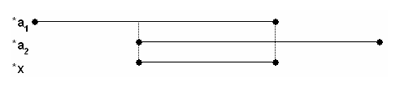
или верхняя граница нового значения *x равна min верхних границ *а₁ и *а₂, а нижняя граница нового значения *x равна max нижних границ *а₁ и *а₂.

Очевидно, что если интервалы не пересекаются, то по приведенным выше формулам получим результирующий интервал, в котором нижняя граница больше правой, т.е. противоречие, — что говорит об отсутствии решения.

Операция присваивания для Н-переменных является ключевым компонентом аппарата Н-моделей, обеспечивающим процесс решения таким образом, что в его рамках любая Н-переменная может только уточняться и весь процесс стягивания k -мерного пространства является монотонным.

2.2. Н-операция и Н-отношение

Возможность оперировать с Н-переменными относится не только к вычислительной алгебре и параметрам-числам. Любой формальной системе можно сопоставить ее недоопределённое расширение (Н-расширение) , которое включает как соответствующий тип Н-переменной (логический для алгебры логики, множества для теории множеств, и т.п.), так и соответствующее расширение операций (Н-операции) и отношений (Н-отношения) исходной формальной системы.

Каждой k -местной операции f  над обычными значениями a₁ ,..., , a_k, принадлежащими соответственно областям A₁,..., A_k:

f: A₁,..., , A_k →A_k+1,

сопоставим ее Н-расширение над соответствующими Н-значениями (Н-операция и Н-переменные далее, как и выше, отмечаются звездочкой):

*f: *A₁,...,*A_k → *A_k+1,

результат которой для любого набора Н-значений * a₁,...,* a k определяется как множество значений операции f для всех возможных наборов значений a₁ ,..., a_k, принадлежащих Декартову произведению *a₁x ... x*a_k. Т.е.

*f (* a₁ ,...,* a_k) = {f ( a₁ ,..., a_k) | a_i ∈* a_i, i = 1,..., k}.

Например, Н-расширению операции x : = z  — у над Н-значениями *y = {7, 8,} и *z = {12, 13, 14} соответствует Н-операция вычитания, комбинирующая все значения *y и *z и дающая в результате значение *x = {4, 5, 6, 7}.

Поскольку Н-математика оперирует с моделями, а они, как уже было сказано выше, представляют собой системы отношений, связывающих множество параметров (т.е. Н-переменных) данной задачи, то нам необходимо также познакомиться с Н-расширениями отношений.

Как уже упоминалось, в сякое отношение r (а₁,...,а_k) определяет некоторое подмножество Декартова произведения областей значений A₁ х...х A_k. Оно может интерпретироваться набором функций а_i=f_i(а₁,..., а_i-1, а_i+1,...,а_k), отображающих подмножество r (а₁, ... , а_k) на области значений каждой из переменных а₁,..., а_k.

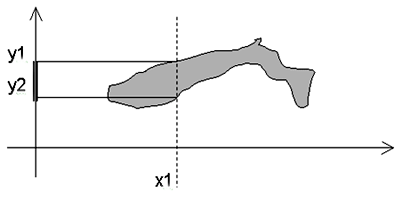
На этой иллюстрации тело отношения r(x,y) интерпретируется функций y= f'(x), сопоставляющей каждому х1 в общем случае интервал [у2, у1]. Аналогична и вторая функция интерпретации x=f''(y). Для отношений, определенных в символьном виде — например, уравнений — функции интерпретации определяются эквивалентными выражениями, представляющими каждую переменную явно через остальные.

Например, уравнению x + y  — z = 0  соответствуют три функции интерпретации:

z: = x+y; x: = z-y; y: = z-x;

Таким образом, Н-отношение

*r (*x₁,...,*x_k) интерпретируется k Н-функциями

*x_i = *F_i(*x₁,...,*x_i-1, *x_i+1,..., *x_k) i = 1,..., k ,

где каждая Н-функция *F_i (*x₁,...,*x_i-1, *x_i+1,...,*x_k) реализует Н- операцию *f_i (*а₁,...,*а_i-1, *а_i+1,...,*а_k), при всех *x_j = *а_j. Если значение числовой Н-переменной *x представлять интервалом [x_-, x^-] , где x_- — минимум, а x^-- максимум Н- значения *x , то уравнение нашего примера

x + y - z = 0 

будет интерпретироваться шестью функциями интервальной алгебры [20]:

z^-: = x^-+y^-;
z_-: = x_-+y_-;
x^-: = z^- - y_-;
x_-: = z_- - y^-;
y^-: = z^- - x_-;
y_-: = z_- - x^-;

Недоопределенность и Н-модели | Оглавление | Иллюстративный пример

Перепечатывается с разрешения автора
Статья помещена в музей 29.09.2008 года