Введение в недоопределенность

А.С. Нариньяни

3. Иллюстративный пример

3.1. K-мерное пространство модели

Напомним, что множеству А параметров-переменных модели, состоящему из k  элементов, соответствует k -мерное пространство, являющееся декартовым произведением областей значений всех переменных данного множества А. Точки этого пространства отображают все k -мерные наборы значений всех переменных А. Соответственно, каждая модель определяет в пространстве значений своих параметров некоторое тело — область решений — образованное точками, удовлетворяющими всем отношениям данной модели.

Если модель полностью определена, ее область решений состоит из единственной точки. Если она противоречива, область решений пуста. И, наконец, в общем случае, при недоопределенной системе отношений она содержит множество точек или целые гипертела. Проекции области решений на каждый из параметров задают их области значений для данной модели.

Добавление к модели М любого дополнительного ограничения определяет модель М', область решений которой, как очевидно, вложена в область решений исходной модели М. Соответственно, области значений части или всех параметров внутри М' в общем случае уже, чем внутри М. 

Если ограничение задается сужением области значений какого-либо из параметров, то из области решений модели убираются части, проекция которых попадает в исключенную зону значений данного параметра. Например, при задании ограничения, сужающего интервал значений числовой переменной изменением одной из его границ, от области решений исключаемая часть отсекается (k-1)-мерной гиперплоскостью, проходящей через новую границу интервала. Подобные ограничения являются типичными для многих приложений, представляя, например, технические требования для трансформатора или финансовые условия для инвестиционного проекта.

Следует отметить, что наиболее простой формой отражения k -мерного подпространства является k -мерный параллелепипед A₁ х...х A_k, где А_i — проекция области решения на область значений переменной х_i. На рисунке такой параллелепипед изображен в двухмерной проекции.

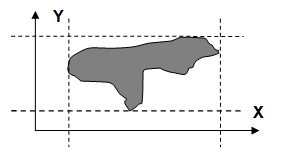
Рис. Параллелепипед области решения: отображение в двухмерной проекции.

Конечно, такой параллелепипед дает достаточно грубое отображение области решения, но другого простого и наглядного способа отображение области решения для k  больше двух нет, да и тот годиться только для моделей с числовыми параметрами, представляемыми интервалами.

Поскольку модель может включать унарные ограничения относительно некоторых отдельных переменных, то эти ограничения определяют в явной форме начальное K -мерное подпространство, включающее область решений данной модели.

Н-математика реализует для каждой модели универсальный вычислительный процесс, сжимающий начальное подпространство до k -мерного параллелепипеда, содержащего все множество решений. Ниже мы рассмотрим пример вычислительного процесса, порождаемого Н-моделью алгебраического типа.

3.2. Пример

Рассмотрим теперь простой пример, иллюстрирующий используемый в Н-моделях процесс вывода. Пусть требуется найти решение системы из двух линейных уравнений с двумя неизвестными:

F₁: y=x-1; F₂: 4х+3y = 12. 

Графики этих уравнений изображены на рис.2.

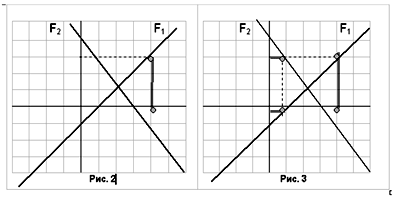
Каждое из этих уравнений можно рассматривать как неявную функцию от переменных x  и y . Предположим, что известна начальная оценка значения переменной x < 4. Идея недоопределенных вычислений состоит в том, что по текущей оценке поочередно вычисляются проекции функций F₁ и F₂ на x и y. Например, проекция F₁ на y для x = 4 равняется 3 (Рис. 2).

Теперь, если для y = 3 вычислять проекцию F₂ на x, то получим значение x  = 0.75, а F₁при этом значении х определяет у = -0.25. Результат такой проекции изображен на Рис.3. В свою очередь F₂ при этом значении у определяет х = 3.0625 (см. Рис. 4).

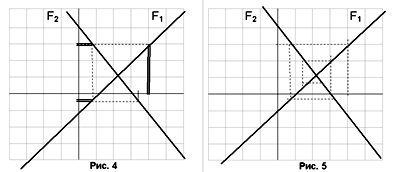
Продолжая этот процесс, мы шаг за шагом по спирали автоматически приближаемся к искомому решению — Рис. 5. 

Очевидно, что начальное ограничение x < 4 порождает две спирали — одна от подстановки x = 4 в F₁ и другая — в F₂. Таким образом, ограничение х = [а1, а2] порождает четыре спирали, а добавление к нему ограничения у = [в1, в2] доводит число спиралей до восьми, причем они взаимодействуют: часть их закручивается, как рассмотренная, другие — раскручиваются (при этом раскручивание автоматически блокируется механизмом, обеспечивающим монотонность процесса общего стягивания — см. главу 5).

Напомним, что параметры реальных задач всегда имеют начальные оценки границ их значений. Это имеет место даже в тех случаях, когда исходные ограничения на область значений того или иного числового параметра не заданы явно, поскольку оценка значения от минус до плюс бесконечности всегда представляются в машине двумя конкретными числами — максимальными положительным и отрицательным значениями числа в данном компьютере.

Таким образом, для k  интервальных Н-переменных всегда одновременно будут параллельно реализоваться 4k  спиралей, которые сообща монотонно (в общем случае, 2k закручивающихся точек) стягиваются к одному и тому же результату, независимо от порядка выполнения соответствующих шагов.

В рассмотренном примере система имела одно решение. Однако в сложных задачах решений может быть несколько или даже много, — в последнем случае они могут образовывать область решений или систему таких областей в K-мерном пространстве модели. При этом процесс решения будет сужать k -мерный параллепипед, охватывающий соответствующую систему областей.

Основные понятия | Оглавление | Модель vs. алгоритм

Перепечатывается с разрешения автора
Статья помещена в музей 30.09.2008 года