Введение в недоопределенность

А.С. Нариньяни

Вычислительные Н-модели

Ниже дается более детальное определение Н-модели и соответствующего процесса вычислений.

6.1. Определения

Поскольку понятие Н-модель пока не определялось формально, то на данном этапе сделать это необходимо. Н-модель M = (V, R, W, C) состоит из следующих четырех множеств:

V – множество параметров из заданной предметной области,
R – множество ограничений на значениях параметров из V,
W – множество функций присваивания, и
C – множество функций проверки корректности.

При этом каждому параметру v_i ∈V сопоставлены:

•  Область Н-значений V_i;

•  начальное Н-значение из V_i;

•  функция присваивания W_i;

•  функция проверки корректности C_i;.

Функция пр­исваивания — это двухместная операция, работающая при каждой по­пытке присваивания очередного Н-значения параметру v_i и определяющая новое Н-значение параметра как функцию от текущего и присваиваемого Н-значений (обычно в качестве такой функции используется операция пересечения этих Н-значений).

Функция проверки корректности — это унарный предикат, вычисляемый при каждом изменении Н-значения параметра х и проверяющий правильность его нового Н-значения.

Ограничения из R должны быть функционально интерпретируемыми.

На уровне интерпретации Н-модель представляется двудольным ориентированным графом, в котором выделены два типа вершин: параметры и функции интерпретации отношений. Дуги связывают вершины-фун­кции и вершины-параметры. Входящие в вершину-функцию F дуги соотносят с ней параметры, значения которых выступают в качестве входных аргументов для функции F, исходящие — указывают на параметры, в которые должна производиться запись вырабатываемых функцией F результатов.

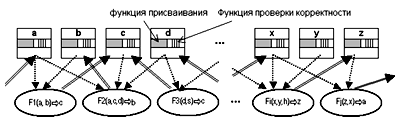
Каждой вершине-параметру сопоставляются тип, значение, функции присваивания и проверки корректности.

6.2. Процесс удовлетворения ограничений для Н-модели

Процесс вычислений для Н-модели имеет потоковый характер, - изменение значений вершин-параметров сети активирует (вызывает к исполнению) все функциональные вершины, для которых эти параметры являются входными аргументами, а исполнение функциональ­ных вершин в свою очередь может вызывать изменение значений результирующих параметров. Вычисления заканчиваются тогда, когда либо не останется активных функциональных вершин (результат - УСПЕХ )‚ либо функция проверки корректности вырабатывает значение ошибка (результат - НЕУДАЧА ).

Как было сказано выше, в Н-моделях вместо обычных переменных V рассматриваются их недоопределенные расширения * V . При этом функции присваивания производят пересе­че­ние текущего и присваиваемого Н-значений, а функции проверки корректности – проверяют, не являются ли пус­тыми или некорректными новые Н-значения.

В работе [23] доказаны следующие утверждения:

(i) Процесс удовлетворения ограничений в Н-моделях за­ве­рша­ет­ся за ко­нечное число шагов.

(ii) В случае УСПЕХА процесса, решение задачи (если оно существует) лежит внутри полученного процессом результата (декартова произведения Н-значений).

(iii) Результаты процесса определяются только начальными Н-значениями параметров модели и не зависят от конкретного порядка выбора оче­ре­дно­го ограничения для его интер­пре­тации. Это относится как к завершениям НЕУДАЧА или УСПЕХ, так и – в случае УСПЕХА – ко всем результирующим Н-значениям параметров модели в рамках указанной для них точности.

В данном случае важно, что в отличие от алгоритмического понятия эквивалентности по результату , имеющего в виду совпадение ответов, данная выше формулировка р езультаты процесса не зависят от конкретного порядка подразумевает, что результаты равны с заданной точностью. Такая эквивалентность характерна для недетерминированных процессов вычислений.

6.3. Пример работы процесса

В главе 3 мы рассмотрели процесс вычислений для Н-модели на наглядной графической иллюстрации. Ниже работа такого процесса будет рассмотрена детально на примере достаточно простой системы из двух линейных уравнений с двумя целочисленными неизвестными:

	x + y =12;	(2)
	2 * x = y;

Предположим, что значения x и y ограничены следующими неравен­ствами:

0 ≤x ≤ 100; 0 ≤ y ≤ 100. (3)

Таким образом, множество параметров V данной модели содержит две целочисленные пере­мен­ные x и y , множество ограничений R — два уравнения и четыре неравенства.

Для создания соответствующей Н-модели требуется выбрать некоторый вид Н-расширения целого числа, которое может быть различным. Пусть в данном случае целое Н-число будет представлено для простоты прослеживания процесса Н-расширением интервал (хотя, как уже отмечалось, это расширение не является единственно возможным, - им может быть, например, и список значений Н-числа).

Как мы видели в п.2.1, функция присваивания W i изменяет значение Н-числа v_i таким образом, что его нижняя граница может только увеличиваться, а верхняя ? только уменьшаться. Функция проверки корректности C i проверяет, чтобы нижняя граница Н-числа v i не превосходила верхнюю. Операции для интервальных Н-чисел определяются в соответствии с правилами интервальной математики [20].

Так как множество V содержит две переменные типа Н-число, множество функций присваивания (W) и множество функций проверки корректности (C) содержат по два элемента: W = {Wx , Wy}; C = {Cx, Cy};

Множество функций интерпретации уравнений (2) состоит из четырех элементов ( f₁ – f₄):

f₁: y → 12–x; f₂: x → 12–y;

f₃: y → 2x; f₄: x → y/2;

Согласно правилам интервальной арифметики, семантика функций интерпретации ( f 1   –  f 4   ) представляется следующим образом:

f₁: [y_- , y^-] →[12–x^-, 12 – x_-];
f₂: [ x_-, x^-] →[12–y^-, 12–y_-];
f₃: [y_-, y^-]→ [min {2*x_-, 2*x^-}, max {2*x_-, 2*x^-}];
f₄: [x_-, x^-] → [min {y_-/2, y^-/ 2 }, max {y_-/2, y^-/ 2 }];

Ограничения (3) можно проинтерпр­етировать на этапе генерации Н-сети, и тогда нижние и верхние границы x и y станут равными 0 и 100 соответственно. Таким образом, на первом шаге процесса потоковых вычислений имеем

x = [0,100]; y = [0,100];

В табл. 1 приведена последовательность шагов потокового процесса для данной задачи. В таблице предполагается, что на каждом шаге исполняется первая функция из множества активных функций (она отделена от остальных символом ‘|'). Как уже говорилось, порядок применения функций может быть произвольный, в данном случае выбран данный конкретный для простоты рассмотрения примера.

На первом шаге итерации исполняется функция f₁. В результате работы этой функции получаем значение y = [–88, 12]. После этого вызывается функция присваивания Wy. Текущее значение y равно [0, 100], новое ¾ [–88, 12]. Функция присваивания вырабатывает значение [0, 12] и присваивает его y . Присвоение нового значения отмечается флагом «Да», в результате чего вызывается функция проверки корректности Cy. Условие корректности для y (0 ≤ 12 ) не нарушается, и процесс исполнения Н-модели продолжается.

Таблица 1. Протокол исполнения Н-модели

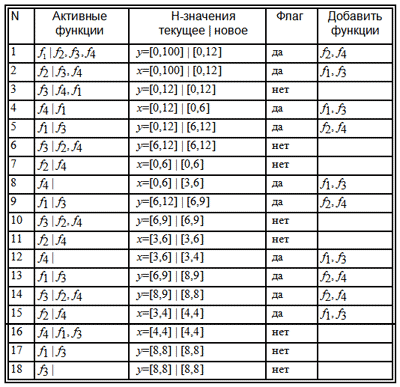
Как видим, у переменной y изменилась только верхняя граница (так как новая нижняя граница (–88) меньше текущей (0)). Поскольку условие корректности для y здесь не нарушается, то происходит активация функций интерпретации f₂ и f₄, для которых y является входным аргументом. Ввиду того, что эти функции уже входят в множество активных функций, их повторная активация не происходит. Далее исполняется следующая функция ( f₂) из очереди.

Вычисления заканчиваются тогда, когда нижняя и верхняя границы как x , так и y становятся равными друг другу. Это произойдет при значениях x - и x - равными 4, а y - и y - ¾ равными 8. При таких значениях исполнение любой функции f₁– f₄ не изменяет значения своего результата и множество активных функций становится пустым.

Свойства недоопределенных расширений | Оглавление | Примеры использования Н-моделей

Перепечатывается с разрешения автора
Статья помещена в музей 02.10.2008 года