Введение в недоопределенность
А.С. Нариньяни
Примеры использования Н-моделей
Так как процесс вычислений в Н-моделях является универсальным, т.е. не зависит от типа задачи, аппарат Н-моделей используется для решения не только численных, но и задач из других предметных областей. Н-модели могут достаточно просто настраиваться на любые области. Для этого необходимо определить типы Н-данных и ограничений, характерных для той или иной предметной области. При этом, в отличие от других решателей, Н-модели могут использоваться для решения так называемых смешанных задач, содержащие как численные (вещественные и целые) переменные, так и множества, перечисления, дискретные параметры и т.п.
Ввиду ограниченного объема статьи ниже рассмотрим только относительно небольшие примеры, показывающие основные возможности аппарата Н-моделей.
7.1. Решение комбинаторных задач
Комбинаторные задачи представляют собой предмет интенсивных исследований в области искусственного интеллекта. Сложность решения таких задач объясняется огромным пространством поиска при относительно малом количестве вычислений. Постоянно изобретаются все новые и новые эвристики, позволяющие сократить пространство поиска и находить решение за приемлемое время. Н-модели, за счет использования Н-значений вместо точных значений многие комбинаторные задачи могут эффективно решать и без привлечения такого рода эвристик.
Классическим примером комбинаторной задачи являются буквенно-арифметические головоломки. Одна из таких головоломок представляет собой известную шутливую телеграмму: SEND + MORE = MONEY . Предполагается, что слова в этой телеграмме представляют собой зашифрованные десятичные записи натуральных чисел, в которых каждая буква обозначает цифру от 0 до 9. При этом разные буквы обозначают разные цифры, а старшие разряды чисел (обозначенные в данном примере буквами S и M ) не равны нулю. Необходимо найти такую подстановку цифр вместо букв, при которой сумма двух первых зашифрованных чисел равна третьему:

За простотой формулировки здесь скрывается трудоемкость решения: действуя простым перебором, мы должны рассмотреть максимум 8! = 40320 вариантов различных подстановок.
Для того, чтобы решить такую задачу с использованием аппарата Н-моделей необходимо сопоставить каждой букве Н-значение - в данном случае множество, содержащее все цифры от 0 до 9. Кроме букв в Н-модели должны присутствовать переносы из одного столбца в другой. Их Н-значения равны множеству {0, 1}. Ограничения представляются в виде линейных целочисленных уравнений, связывающих буквы из одного и того же столбца (с учетом переносов):
S + M + c3 = O + 10*c4;
E + O + c2 = N + 10*c3;
N + R + c1 = E + 10*c2;
D + E + 0 = Y + 10*c1;
alldiff(S, E, N, D, M, O, R, Y);
Последнее ограничение означает, что значения всех букв должны быть различными. Заметим, что во втором и третьем столбцах уравнения выглядят (упрощенно) как E + O = N и N + R = E. С учетом соответствующих переносов сумма этих уравнений выглядит следующим образом:
O + R + c 1 = 9*c2 + 10*c 3;
Эта задача может быть описана различным образом, например, еще и так:
(D+10*N+100*E+1000*S)+
(E+10*R+100*O+1000*M) = Y+10*E+100*N+1000*O+10000*M;
alldiff( S, E, N, D, M, O, R, Y );
Описанный выше процесс удовлетворения ограничений за небольшое число шагов находит следующее решение:
S = 9; E = 5; N = 6; D = 7; M = 1; O = 0; R = 8; Y = 2; c1 = 1; c2 = 1; c3 = 0; c4 = 1.
7.2. Решение теоретико-множественных задач
Множества являются одним из наиболее интересных для приложений нечисловых типов данных. Впервые понятие недоопределенного множества было предложено в работе [10]. Существует несколько различных способов представления недоопределенного множества, ниже мы используем способ, предложенный в [10].
Недоопределенное множество A представляется тремя компонентами:
A = <A+, A–, M > ,
где A+– множество элементов, которые точно принадлежат А;
A–– множество элементов, которые точно не принадлежат А;
М – мощность множества А , представленная недоопределенным целым числом.
Естественно, что количество элементов в A+и A–может только возрастать. Если обозначить через U – все потенциальные элементы (универсум) множества А, а через card ( A ) – мощность множества A , то справедливы следующие ограничения:
М ≥card(A+) ; М≤card(U) – card(A– );
A+![]() U; A–
U; A–![]() U; A+∩A–= ∅;
U; A+∩A–= ∅;
Рассмотрим один простой пример. Предположим, что в универсуме, состоящем из 20 букв (от а до t ), имеются 4 множества ( A, B, C и D ) со следующими значениями:
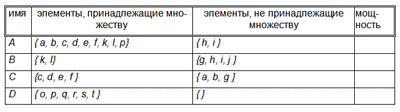
Также предположим, что модель состоит из следующих ограничений:
C = A\B; D ![]() C; card(A)≤14; card(B) > 5;
C; card(A)≤14; card(B) > 5;
После применения к данной Н-модели процесса удовлетворения ограничений, получаем следующий результат:
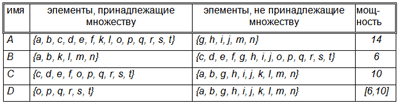
Таким образом, значения множеств A, B и C полностью уточнились. Значение множества D уточнилось, но не полностью: при текущих ограничениях остается неясным, принадлежат ли множеству D элементы c, d, e и f.
7.3. Решение смешанных задач
Основное преимущество Н-моделей состоит в том, что они способны решить задачи, которые не могут быть решены никаким другим способом кроме полного перебора, в тех случаях, когда перебор возможен. Это относится в первую очередь к так называемым смешанным задачам: когда в модели присутствуют переменные и ограничения самой различной природы (численные, дискретные, множественные, таблицы и т.п.).
Предположим, что к Н-модели из предыдущего раздела добавляются следующие два уравнения, неравенство и логическая импликация над вещественными (x, y), целым (k) и множествами (D, A, C):
x2 + 6*x = y-2k;
k*x + 7.7*y = 2.4;
k < 3;
(x < 2.5*y) & (D ⊂ A) → (k*y ≤ 3) & (k > y + 1) & (C ![]() D).
D).
В такой модели результат будет следующим:

Важно отметить, что хотя понятие Н-расширения применимо к любой формальной системе, а приведенных выше примеров достаточно, чтобы продемонстрировать возможность использования недоопределенности в отношении самых различных типов данных, пока основной областью приложения остается вычислительная алгебра и интервал в качестве Н-значения для чисел.
Вычислительные Н-модели | Оглавление | Роль интервала и другие НЕ-факторы
Перепечатывается с разрешения автора
Статья помещена в музей 03.10.2008 года
